Уравнение Ва-дер-вальса

Ван-дер-Ваальсом в уравнение Клапейрона — Менделеева введены две поправки.

1. Учет собств-о объема молекул. Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактич своб объем, в котором могут двигаться молекулы реал газа, будет не V m, а V m — b, где b — объем, занимаемый самими молекулами.

Объем b равен учетверенному собственному объему молекул. Если, например, в сосуде находятся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние, меньшее диаметра d молекулы. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса d, т. е. объем, равный восьми объемам молекулы или учетверенному объему молекулы в рас­чете на одну молекулу.

2. Учет притяжения молекул. Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислени­ям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату моляр­ного объема, т. е. где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного при­тяжения, V m — молярный объем.

Вводя эти поправки, получим уравнение Ван-дер-Ваальса для моля газа (уравнение состояния реальных газов):

Для произвольного количества вещества v газа (v=m/M) с учетом того, что V=vV m, уравнение Ван-дер-Ваальса примет вид

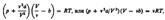
где поправки а и b — постоянные для каждого газа величины, определяемые опытным путем (записываются уравнения Ван-дер-Ваальса для двух известных из опыта состоя­ний газа и решаются относительно а и b). Объём молекул и силы между ними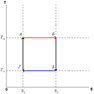

Цикл Карно — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Состоит из 2 адиабатических и 2 изотермических процессов.

Свойство цикла Карно: он может быть проведён как в прямом, так и в обратном направ-и, при этом энтропия адиабатически изолированной (без теплообмена с окружающей средой) системы не меняется.

Пусть тепловая машина состоит из нагревателя с температурой , холодильника с температурой и рабочего тела.

Цикл Карно состоит из четырёх стадий:

• Изотермическое расшир-е (на рисунке — процесс A→ Б). В начале процесса рабочее тело имеет температуру , то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты . При этом объём рабочего тела увеличивается.

• Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс Б→ В). Рабочее тело

отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.

• Изотермическое сжатие (на рисунке — процесс В→ Г). Рабочее тело, имеющее к тому времени температуру , приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты .

• Адиабатическое (изоэнтропическое) сжатие (на

При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия:

при .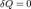

Поэтому цикл Карно удобно представить в координатах T и S (температура и энтропия).

[править]

КПД тепловой машины Карно

Кол-во теплоты, получ рабочим телом от нагревателя при изотермическом расширении, равно

.

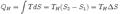при изотермическом сжатии рабочее тело отдало холодильнику

.

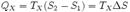Отсюда коэффициент полезного действия тепловой машины Карно равен

.

Из посл выр видно, что КПД тепловой машины Карно зависит только от температур нагревателя и холодильника. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.

Поэтому максимальный КПД любой тепловой машины будет меньше или равен КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника.

Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплоты δ Q, полученного телом, к соответствующему приращению его температуры δ T:

Единица измерения теплоёмкости в системе СИ — Дж/К.

теплоемкость при постоянном давлении всегда больше теплоемкости при постоянном объеме. Их отношение равно

где γ — показатель адиабаты (коэффициент Пуассона).