
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Умножь на 3
|
|
Прибавь 1
умножь на 3
Первая из них увеличивает число на экране на 1, вторая – утраивает его.
Программа для Утроителя – это последовательность команд.
Сколько есть программ, которые число 1 преобразуют в число 20?
Решение (1 способ, составление таблицы):
1) заметим, что при выполнении любой из команд число увеличивается (не может уменьшаться)
2) начнем с простых случаев, с которых будем начинать вычисления: для чисел 1 и 2, меньших, чем 3, существует только одна программа, состоящая только из команд сложения; если через 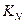 обозначить количество разных программ для получения числа N из 1, то
обозначить количество разных программ для получения числа N из 1, то 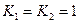 .
.
3) теперь рассмотрим общий случай, чтобы построить рекуррентную формулу, связывающую 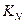 с предыдущими элементами последовательности
с предыдущими элементами последовательности 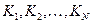 , то есть с решениями таких же задач для меньших N
, то есть с решениями таких же задач для меньших N
4) если число N не делится на 3, то оно могло быть получено только последней операцией сложения, поэтому 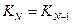
5) если N делится на 3, то последней командой может быть как сложение, так и умножение
6) поэтому для получения 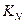 нужно сложить
нужно сложить 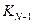 (количество программ с последней командой сложения) и
(количество программ с последней командой сложения) и 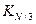 (количество программ с последней командой умножения). В итоге получаем:
(количество программ с последней командой умножения). В итоге получаем:
если N не делится на 3: 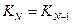
если N делится на 3: 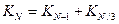
7) остается заполнить таблицу для всех значений от 1 до N:
| N | ||||||||||||||||||||
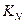
|
8) Заметим, что количество вариантов меняется только в тех столбцах, где N делится на 3, поэтому из всей таблицы можно оставить только эти столбцы:
| N | ||||||||
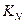
|
9) заданное число 20 попадает в последний интервал (от 18 до 21), поэтому …
10) ответ – 12.
Решение (2 способ, подстановка – вычисления по формулам «с конца»):
1) п. 1-6 выполняются так же, как и при первом способе; главная задача – получить рекуррентную формулу:
если N не делится на 3: 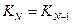
если N делится на 3: 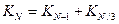
с начальными условиями 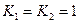
2) начинаем с заданного конечного числа 20; применяем первую формулу (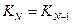 ), пока не дойдем до числа, делящегося на 3 (это 18):
), пока не дойдем до числа, делящегося на 3 (это 18):

3) далее применяем вторую формулу (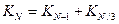 ):
):
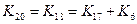
4) применяем первую формулу для 17:
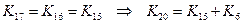
5) применяем вторую формулу для обоих слагаемых:
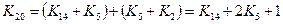
где учтено, что 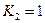
6) с помощью первой формулы переходим в правой части к числам, делящимся на 3:
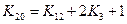
а затем применяем вторую формулу для каждого слагаемого
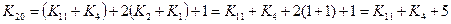
7) снова используем первую формулу
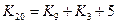
а затем – вторую:
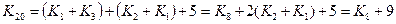
8) и еще раз
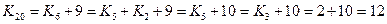
9) ответ – 12.
Решение (3 способ, О.В. Шецова, лицей № 6, г. Дубна):
1) будем составлять таблицу из трех столбцов: в первом записывается получаемое число от 1 до 20, во втором – какой последней командой может быть получено это число, а в третьем вычисляем количество различных программ для получения этого числа из 1
2) очевидно, что число 1 может быть получено с помощью одной единственной (пустой) программы:
| Число | Как можно получить? | Количество программ |
3) число 2 не делится на 3, поэтому его можно получить только командой сложения (+1), значит, количество программ для 2 совпадает с количеством программ для 1:
| Число | Как можно получить? | Количество программ |
| +1 | = 1 |
4) число 3 делится на 3, поэтому его можно получить с помощью двух команд: +1 (из 2) и *3 (из 1):
| Число | Как можно получить? | Количество программ |

|  1 1
| |
| +1 |  1 1
| |
| +1 *3 | 1 + 1 = 2 |
5) числа 4 и 5 не делятся на 3, поэтому их можно получить только с помощью команды +1, а число 6 может быть получено двумя командами:
| Число | Как можно получить? | Количество программ |
 +1 +1
|  1 1
| |
| +1 *3 |  1 + 1 = 2 1 + 1 = 2
| |
| +1 |  2 2
| |
| +1 |  2 2
| |
| +1 *3 | 2 + 1 = 3 |
6) следующая группа – 7, 8 (не делятся на 3) и 9 (делится на 3):
| Число | Как можно получить? | Количество программ |
| +1 | ||
 +1 *3 +1 *3
|  1 + 1 = 2 1 + 1 = 2
| |
| +1 | ||
| +1 | ||
| +1 *3 |    2 + 1 = 3 2 + 1 = 3
| |
| +1 | ||
| +1 | ||
| +1 *3 | 3 + 2 = 5 |
7) далее – 10, 11 и 12:
| Число | Как можно получить? | Количество программ |
| +1 | ||
| +1 *3 | 1 + 1 = 2 | |
 +1 +1
|  2 2
| |
| +1 | ||
| +1 *3 | 2 + 1 = 3 | |
| +1 | ||
| +1 | ||
| +1 *3 |  3 + 2 = 5 3 + 2 = 5
| |
| +1 |  5 5
| |
| +1 |  5 5
| |
| +1 *3 | 5 + 2 = 7 |
8) и так далее, вот полностью заполненная таблица (до конечного числа 20):
| Число | Как можно получить? | Количество программ |
| +1 | ||
| +1 *3 | 1 + 1 = 2 | |
| +1 | ||
 +1 +1
|  2 2
| |
 +1 *3 +1 *3
|  2 + 1 = 3 2 + 1 = 3
| |
| +1 | ||
| +1 | ||
| +1 *3 | 3 + 2 = 5 | |
| +1 | ||
| +1 | ||
| +1 *3 | 5 + 2 = 7 | |
| +1 | ||
| +1 | ||
| +1 *3 | 7 + 2 = 9 | |
| +1 | ||
| +1 | ||
| +1 *3 | 9 + 3 = 12 | |
| +1 | ||
| +1 |
9) ответ – количество программ, с помощью которых можно получить число 20 из 1, – считываем из последней ячейки третьего столбца
10) ответ – 12.
Решение (4 способ, М.В. Кузнецова и её ученики, г. Новокузнецк):
1) пусть 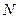 – искомое конечное число,
– искомое конечное число, 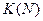 количества программ получения числа
количества программ получения числа 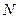
2) тогда для построения рекуррентной формулы определения 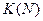 , нужно знать 2 факта:
, нужно знать 2 факта:
а) какой может быть последняя команда и сколько есть видов этого последнего действия?
б) для каждого «последнего» действия нужно знать число программ получения предыдущего числа, сумма этих количеств и есть искомое значение 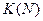 – число программ получения числа
– число программ получения числа 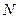 .
.
Например, общее количество программ получения числа 6 с помощью Утроителя равно 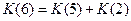 , т.к. есть ДВА способа завершения программ получения этого значения: 6=5+1 и 6=2∙ 3.
, т.к. есть ДВА способа завершения программ получения этого значения: 6=5+1 и 6=2∙ 3.
3) число программ получения числа 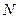 зависит от числа программ получения предыдущего значения, и что программы получения чисел, кратных 3-м могут завершаться 2-мя способами:
зависит от числа программ получения предыдущего значения, и что программы получения чисел, кратных 3-м могут завершаться 2-мя способами: 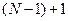 или
или 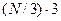 , а все остальные числа получают только первым способом:
, а все остальные числа получают только первым способом: 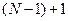 .
.
4) составим рекуррентную формулу для определения числа программ получения числа 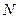 :
:
при 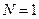 имеем
имеем 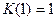
если 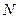 не кратно 3:
не кратно 3: 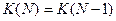
если 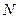 делится на 3:
делится на 3: 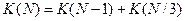
5) с помощью это формулы заполняем таблицу следующим образом:
– в первом столбце записываем все натуральные числа от 1 до заданного 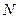 ;
;
– во втором столбце – числа, на единицу меньшие (из которых может быть получено 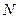 последней операцией сложения с 1);
последней операцией сложения с 1);
– в третьем столбце для чисел, кратных 3-м, записываем частное от деления числа, записанного в первом столбце, на 3 (из этого числа может быть получено 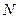 последней операцией умножения на 3);
последней операцией умножения на 3);
– в последнем столбце вычисляем 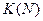 , складывая соответствующие значения для тех строк, номера которых записаны во втором и третьем столбцах:
, складывая соответствующие значения для тех строк, номера которых записаны во втором и третьем столбцах:
| N | N-1 | N/3 | K(N) |
 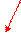 1 1
| – | ||
   2 2
| |||
| 1+1=2 | |||
 5 5
| |||
| 2+1=3 | |||
| 3 + 2=5 | |||
| 5 + 2 = 7 | |||
| 7 + 2 = 9 | |||
| 9+3 = 12 | |||
6) ответ – 12.
Решение (5 способ, А. Сидоров):
1) основная идея – число программ, преобразующих начальное число 1 в конечное 20 с помощью заданных в условии команд, равно числу программ, преобразующих конечное число 20 в начальное 1 с помощью обратных команд: «вычти 1» и «раздели на 3»
2) будем строить «обратное дерево» – дерево всех способов преобразования конечного числа в начальное; это лучше (в сравнении с построением «прямого» дерева, от начального числа к конечному), потому что операция умножения необратима – каждое число можно умножить на 3, но не каждое можно разделить на 3; из-за этого сразу отбрасываются тупиковые ветви, не дающие новых решений
3) рисуем сокращенное дерево, в котором черные стрелки показывают действие первой команды («прибавь 1»), а красные – действие второй команды («умножь на 3»); красные стрелки подходят только к тем числам, которые делятся на 3:
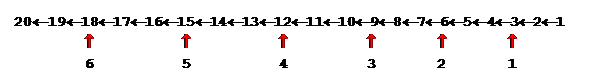
4) чтобы получить количество программ для каждого числа из верхней строки, нужно сложить соответствующие количества программ для всех чисел из нижнего ряда, которые не больше данного (программы с умножением), и добавить 1 (программа, состоящая из одних сложений)
5) очевидно, что для получения 1 существует одна (пустая) программа; тогда для числа 2 тоже получается одна программа, а для числа 3 – две программы:
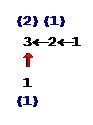
6) далее, для чисел 4 и 5 получаем 2 программы (после числа 3 нет «разветвлений» – подходящих красных стрелок), а для числа 6 – 3 программы, так как «подошло» еще одно разветвление (6 можно получить умножением 2 на 3), а для числа 2 мы уже подсчитали количество программ – оно равно 1:
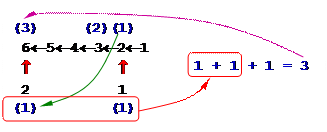
7) находить число программ для следующих чисел нам уже не понадобится, потому что при умножении на 3 они дают числа, большие, чем заданное конечное число 20
8) запишем полученные результаты в самой нижней строке для всех множителей от 1 до 6:
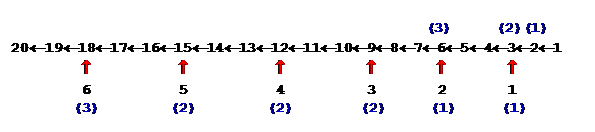
9) теперь остается сложить все числа в скобках в нижнем ряду (количество программ с командами умножения) и добавить 1 (одна программа, состоящая только из команд сложения):
3 + 2 + 2 + 2 + 1 + 1 + 1 = 12
10) ответ – 12.
Возможные проблемы:
· неверно определенные начальные условия
· неверно выведенная рекуррентная формула
· ошибки при заполнении таблицы (невнимательность)
· второй способ (подстановка), как правило, приводит к бОльшему количеству вычислений; конечно, можно отдельно выписывать все полученные ранее значения 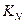 , но тогда мы фактически придем к табличному методу , но тогда мы фактически придем к табличному методу
|
Еще пример задания:
У исполнителя Калькулятор две команды, которым присвоены номера: