Задание № 3.

ЗАКОН РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Согласно третьему постулату метрологии из-за наличия случайных погрешностей результат измерения рассматривается как случайная величина.

Случайной называют величину, которая в результате опыта принимает значение заранее неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

В метрологии в ходе проведения измерений основное внимание уделяется закономерностям тех случайных явлений, которые обладают относительной устойчивостью некоторых свойств в их массовом проявлении. Такие случайные явления в массовом их проявлении в обыденной жизни встречаются довольно часто. Например, процент рождения мальчиков по отношению к общему числу рождения детей сохраняется довольно устойчиво (51, 5%). Устойчивы также средние значения таких случайных явлений, как рост людей, месячная температура в определенных районах и т.п.

Явления, рассматриваемые в теории вероятностей, называются событиями. Проведение отдельного наблюдения, опыта или измерения называют испытанием. Его результат называют также событием. События принято обозначать первыми прописными буквами латинского алфавита: А, В, С…

Примеры событий: а) появление при измерении положительной случайной погрешности; б) «появление герба», «появление цифры» при бросании монеты.

Событие называют случайным (возможным), если в результате данного испытания оно может произойти, а может и не произойти Примеры случайных событий: величина и знак случайной погрешности результата измерения какой-либо величины; выигрыш в Спортлото, попадание в цель при выстреле.

При большом числе испытаний, производимых в одинаковых условиях, обнаруживаются вполне устойчивые закономерности, что является основой при применении методов теории вероятностей и математической статистики к обработке массовых наблюдений.

Случайное событие может появиться в результате испытаний, которые могут быть повторены любое число раз при одних и тех же условиях. Такое событие называется массовым. Оно может быть охарактеризовано числом, подсчитав его частость 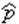или относительную частоту, выражающуюся отношением числа появлений этого события к числу всех произведенных испытаний, 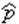=m/n. Например, произведено 20 измерений одной и той же величины, при этом положительных погрешностей оказалось 6. Следовательно, m=6, n=20, относительная частота появления положительной погрешности 6/20 = 0, 3 или 30%.

Относительная частота (частость) подсчитывается после опыта и выражается или дробью или в процентах.

Изучение массовых случайных событий показало, что при определенных условиях некоторые из них происходят с тем более постоянной устойчивой частостью, чем больше число испытаний. Появлением этих закономерностей является свойство устойчивости относительной частоты однородных случайных событий, т. е. уменьшение разброса ее значений, получаемых в равных сериях испытаний, при увеличении числа испытаний в каждой серии

Выполнив большую серию испытаний, можно с высокой точностью предсказать результат других таких же серий испытаний.

Английский ученый К. Пирсон, определяя относительную частоту появления герба при бросании монеты 12000 и 24000 раз, получил значения этой частоты соответственно 0, 5016 и 0, 5005. Нетрудно предсказать, что частость должна составлять значение, равное 0, 5.

При большом числе испытаний п относительная частота обнаруживает устойчивость, которая характеризует объективную связь между комплексом условий, в которых производится опыт, и событием.

С увеличением числа испытаний п в сериях колебания значений в разных сериях уменьшается, т. е. существует определенное значение относительной частоты, от которого она отклоняется в разных сериях испытаний в ту и другую сторону. Этой постоянной величиной является количественная мера степени объективной возможности появления события при одном опыте, называемая вероятностью события (р).

Вероятность р события А можно определить как отношение числа m случаев, благоприятствующих появлению события А, к числу п всех возможных случаев; при этом случаи предполагаются равновозможными, несовместными и единственно возможными.

.

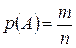Иногда

.

Из определения следует, что вероятность любого события А заключена между нулем и единицей

.

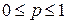Свойство относительной частоты – устойчивость. Впервые ее отразил
Я. Бернулли в виде теоремы. При числе испытаний п неограниченно большом с вероятностью, сколь угодно близкой к единице, относительная частота m/n события сколь угодно мало отличается от его вероятности в отдельном опыте.

Закон распределения вероятностей дискретной случайной величины, заданный в виде таблицы, называют рядом распределения. Для удобства восприятия ряда распределения строят графики. Для этого строят точки с координатами (xi, pi), а затем соединяют их отрезками. Полученная фигура называется многоугольником распределения или полигоном частот (рисунок 7).

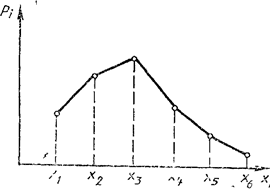
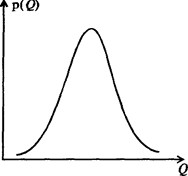
Рисунок 1 – Полигон частот и функция плотности распределения

Аналитически закон распределения задают обычно в виде функции и называют функцией распределения, которая является универсальной характеристикой случайной величины и существует для всех случайных величин – дискретных и непрерывных.

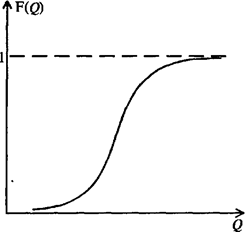
Функции распределения вероятности для дискретных и непрерывных (аналоговых) величин имеют вид, показанный на рисунке 2.

Наибольшее значение эмпирической функции распределения вероятности равно вероятности достоверного события, т.е. 1. Теоретическая функция распределения вероятности асимптотически приближается к единице.

Вероятность P того, что отдельный результат измерения окажется в интервале [x₁; x₂] равна площади криволинейной трапеции, ограниченной графиком плотности распределения вероятности p(x), осью абсцисс и перпендикулярами к ней на границах этого интервала (рисунок 3)

а) б)

Рисунок 2 – Функции распределения вероятности случайных величин:

а) дискретной б) непрерывной

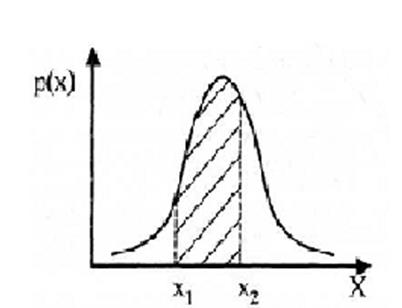
Рисунок 3 – Определение вероятности попадания отдельного значения

в заданный интервал по функции плотности распределения вероятности

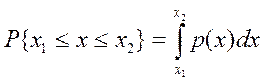
Функция распределения вероятностей случайной величины определят вероятность того, что случайная величина (отдельный результат измерения х) примет значение меньше ее аргумента. Следовательно, вероятность того, что результат измерения окажется в интервале [x₁; x₂], равна разности значений F(x) на границах этого интервала (рисунок 4).

.

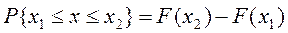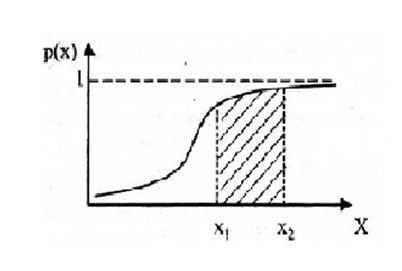
Рисунок 4 – Определение вероятности попадания отдельного значения в заданный интервал по функции распределения вероятности