Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Самостоятельного изучения
|
|
УЧЕБНОЕ ПОСОБИЕ ДЛЯ
Составитель В. М. Лазарев
Томск, 2009.
Содержание:
1. Предмет и задачи геодезии……………………………………………………4
2. Понятие о фигуре Земли………………………………………………………4
3. Учет влияния кривизны Земли на измерения………………………………..5
4. Системы координат……………………………………………………………6
5. Масштаб………………………………………………………………………..7
6. Понятие о плане и карте………………………………………………………8
7. Понятие о топографической проекции Гаусса-Крюгера…………………....9
8. Номенклатура топографических карт……………………………………….10
9. Ориентирование………………………………………………………………12
10. Формы рельефа………………………………………………………………..14
11. Задачи, решаемые на топографической карте………………………………16
12. Начальные сведения из теории погрешностей измерений………………....17
13. Принцип арифметической средины…………………………………………18
14. Средняя квадратичная погрешность одного измерения.Формула Бесселя.19
15. Принцип измерения горизонтального угла…………………………………20
16. Части геодезических приборов………………………………………………21
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
16.1. Цилиндрический уровень…………………………………………….. 21
16.2. Зрительная труба……………………………………………………….22
16.3. Угломерные круги……………………………………………………...23
17. Устройство теодолита………………………………………………………...23
18. Поверки теодолита……………………………………………………………24
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
18.1. Поверка цилиндрического уровня…………………………………….25
18.2. Поверка коллимационной ошибки……………………………………25
18.3. Поверка неравенства подставок………………………………………26
18.4. Поверка сетки нитей…………………………………………………...27
19. Измерение горизонтального угла методом полного приема……………...27
20. Влияние установки теодолита и вех на измеряемое направление………...28
21. Измерение углов наклона…………………………………………………….29
22. Измерение длин линий мерными лентами………………………………….30
23. Вешение линии………………………………………………………………..31
24. Определение недоступных расстояний……………………………………..32
25. Измерения расстояний физико-оптическими дальномерами……………...33
26. Понятие о государственной геодезической сети…………………………...34
27. Прокладка теодолитных ходов………………………………………………35
28. Решение прямой и обратной геодезических задач…………………………37
29. Камеральная обработка замкнутого теодолитного хода…………………...38
30. Сущность и методы геометрического нивелирование……………………..39
31. Классификация нивелиров. Устройство нивелира Н3……………………...41
32. Поверки нивелира Н3…………………………………………………………42
33. Работа на станции технического нивелирования…………………………...43
34. Прокладка нивелирного хода………………………………………………...44
35. Камерная обработка журнала нивелирования………………………………45
36. Построение и проектирование по профилю………………………..46
37. Понятие о съемках……………………………………………………………47
38. Тригонометрической нивелирование……………………………………....47
39. Тахеометрическая съемка…………………………………………………....48
40. Работа на станции тахеометрического нивелирования…………………... 49
41. Нивелирование поверхности……………………………………………….. 49
42. Другие виды съемок………………………………………………………… 50
43. Картограмма земляных работ………………………………………………. 51
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
43.1. Вертикальная планировка. Под горизонтальную площадку………. 51
43.2. Вертикальная планировка под наклонную площадку……………… 52
44. Основные и детальные разбивочные работы в строительстве…………… 52
45. Строительная сетка………………………………………………………….. 54
46. Элементы геодезических разбивочных работ………………………………55
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
46.1. Построение проектного угла………………………………………….55
46.2. Построение линии заданной длины…………………………………..56
46.3. Построение точки с заданной отметкой…………………………….. 56
46.4. Построение линии заданного уклона……………………………….. 57
47. Способы разбивки сооружений…………………………………………….. 57
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
47.1. Способ прямоугольных координат…………………………………...58
47.2. Способ полярных координат………………………………………….58
47.3. Способ угловых засечек……………………………………………….58
47.4. Способ линейных засечек……………………………………………..58
47.5. Способ створов…………………………………………………………58
47.6. Способ разбивки от местных предметов……………………………..59
48. Изыскания инженерных сооружений………………………………………..59
49. Предварительные изыскания………………………………………………...59
50. Окончательные изыскания…………………………………………………...60
51. Строительство подземных трубопроводов………………………………….62
52. Геодезические работы по прокладке подземных трубопроводов…………62
53. Исполнительная съемка подземных коммуникаций……………………….63
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
Тема № 1 Предмет и задачи геодезии.
Геодезия - это наука об измерениях на земной поверхности и их математической обработке с целью решения различных задач.
При этом приборы и сами измерения называются геодезическими.
Основные измерения: угловые, линейные, высотные.
В зависимости от задач и способов их решения геодезия делится на несколько самостоятельных дисциплин:
1. Высшая геодезия:
а) Определение размеров, фигуры Земли (как планеты Солнечной системы) и ее внешнего гравитационного поля;
б) Определение движения материков и отдельных частей земной коры;
в) Изучение размеров, фигуры и создания карт планет Солнечной системы.
г) Создание государственных опорных геодезических сетей.
2. Картография - создание и размножение топографических карт поверхности Земли
3. Инженерная геодезия - решение практических задач геодезии применительно к строительным специальностям, связанных с изысканием, проектированием, строительством и эксплуатацией инженерных сооружений.
А также ряд других дисциплин.
Тема № 2 Понятие о фигуре Земли.
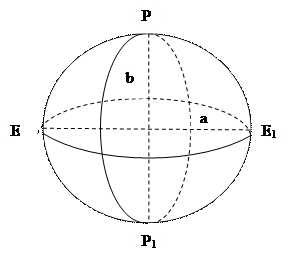Если бы Земля была неподвижным однородным телом, она имела бы форму шара. При вращении, под действием центробежной силы она окажется сплюснутой у полюсов и примет форму эллипсоида вращения, который характеризуется двумя параметрами: большой полуосью a и малой - b (или большой полуосью и коэффициентом сжатия 
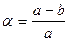). На такой поверхности направление силы тяжести и нормали к поверхности в каждой точке не совпадают. В силу неоднородности Земли, массы внутри планеты расположены неравномерно, в результате поверхность становится очень сложной.
Определение: Поверхность, совпадающая с невозмущенной поверхностью морей и океанов и мысленно продолженная под материками при условии перпендикулярности силе тяжести, называется геоидом (землеподобный).
Для математической обработки геоид неудобен. Поэтому выбирают более простую поверхность - эллипсоид вращения, соответствующих размеров и соответствующим образом расположенный (ориентированный) внутри Земли. В нашей стране используется эллипсоид, параметры которого были получены в 1940г. Ф.Н.Красовским:
а=6378245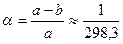 
Тема № 3 Учет влияния кривизны Земли на измерения.
Пусть АВ часть поверхности Земли принимаемая в первом приближении за сферу с центром О и радиусом R = 6371, 11 км. Дуге АВ соответствует центральный угол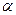 
. Заменим участок сферической поверхности плоскостью, касающейся сферы в точке А. Для учета искажений расстояния, определим разность между длиной касательной AB1 = d и дуги AB = s. Вычислим 
.
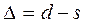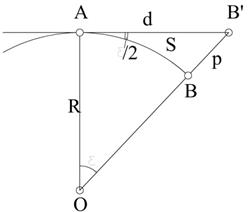Из рисунка 
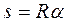, где 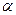- выражено в радианах. Тогда 
.
|
|
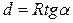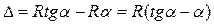
Разложим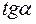 
в ряд, получим с точностью до второго члена 
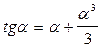, тогда подставив 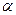, получим 
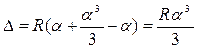, подставив 
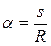получим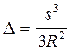 
Приняв s = 20 км, получим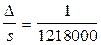 
.
Так как современные средства позволяют измерять расстояния с точностью 1/1000000 то участок размером 20х20 км можно считать горизонтальным. При решении инженерных задач за плоскость можно принимать участок 50х50 км.
Рассмотрев аналогичную задачу для учета влияния кривизны Земли на определение высот получим, что точка В переместится в точку В! . Из рисунка угол ВАВ! =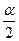 
. Так как угол мал отрезок ВВ! = p можно рассматривать как дугу радиуса s, т.е. 
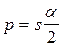, поскольку 
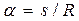, то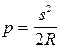 
.
Придавая s различные значения получим, что уже при расстояниях, превышающих 1 км необходимо учитывать кривизну Земли и вносить соответствующие поправки в измеренные высоты точек.
Тема№ 4 Системы координат.
В геодезии используются несколько систем координат в зависимости от поставленных задач и способов их решения:
а) Географическая
Определим систему координат следующим образом:
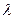- долгота - двугранный угол, образованный плоскостью
Гринвичского(нулевого) меридиана и меридиана, проходящего через точку.
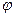- широта – угол, образованный радиус-вектором точки и плоскостью экватора.
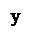
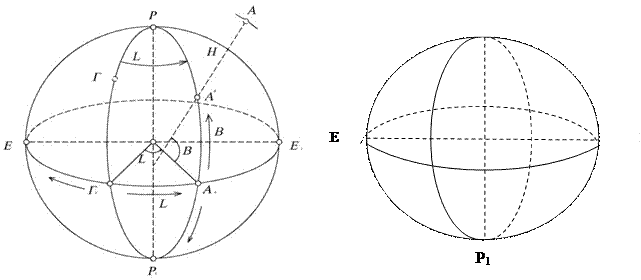
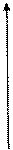Если радиус-вектор совпадает с нормалью к поверхности, то система координат – геодезическая, если с направлением силы тяжести – астрономическая. Если пренебречь сжатием и отклонением нормали от направления силы тяжести, то обобщением вышеуказанных систем координат будет географическая система координат. Третья пространственная координата: высота H на территории России отсчитывается от среднего уровня Балтийского моря.
б) Пространственная прямоугольная система координат (геоцентрическая)
Начало координат расположено в центре асс Земли. Ось Z направлена по оси вращения планеты в северном направлении. Ось Х направлена в точку пересечения гринвичского меридиана и экватора. Ось Y дополняет систему до правой. Наиболее часто эта система применяется в спутниковой (космической) геодезии при наблюдениях за искусственными спутниками Земли.
в) Плоская прямоугольная система координат (местная)
Так как на небольших участках кривизной Земли можно пренебречь, то на строительной площадке используется местная система прямоугольных декартовых координат с началом обычно в юго-западном углу площадки. Но в отличие от математики эта система координат не правая, а левая, поэтому меняется нумерация четвертей. Формулы тригонометрии остаются без изменений. Измерение высот проводится чаще всего в условной системе высот
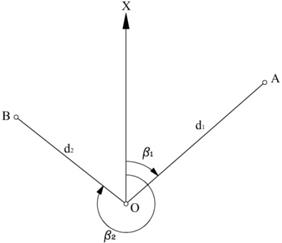г) Полярная система координат
При измерениях и построениях на строительной площадке используют полярную систему координат, которая характеризуется следующими параметрами: Полюс О, полярная ось ОХ, радиус-вектор d, полярный угол β.
Тема № 5 Масштаб.
Определение: Масштабом называется отношение длины линии d на плане или карте к длине горизонтальной проекции S той же линии на местности.
Определени е: Горизонтальной проекцией S называется ортогональна проекция линии АВ на горизонтальную плоскость.
Рассмотрим три типа масштабов:
1. Численный масштаб - правильная дробь, числитель которой единица, а знаменатель - число показывающее во сколько раз горизонтальные проекции линий местности уменьшены на плане или карте. На карте указывается разъяснение. (Например: Масштаб 1: 10000, в 1 см 100 м)
2. Линейный масштаб – графическое изображение численного масштаба. Представляет собой отрезок линии, разделенный на равные отрезки, которые называются основанием. Они нумеруются слева направо, начиная со второго. Крайнее левое основание делится на части для увеличения графической точности данного масштаба.
Определение: Длина линии на местности, соответствующая 0, 1 мм на плане или карте данного масштаба называется точностью (предельной точностью) масштаба.
3. Поперечный масштаб - расширение линейного масштаба для измерения длины с максимальной точностью 0.1-0.2 мм. Cтроится следующим образом: параллельно линии линейного масштаба проводится m линий. Верхняя линия делится на части, также как нижняя.
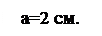
Так как чаще всего n=m=10, то имеем целое основание, АВ - десятая доля основания, СД - сотая доля основания. 
Если основание масштаба равно 2 см, то такой масштаб называетсянормальным.
Удвоенная предельная точность масштаба называется графической точностью масштаба.
При построении линий на плане или картевеличиной, равной или меньшей, чем точность масштаба можно принебречь.
Задачи, решаемые с использованием точности масштаба:
1. Определить минимальный отрезок на местности, который можно изобразить на плане или карте данного масштаба
2. Определить минимальный участок на местности, который можно изобразить в данном масштабе.
Тема № 6 Понятие о плане и карте
Поверхность сферы нельзя развернуть на плоскость без искажений. Для переноса точек с поверхности Земли на плоскость используют различные математические законы, которые называются картографическими проекциями. Любая картографическая проекция имеет искажения: либо линейные, либо угловые, либо и те и другие.
Определение Топографическим планом называется уменьшенное и подобное изображение небольших участков земной поверхности на бумаге. При этом кривизной Земли пренебрегают.
Определение Топографической картой называется уменьшенное согласно выбранной картографической проекции изображение больших участков Земной поверхности с учетом кривизны Земли.
На планах и картах изображается и ситуация и рельеф.
Ситуация - совокупность контуров и неподвижных местных предметов.
Ситуацию изображают с помощью условных топографических знаков.
Рельеф - совокупность неровностей Земной поверхности естественного происхождения.
Карты выполняются в масштабе 1: 10000, 1: 50000, 1: 100000 и мельче.
Планы выполняются в более крупных масштабах 1: 500, 1: 1000, 1: 2000, 1: 5000.
Тема № 7 Понятие о картографической проекции Гаусса - Крюгера.
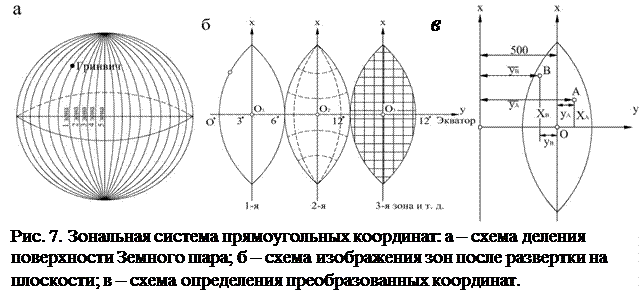
Поверхность земного шара разделим на 6о зоны, начиная от Гринвичского (нулевого) меридиана и пронумеруем их к востоку от нулевого меридиана от 0 до 60. В каждой зоне проведем центральный (осевой) меридиан.
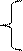Впишем земной шар в цилиндр. Повернем его так, чтобы осевой меридиан 1ой зоны касался цилиндра и перенесем все точки зоны на цилиндр согласно проекции Гаусса-Крюгера. В общем виде 
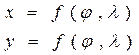т.е. каждой точке С на шаре с географическими координатами φ, λ ставится в соответствие точка С с прямоугольными координатами х, у уже на плоскости. Аналогично для зон 2, 3 и т.д. После проектирования всех зон цилиндр мысленно разрезают по образующей и разворачивают на плоскость.
В проекции Гаусса-Крюгера есть только линейные искажения. Максимума они достигают на экваторе и составляют примерно 1/800 расстояния, для территории России искажение составляет примерно 1/1100, т.е. для карт масштаба 1: 10000 и мельче такими искажениями можно пренебречь.
Для карт более крупных масштабов для уменьшения искажений используют 3о зоны.
Свойства проекции:
1. Сохраняется равенство углов на плоскости и сфере
2. Линейные искажения малы и ими пренебрегают.
3. Все меридианы и параллели можно изображать прямыми линиями
4. 
Масштаб внутри зоны можно считать постоянным.
В каждой зоне вводится система координат х и у (Зональная система координат Гаусса - Крюгера). За начало координат принимается точка пересечения осевого меридиана зоны с экватором. Ось Х направлена по осевому меридиану к северу. Ось у направлена по экватору к востоку. Для удобства использования введенной системы координат внутри каждой зоны наносится координатная сетка (линии параллельные осям координат). Чтобы исключить отрицательные значения координаты у, начало координат мысленно переносят на 500 км влево. Для сохранения однозначности определения координат точек первые цифры (одна или две) в координате у указывают номер зоны.
Тема № 8 Номенклатура топографических карт.
Определение. Номенклатурой называется система разграфки и обозначения топографических карт.
Полученные в проекции Гаусса-Крюгера шестиградусные зоны назовём колоннами и пронумеруем от 1 до 60, начиная от меридиана с долготой 180о, тогда связь между номерами колонн и зон определяется формулой n = m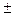 
30 (n - номер зоны, m - номер колонны)
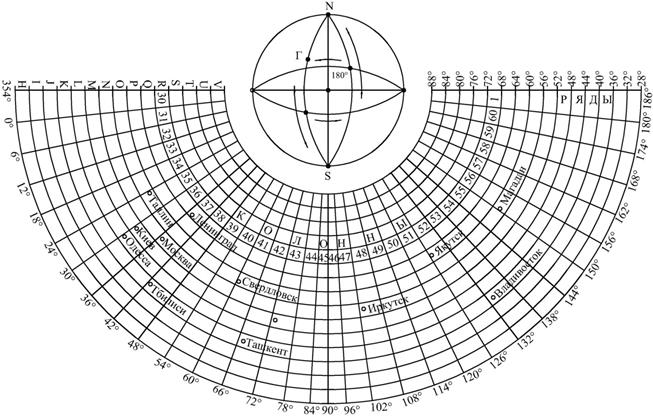
Разделим земной шар параллелями через 4о и обозначим пояса от экватора к полюсу А, В, С...V.
В результате на пересечении колонн и поясов образуется трапеция размером 4ох6о, соответствующая листу карты масштаба 1: 1000000, который является основой для топографических карт более крупных масштабов, и обозначается, например, N – 37.
Чтобы получить листы карт более крупных масштабов необходимо выполнить ряд правил:
1. Деление на листы карт более крупных масштабов проводится по параллелям и меридианам.
2. Листы более мелкого масштаба должны делиться на целое число карт более крупного масштаба.
3. В номенклатуре листов более крупного масштаба указываются номенклатуры листов более мелкого масштаба, из которых они получены. Лист карты масштаба 1: 1 000 000 делится на 144 части (12 по широте и 12 по долготе) и обозначаются цифрами от 1 до 144. Такой лист соответствует листу карты масштаба 1: 100000 и обозначается N – 37 – 144.
Лист карты масштаба 1: 100000 делится на 4 части (2 по широте и 2 по долготе) карты масштаба 1: 50000 и обозначается N – 37 – 144 – Г.
Лист карты масштаба 1: 50000 делится на 4 части (2 по широте и 2 по долготе) и обозначаются буквами а, б, в, г. Такой лист соответствует листу карты масштаба 1: 25000 и обозначается N – 37 – 144 – Г – г.
Лист карты масштаба 1: 25000 делится на 4 части (2 по широте и 2 по долготе) и обозначаются цифрами 1, 2, 3, 4. Такой лист соответствует листу карты масштаба 1: 10000 и обозначается N – 37 – 144 – Г – г – 2.
Размеры листов каждого из масштабов одинаковы.
|
Из вышеуказанного видно, что между масштабом карты и номенклатурой существует взаимно однозначное соответствие, т.е. каждому масштабу соответствует своя номенклатура, и каждой номенклатуре соответствует свой масштаб.
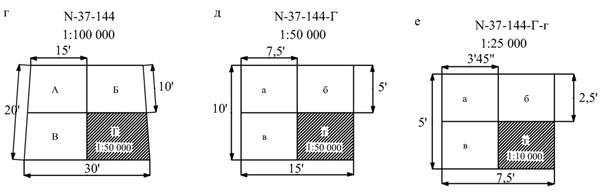
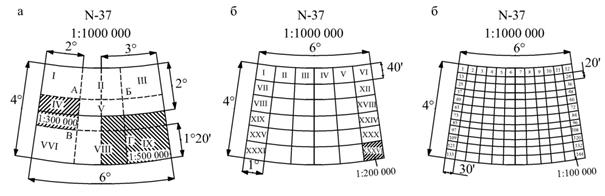
Лист карты масштаба 1: 100000 служит основой для листов плана масштаба 1: 5000 и 1: 2000. Одному листу карты масштаба 1: 100000 соответствует 256 (16 по долготе и 16 по широте) листов плана масштаба 1: 5000, которые обозначаются цифрами от 1 до 256, заключенными в скобки, т.е. N – 37 – 144-(112)
Одному листу плана масштаба 1: 5000 соответствует 9(3х3) листов плана 1: 2000, которые обозначаются русскими буквами от а до и, также заключенными в скобки, т.е. N – 37 – 144-(112-г)
При съемке участков местности менее 20 км2 допускается применение прямоугольной разграфки планшетов. В основу этой разграфки положен планшет масштаба 1: 5000 размером 40х40 см, обозначаемый арабским цифрами. Ему соответствует 4 листа масштаба 1: 2000, каждый из которых обозначается присоединением к номеру планшета масштаба 1: 5000 одной из прописных букв русского алфавита А, Б, В, Г. Листу плана масштаба 1: 2000 соответствует 4 листа масштаба 1: 1000 и обозначаемых римскими цифрами I, II, III, IV и 16 листов масштаба 1: 500 (обозначаются цифрами от 1 до 16). Такая разграфка приводит к образованию планшетов масштабов 1: 2000, 1: 1000, 1: 500 размером 50х50 см
Тема № 9 Ориентирование
Определение: Ориентировать линию местности – это значит определить ее направление относительно меридиана.
Будем различать три меридиана:
1. Истинный - дуга большого круга, соединяющая географические полюса Земли.
2. Магнитный - линия на поверхности Земли, соединяющая магнитные полюса.
3. Осевой - центральный меридиан зоны проекции Гаусса - Крюгера.
Определение Азимутом называется угол, отсчитанный от северного конца меридиана по ходу часовой стрелки до данного направления. Измеряется от 0 до 360о.
В зависимости от выбранного исходного меридиана углы называются:
1. Если истинный меридиан, то угол называется истинный азимут Аи.
2. Если магнитный меридиан, то угол называется магнитный азимут Ам.
3. Если осевой меридиан, то угол называется дирекционный угол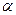
В общем случае направление меридианов не совпадает.
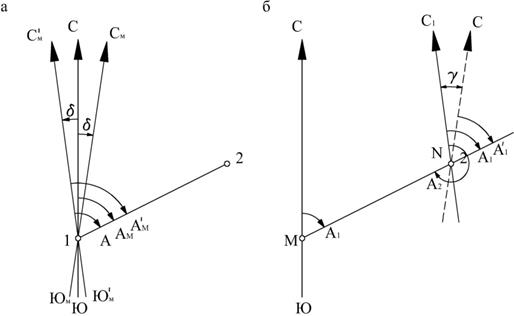
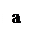
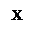
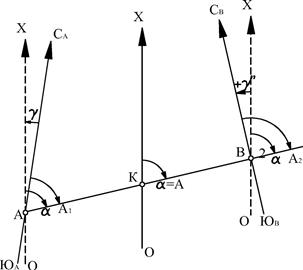
Угол между истинным меридианом и осевым называется сближением меридианов. Этот угол вычисляется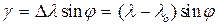 
, 
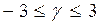. Здесь 
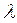- долгота точки, 
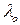- долгота осевого меридиана, 
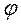- широта точки.
Угол между истинным и магнитным меридианами называется склонение магнитной стрелки. Для территории России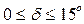 
.
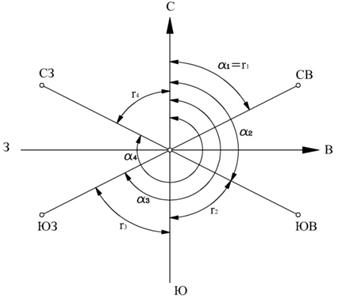Для ориентирования на карте используется дирекционный угол. На местности ориентирование осуществляется по магнитному (буссоль, компас) и истинному (гиротеодолит) азимутам. Зная значение одного из азимутов можно вычислить остальные.
Иногда используется понятие румба, чаще всего в навигации и дорожном строительстве.
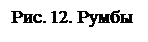Определение Румбом называется острый угол, отсчитанный от осевого меридиана. Измеряется от 0 до 
.
Тема № 10 Формы рельефа.
На планах и картах рельеф изображается с помощью горизонталей.
Определение Горизонталь - это замкнутая кривая линия, все точки которой имеют одну и туже высоту.
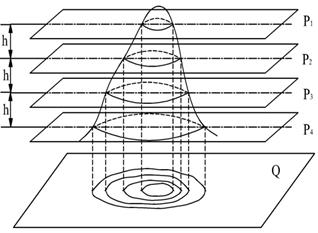h - высота сечения рельефа
a - заложение
Штрих на горизонтали, показывающий направление понижения рельефа называется бергштрихом.
Свойства горизонталей:
1. 
Все точки на горизонтали имеют одинаковые высоты.
2. 
Горизонталь - замкнутая линия.
3. 
Горизонтали не могут пересекаться.
4. Чем гуще горизонтали, тем круче скат.
Формы рельефа:
1.
|
|
2. Котловина (впадина, яма) - противоположная горе форма рельефа. Основные элементы: дно, скат, бровка.
3. Хребет - вытянутая и постепенно понижающаяся в одном направлении возвышенность. Линия, проведенная по наивысшим точкам, называется водораздел, боковые поверхности - склон.
4. Лощина - вытянутое в одном направлении углубление земной поверхности с постепенно понижающимся дном. Линия, проведенная по самым низким точкам - водослив или тальвег.
5. 
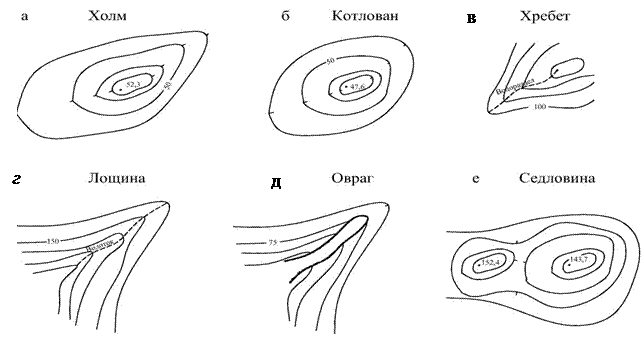Седловина - пониженный участок местности между двумя вершинами. В горах называется перевалом.
Вершина горы, дно котловины, самая низкая точка седловины, точки перегибов скатов называются характерными точками рельефа. Линии водораздела и водослива называются характерными линиями местности.
Для облегчения решения различных задач по карте горизонтали подписываются так, чтобы верх цифр был направлен в сторону повышения рельефа. Обычно подписывается либо каждая четвертая, либо каждая пятая горизонталь, в зависимости от высоты сечения рельефа.
Тема №11. Задачи, решаемые на топографической карте.
На карте решаются следующие задачи:
1. Определение географических координат точки φ, λ.
2. Определение прямоугольных координат точки Х, У.
3. Определение дирекционного угла направления α.
4. Вычисление истинного и магнитного азимутов, сближения меридианов Аи, Ам, γ.
5. Определение отметки горизонтали Н.
6. Определение отметок точек.
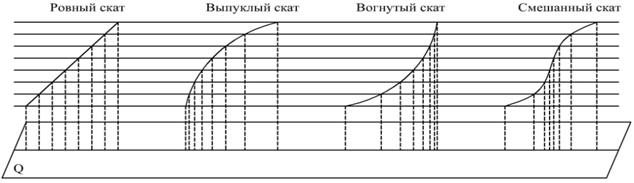
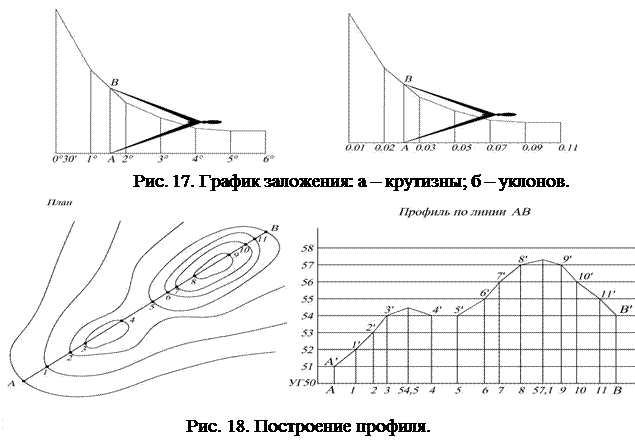
7. Определение крутизны скатов с помощью масштаба заложений.
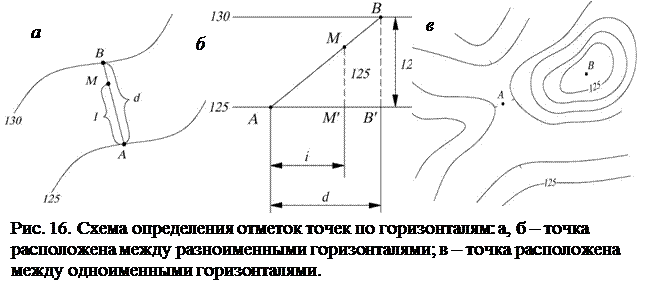
8. 
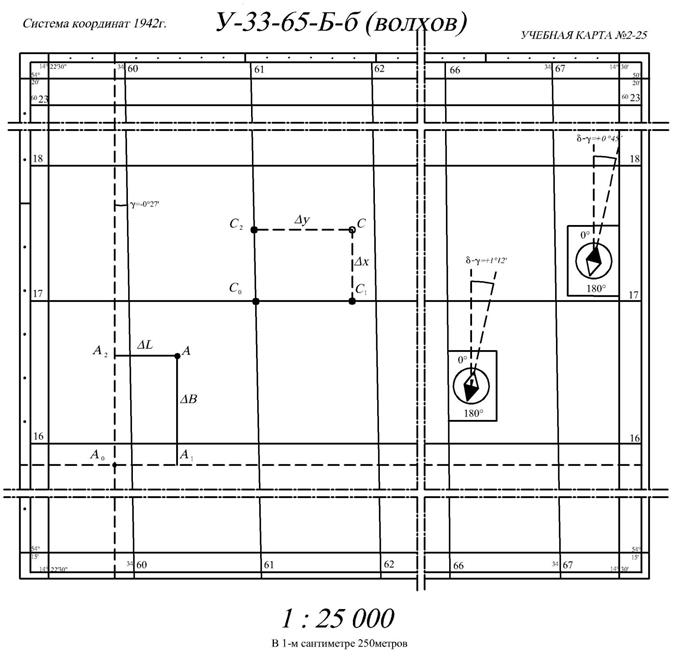Построение профиля.
|
|
Тема № 12 Начальные сведения из теории погрешностей измерений.
Измерить величину - это значить сравнить ее с однородной величиной, принятой за единицу измерений.
Любое измерение содержит ошибку (погрешность). Безошибочных измерений в природе не существует. Для выявления этих погрешностей и ослабления их влияния на результат измерения и оценки точности проводят повторные и избыточные измерения.
Если обозначить Х - истинное значение измеренной величины,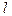 
- результат измерения, 
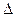- погрешность, то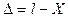 
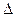- всегда неизвестна, т.к. неизвестно Х.
На процесс измерения влияет совокупность трех факторов: инструмент, внешняя среда, наблюдатель.
Ошибки делятся на три типа: а) грубые, б) систематические, в) случайные.
а) Грубые. Появляются в результате грубой ошибки наблюдателя, дефекта инструмента или неблагоприятных внешних условий. Их необходимо выявлять и отбраковывать. Методы борьбы - метод повторных и избыточных измерений.
б) Систематические. Повторяются по определенному закону. Методы борьбы - введение поправки в результат или выбор такой методики измерений, которая исключает погрешность или делает ее пренебрегаемо малой.
в) Случайные погрешности всегда присутствуют в измерениях. Учесть и компенсировать их нельзя, но в совокупности они обладают определенными свойствами, изучение которых позволяют уменьшить их влияние на конечный результат.
Свойства случайных погрешностей:
1. При данных условиях измерений одной и той же величины случайные погрешности не могут превосходить известного предела.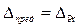 
2. Равные по абсолютной величине положительные и отрицательные случайные погрешности встречаются одинаково часто.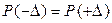 
3. Среднее арифметическое из случайных погрешностей стремится к нулю при неограниченном числе измерений. Пусть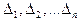 
- случайные погрешности, тогда 
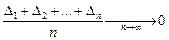обозначим 
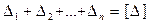, тогда 
.
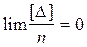4. Малые по абсолютной величине погрешности встречаются чаще, чем большие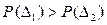 
, если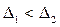 
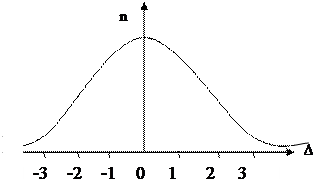Поведение случайных погрешностей подчиняется так называемому нормальному закону. График дифференциальной функции этого закона представлен на рисунке.
Тема № 13 Принцип арифметической средины.
Методов борьбы с каждой случайной величиной не существует. Однако существует способ ослабить влияние случайных погрешностей в окончательном результате. Это принцип арифметической средины.
Пусть Х - истинное значение измеряемой величины,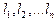 
- результаты измерений, 
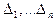- случайные погрешности, тогда 
Сложим равенства и разделим почленно на n. Тогда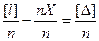 
Обозначим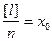 
. Очевидно, что х0 - среднее арифметическое из результатов измерений. Перейдем к пределу при 
, 
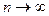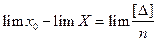, по 3 свойству случайных погрешностей 
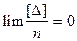. Поэтому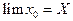 
Т.е. при неограниченном увеличении числа измерений среднее арифметическое приближается к истинному значению. Но так как на практике количество измерений, конечно, то полностью исключить влияние случайных ошибок нельзя, но вышеуказанный метод, носящий название метод арифметической средины, позволяет существенно снизить их влияние.
Результат измерений может содержать все виды ошибок. Но в дальнейшем мы будем считать, что после предварительной обработки остались только случайные погрешности.
Тема № 14 Средняя квадратическая погрешность одного измерения
Формула Бесселя.
После измерения необходимо произвести оценку точности, т.е. оценить правильность полученных результатов. Это можно сделать только тогда, когда есть повторные или избыточные измерения. Наиболее надежным и естественным критерием является дисперсия D, которая характеризует меру рассеяния результатов измерений. Т.к. на практике число измерений конечно, то приходится использовать приближенное значение, которое называется оценкой дисперсии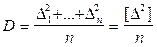 
Неудобство этой формулы заключается в том, что она имеет квадратическую размерность по сравнению с результатами измерений. Для исключения этого используют критерий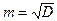 
, который называется средней квадратической погрешностью.
Свойства средней квадратической погрешности:
1. При числе измерений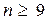 
меняется очень мало, т.е. m близко к его теоретическому аналогу 
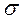, называемому стандарт, при 
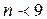оценка m ненадежна.
2. Из опыта установлено, что в ряду из 1000 измерений, только 3 случайные погрешности превышают величину 3m, которая и принимается за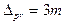 
, т.е. она и является тем пределом, о котором мы говорили в 1 свойстве случайных погрешностей.
Предельная погрешность играет важную роль при установлении допусков в различных нормативных документах.
Гаусс вывел формулу вычисления средней квадратической погрешности
, где 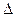- истинная погрешность.
Эта формула используется в теоретических исследованиях, но на практике применять ее нельзя, т.к. нам никогда неизвестно истинное значение измеряемой величины. Поэтому на основании формулы Гаусса, Бессель вывел формулу, которую удобно использовать на практике:
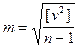, где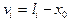 
, х0 - среднее арифметическое, vi - уклонение от арифметической средины.
Формула Бесселя используется для определения средней квадратической погрешности одной измеряемой величины. Но на практике мы часто сталкиваемся с необходимостью определить среднюю квадратическую погрешность функции измеренных величин. Для этого используется следующая формула.
Пусть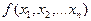 
- функция измеренных величин, тогда
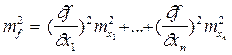, где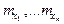 
- средние квадратические погрешности каждой измеренной величины.
Тема № 15 Принцип измерения горизонтального угла.
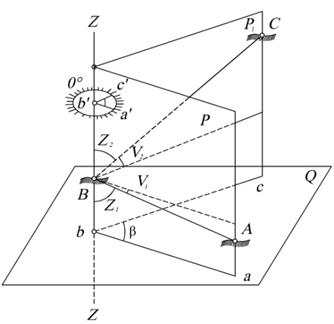
Пусть нам необходимо измерить горизонтальный угол в т. В между точками А и С. Обычно точки лежат в разных уровнях. Горизонтальным углом будет угол а1в1с1 образованный проекциями в1а1 и в1с1 на горизонтальную плоскость, проведенную в т. В.
Определение Горизонтальный угол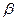 
есть мера двугранного угла между отвесными плоскостями P и P1 проходящих через стороны ВА и ВС соответственно.
Горизонтальному углу 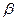будет равен любой другой угол, вершина которого находится в любой точке отвесного ребра Вb двугранного угла АВС, а стороны лежат в плоскости, параллельной Q.
Расположим горизонтально в точке b1 градуированный круг, центр которого лежит на ребре Вb.
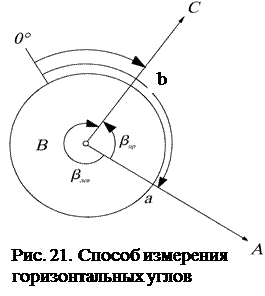Определим на этом круге начало (нулевой отсчет) и подпишем по ходу часовой стрелки. Тогда угол определится как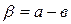 
Следовательно, для измерения горизонтального угла необходимо иметь горизонтальный градуированный круг, называемый лимбом, и подвижную (коллимационную) плоскость, вращающуюся вокруг отвесной оси ZZ1. Совмещая подвижную плоскость со сторонами двугранного угла, снимаем отсчеты по лимбу. Для точного измерения горизонтального угла необходимо выполнение следующих условий:
1. Плоскость лимба должна быть горизонтальна и неподвижна.
2. Центр лимба должен лежать на одной отвесной линии с вершиной угла.
3. Коллимационные плоскости должны быть вертикальны.
Эти условия решаются в приборе, который называется теодолит.
Тема № 16 Части геодезических приборов.
П.16.1. Цилиндрический уровень.
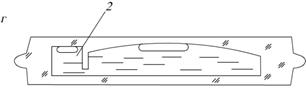
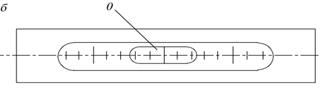
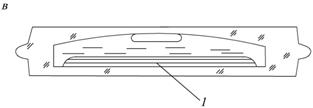
Цилиндрический уровень представляет собой стеклянную ампулу, внутренняя поверхность которой, в вертикальном разрезе, имеет вид дуги большого радиуса (от 3.5 до 200 м). При изготовлении ампулу заполняют легкоподвижной жидкостью (эфир или спирт), нагревают и запаивают. После охлаждения внутри ампулы образуется небольшое пространство, заполненное парами жидкости, которое называется пузырьком уровня.
На наружной поверхности ампулы наносятся деления через 2 мм. Средний штрих ампулы, т.е. наивысшее положение, принимается за нулевой и называется нуль-пунктом. Т.к. пары легче жидкости, то пузырек всегда стремится занять наивысшее положение. Если концы пузырька расположены симметрично относительно нуль - пункта, то говорят, что пузырек находится в нуль - пункте.
Определение Касательная uu1 к внутренней поверхности уровня в нуль- пункте называется осью цилиндрического уровня.
Центральный угол, соответствующий одному делению ампулы называется ценой деления уровня. Сейчас выпускаются уровни с ценой деления от 111 до 21. Можно доказать, что когда пузырек находится в нуль- пункте, то ось уровня горизонтальна. И наоборот.
П.16.2. Зрительная труба.
Зрительная труба предназначена для увеличения разрешающей способности глаза и точного наведения прибора на предмет (точка местности, нивелирная рейка и т.п.).
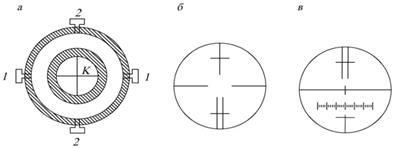
Та часть зрительной трубы, в которую смотрим называется окуляр (1), противоположная – объектив (2).
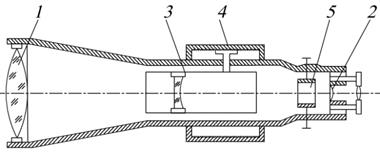
В современных приборах применяются трубы с внутренней фокусировкой.
Между окуляром и объективом ставится двояковогнутая линза, которая перемещается внутри трубы с помощью кремальеры (4). Изменение положения этой линзы меняет положение фокуса объектива, поэтому она называется фокусирующей (3). В окулярной части трубы находится стеклянная пластинка с нанесенными на нее взаимноперпендикулярными штрихами, которая называется сеткой нитей (5). Для более точного наведения используется двойной вертикальный штрих - биссектор. Точка пересечения линий называется перекрестие сетки нитей. Для наведения на резкость сетки нитей на окуляре есть специальное ребристое кольцо - окулярное колено.
Определение Визирной осью ww1 называется прямая, проходящая через оптический центр объектива, перекрестие сетки нитей и глаз наблюдателя.
П.16.3. Угломерные круги.
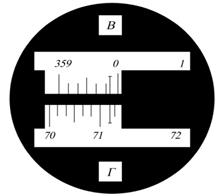Горизонтальный круг теодолита предназначен для измерения горизонтальных углов и состоит из лимба и алидады. Лимб разделен на 360 частей и каждый градус подписан. На алидаде находится приспособление, с помощью которого снимается отсчет. Вертикальный круг служит для измерения вертикальных углов (углов наклона)
Угломерные круги - это стеклянные кольца с нанесенными на них специальными приборами делениями. Расстояние между ближайшими делениями называется ценой деления.
Отсчетные приспособления делятся на три типа: верньерные, шкаловые и штриховые.
Тема № 17 Устройство теодолита
В комплект теодолита входит теодолит в футляре, штатив и две вешки, которые представляют собой двухметровые полосатые палки, диаметром 20мм, покрашенные контрастными цветами.
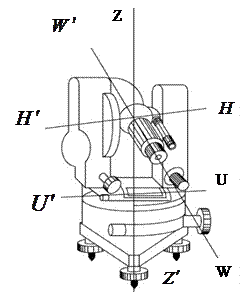Теодолит устанавливается на штатив с помощью станового винта. В нижней части находится треггер с тремя подъемными винтами для приведения оси вращения теодолита в вертикальное положение. Контролем вертикальности служит цилиндрический уровень. На треггере расположены закрепительный и наводящий (микрометренный) винты лимба для перемещения прибора в горизонтальном положении. Необходимо запомнить, что наводящие винты работают лишь тогда, когда закрепительнные винты закручены.
Под цилиндрическим уровнем находится закрепительный винт лимба для перемещения прибора в горизонтальной плоскости. Рядом с ним находится наводящий винт алидады. Сверху расположен закрепительный винт зрительной трубы для перемещения зрительной трубы в вертикальной плоскости. Над наводящим винтом алидады находится наводящий винт зрительной трубы.
Рядом с окуляром зрительной трубы находится окуляр отсчетного приспособления. С помощью специальных призм изображения горизонтального и вертикального кругов снесены в поле зрения отсчетного приспособления, а с помощью светового пучка из окошечка, находящегося сбоку, можно их увидеть.
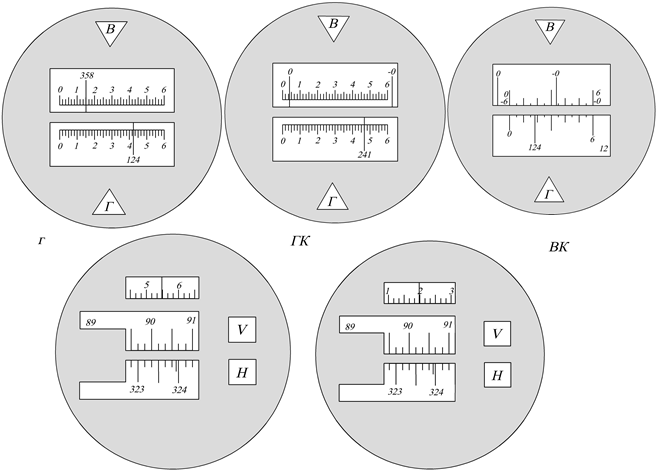Отсчеты по кругам снимаются следующим образом.
В зависимости от положения окуляра отсчетного приспособления относительно окуляра зрительной трубы различают два положения инструмента: круг лево КЛ и круг право КП.
Тема №18. Поверки теодолита.
Для обеспечения правильности работы, любой прибор должен отвечать ряду геометрических требований. В процессе эксплуатации эти требования могут нарушаться. Поэтому необходимо контролировать эти требования в процессе эксплуатации и исправлять нарушенные условия.
Определение Поверкой называется совокупность операций, направленных на осуществление контроля требуемого условия.
В теодолите такими условиями являются геометрические требования к взаимному расположению осей. Мы рассмотрим четыре оси: ось уровня UU1, ось вращения прибора ZZ1, ось вращения зрительной трубы HH1, визирную ось WW1.
П.18.1 Поверка цилиндрического уровня. UU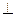1 
ZZ1
Ось цилиндрического уровня должна быть перпендикулярна ось вращения инструмента.
Эта поверка необходима для приведения оси вращения в вертикальное положение или что тоже самое, для приведения плоскости лимба в горизонтальное положение.
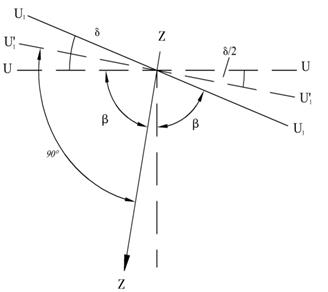Если условие выполняется, то поверка выполнена.
Если условие не выполняется, то после приведения пузырька в нуль-пункт ось UU1 займет горизонтальное положение, проведем линию, перпендикулярную оси ZZ1, которая образует с осью угол 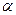. При развороте на 1800 отклонение составит 
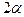, на величину 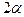сместится и пузырек уровня, что указывает на невыполнение условия. Исправление производится исправительными (юстирными) винтами на величину 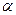. После этого поверка производится заново до тех пор пока условие не будет выполнено.
П.18.2. Поверка коллимационной ошибки.
Визирная ось должна быть перпендикулярна оси вращения зрительной трубы.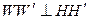 
Невыполнение этого условия влечет ошибку при снятии отсчетов по лимбу. Поверка выполняется следующим образом: на расстоянии 60-70 м выбирается точка, на нее наводится прибор и снимается отсчет при круге право и при круге лево. После этого вычисляется величина коллимационной ошибки по формуле:
Если величина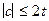 
то условие выполнено, в противном случае вычисляем истинный отсчет по формуле: 
.
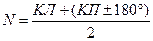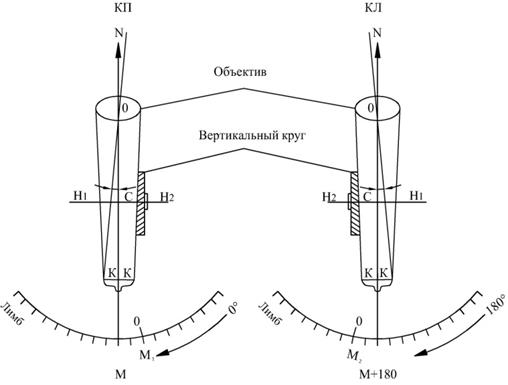
На отсчетном приспособлении устанавливаем вычисленный отсчет по горизонтальному кругу. В этом случае изображение точки наведения сместится из перекрестия сетки нитей. С помощью юстирных винтов, находящихся под кожухом окуляра зрительной трубы, перемещаем сетку нитей так, чтобы изображение вернулось в перекрестие и проводим поверку заново.
Из формулы вычисления истинного отсчета следует, что коллимационная ошибка автоматически исключается, если из двух отсчетов при КЛ и КП брать среднее.
П.18.3. Поверка неравенства подставок.
Ось вращения зрительной трубы должна быть перпендикулярна оси вращения инструмента.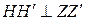 
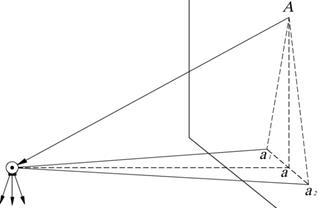Невыполнение этого условия не позволяет добиваться вертикальности коллимационных плоскостей, что в свою очередь влечет искажение отсчетов по лимбу.
Порядок проведения поверки. Выбирается высоко лежащая точка на расстоянии 15-20 м. Наводится на нее теодолит при одном из кругов и затем зрительная труба опускается до уровня горизонта, полученная в результате точка фиксируется. Затем это же проводят при другом круге. Если в результате полученные точки совпадут, то условие выполнено. В противном случае требуется исправление, которое выполняется в специальных мастерских
При невыполнении этого условия, как и в случае с коллимационной ошибкой, можно найти правильный отсчет воспользовавшись формулой для вычисления.
П.18.4. Поверка сетки нитей.
Горизонтальный штрих сетки нитей должен быть перпендикулярен к оси вращения прибора.
Порядок проведения поверки. Выбирается далеко расположенная точка. Наводим на нее теодолит так, чтобы изображение точки располагалось в крайнем левом положении на горизонтальном штрихе сетки нитей.
Затем с помощью наводящего винта алидады перемещаем изображение из крайнего левого положения в крайнее правое. Если в результате изображение точки осталось на сетке нитей, то условие выполнено. В противном случае с помощью юстирных винтов поворачиваем сетку нитей и производим поверку заново.
После окончательного исправления необходимо вновь выполнить поверку коллимационной ошибки.
Тема №19 Измерение горизонтального угла методом полного приема.
Прежде чем измерять горизонтальный угол необходимо определить точность, с которой требуется измерить угол. В зависимости от точности теодолиты делятся на три класса:
1. Высокоточные Т05, Т1 - предназначены для измерения углов в триангуляции и полигонометрии 1 и 2 классов.
2. Точные Т2, Т5 - для измерения углов в триангуляции и полигонометрии 3 и 4 классов, 1 и 2 разрядов.
3. Технические Т15, Т30, Т60 - для измерения углов в теодолитных и тахеометрических ходах, съёмочных сетях.
В условных обозначениях теодолитов цифра означает среднюю квадратическую погрешность горизонтального угла одним приемом в секундах.
Все перечисленные теодолиты имеют более современные модификации: 2Т2, 2Т5К, 2Т30 и т.д.
До начала работы необходимо выполнить ряд операций для правильного измерения:
1. Центрирование. С помощью отвеса (нитяного или оптического) устанавливают инструмент точно над точкой. В результате центрирования достигается условие, что центр лимба и вершина угла лежат на одной отвесной линии.
2. Приведение оси вращения теодолита в вертикальное положение. Производится с помощью подъемных винтов. Устанавливаем цилиндрический уровень параллельно плоскости двух подъемных винтов. Приводим пузырек в нуль-пункт и поворачиваем теодолит на 900 и вновь приводим пузырек в нуль-пункт. Если у теодолита выполнено условие поверки уровня, то этого достаточно для дальнейшей работы.
Проведение вышеперечисленных операций называется приведением инструмента в рабочее положение.
Обязательным условием правильного измерения угла является неподвижность лимба, причем измерение можно начинать с любого положения теодолита. Угол измеряют дважды при КЛ и КП в следующем порядке. Наводят перекрестие сетки нитей на точку, лежащую правее и снимают отсчет, затем, не меняя круга, наводят на левую точку и вновь снимают отсчет. От отсчета по правой точку вычитают отсчет по левой. Разность отсчетов даст горизонтальный угол между этими точками. Затем тоже самое проводят при другом круге.
Если расхождение между двумя значениями не превышает двух точностей инструмента, то угол измерен правильно и в качестве результата берется среднее из двух углов. Если же расхождение больше, то угол необходимо перемерить.
Предложенная методика обладает следующими достоинствами:
1. Позволяет произвести контроль и отбраковку измерений в случае расхождения углов в полуприемах более чем на две точности теодолита.
2. Позволяет автоматически и полностью исключить коллимационную ошибку.
3. Позволяет автоматически и полностью исключить влияние неперпендикулярность оси вращения теодолита и оси вращения зрительной трубы.
4. Позволяет автоматически и полностью исключить влияние эксцентриситета (несовпадения оси вращения теодолита и центра лимба).
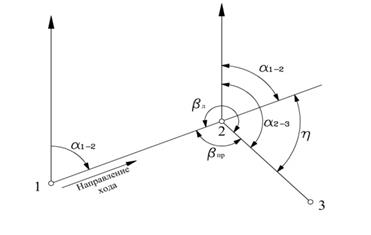
Тема № 20 Влияние установки теодолита и вех на измеряемое направление.
Пусть А точка стояния, а В - точка наведения. (Рис. 31)
Из-за ошибки центрирования центр лимба будет над точкой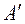 
, следовательно линией визирования будет линия 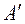В. Это приведет к погрешности в отсчетах. Обозначим 
- величина линейного смещения.
Из треугольника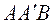 
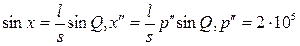. Из анализа видно, что xmin при Q = 00 и Q = 1800, т.е. когда т.А1 находится на линии АВ впереди или сзади т. А и максимально при Q = 900 и Q = 2700.
Аналогичная ситуация при неправильной установке вехи в т. В. Из треугольника АВВ1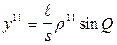 
т.е. ymin при Q = 00 и Q = 1800, и 
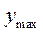при Q = 900 и Q =2700
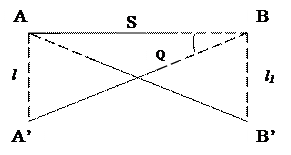
Величины х и у называются погрешностями центрирования и редукции и пропорциональны сдвигам и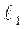 
и обратно пропорциональны расстоянию между точками. Из анализа у можно сделать вывод, что если нельзя поставить веху в т. В, то её надо ставить или перед или за т. В.
Тема № 21 Измерение углов наклона.
Определение Углом наклона называется угол, образованный визирной осью с плоскостью горизонта. Углы наклона могут быть положительными и отрицательными.
Измеряются с помощью вертикального круга.
Для измерения угла наклона необходимо фиксировать горизонтальную плоскость, что достигается с помощью уровня при алидаде горизонтального круга. В некоторых приборах имеется специальный уровень при вертикальном круге или компенсатор.
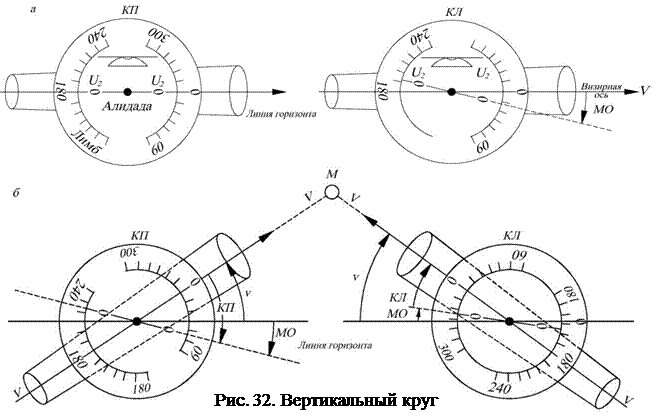
В теодолите 2Т30 вертикальный круг наглухо закреплен со зрительной трубой и вращается вместе с ней. В устройстве при приведении в рабочее положение при горизонтальном положении визирной оси должны совпадать нулевые штрихи вертикального круга и отсчетного микроскопа. Чаще всего на практике это не так.
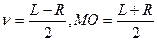
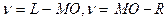
Эти формулы для теодолита 2Т30. Для различных типов теодолитов формулы могут немного отличаться. В принципе можно добиться того, что место нуля будет равняться нулю.
Определение: Местом нуля вертикального круга называется отсчет по вертикальному кругу при горизонтальном положении визирной оси трубы.
Тема № 22 Измерение длин линий мерными лентами.
Расстояние между точками местности можно измерить непосредственно и косвенно. Непосредственные измерения проводятся с помощью стальных мерных лент и рулеток. При косвенных - измеряются некоторые другие величины, а расстояние вычисляется.
Стальная лента представляет собой металлическую полосу, обычно изготовленную из стали или инвара, длиной 20 или 24 м, шириной 15-20 мм и толщиной 0.3-0.4 мм. Она разделена н
|