
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Законы распределения дискретных случайных величин.
|
|
Определение. Законом распределения случайной величины называется всякое описание (аналитическое, графическое, табличное), устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Закон распределения случайной величины определяется её типом.
Рассмотрим дискретную случайную величину 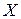 , которая принимает в результате опыта одно из единственно возможных значений
, которая принимает в результате опыта одно из единственно возможных значений 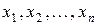 , то есть произойдет одно из полной группы несовместных событий:
, то есть произойдет одно из полной группы несовместных событий:
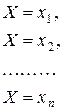 (1)
(1)
Обозначим через 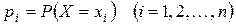 вероятность случайного события, состоящего в том, что случайная величина Х принимает значение
вероятность случайного события, состоящего в том, что случайная величина Х принимает значение 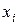 . Так как события (1) образуют полную группу событий, то сумма вероятностей всех возможных значений случайной величины Х равна единице, поэтому
. Так как события (1) образуют полную группу событий, то сумма вероятностей всех возможных значений случайной величины Х равна единице, поэтому
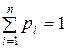 (2)
(2)
Определение. Условие (2) называется условием нормировки.
Определение. Законом распределения дискретной случайной величины называется соответствие между возможными значениями случайной величины и соответствующими вероятностями.
Простейшей формой задания закона распределения дискретной случайной величины является таблица, в первой строке которой находятся все возможные значения случайной величины, а во второй – соответствующие им вероятности:
| Х | х 1 | х 2 | … | хn |
| р | р 1 | р 2 | … | рn |
Определение. Табличное представление закона распределения дискретной случайной величины называется рядом распределения.
Для наглядности прибегают к графическому изображению ряда распределения: по оси абсцисс откладывают возможные значения случайной величины, а по оси ординат – соответствующие вероятности. Полученные точки соединяют отрезками прямых. Такая фигура называется многоугольником распределения.
Многоугольник распределения, так же, как и ряд распределения, полностью характеризует случайную величину. Однако следует помнить, что соединение точек делается только в целях наглядности, так как в промежутках между 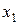 и
и 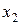 ,
, 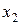 и
и 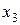 и т.д. случайная величина Х не имеет значений, а потому вероятности её появления в этих промежутках равны нулю (рис.1):
и т.д. случайная величина Х не имеет значений, а потому вероятности её появления в этих промежутках равны нулю (рис.1):
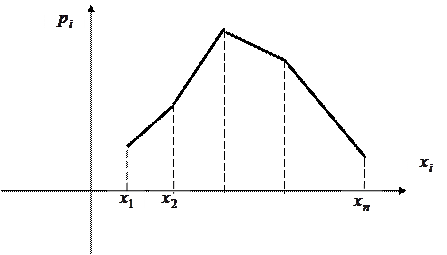
Рис.1.
Замечание. Сумма ординат вершин многоугольника распределения, представляющая собой сумму вероятностей всех возможных значений случайной величины, всегда равна единице.
Пример. Стрелок производит три выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0, 6. Построить ряд распределения и многоугольник распределения числа попаданий в цель при трех независимых выстрелах.
Решение. Возможными значениями случайной величины Х (числа попаданий) являются:
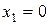 ,
, 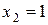 ,
, 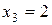 ,
, 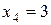 .
.
Вероятности этих значений находим по формуле Бернулли:
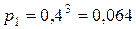 ,
, 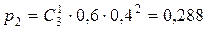 ,
,
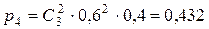 ,
, 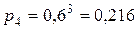 .
.
Ряд распределения величины Х имеет вид:
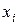
| ||||
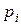
| 0, 064 | 0, 288 | 0, 432 | 0, 216 |
Многоугольник распределения изображен на рис.2.
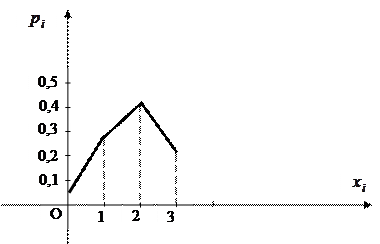 |
Рис.2.
Ряд распределения является исчерпывающей характеристикой дискретной случайной величины, однако для непрерывной случайной величины его построить нельзя. Действительно, множество возможных значений непрерывной случайной величины сплошь заполняют некоторый промежуток, и перечислить их в таблице нельзя. Для непрерывной случайной величины не существует ряда распределения в том смысле, в каком он существует для дискретной величины.
Общей формой закона распределения случайной величины Х является функция распределения. Функция распределения является универсальной характеристикой, которая существует как для непрерывных случайных величин, так и для дискретных, и полностью характеризует случайную величину с вероятностной точки зрения.
Определение. Функцией распределения (интегральным законом распределения) случайной величины Х называется функция аргумента х, задающая вероятность выполнения неравенства 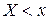 , то есть:
, то есть:
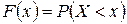 (3)
(3)
Для дискретной случайной величины Х, которая может принимать значения 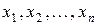 , функция распределения имеет вид:
, функция распределения имеет вид:
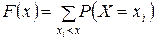 (4)
(4)
На практике функция распределения непрерывной случайной величины представляет собой непрерывную функцию, так как по мере увеличения числа возможных значений случайной величины и уменьшения интервалов между ними число скачков становится больше, а сами скачки меньше, ступенчатая кривая становится более плавной; случайная величина постепенно приближается к непрерывной величине, а её функция распределения – к непрерывной функции.
Замечание. Можно привести примеры смешанных случайных величин, для которых функция распределения в отдельных точках терпит разрыв.
Со свойствами функции распределения мы познакомимся с вами на следующей лекции.
3. Биномиальное распределение.
Среди законов распределения для дискретных случайных величин наиболее распространенным является биномиальное распределение, которое имеет место в следующих случаях.
Пусть случайная величина Х - это число появлений события А при n независимых испытаниях, в каждом из которых вероятность появления события А постоянна и равна 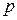 (вероятность не появления
(вероятность не появления 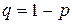 ). Возможными значениями случайной величины Х являются:
). Возможными значениями случайной величины Х являются:
 .
.
Вероятности этих возможных значений вычисляются по формуле Бернулли:
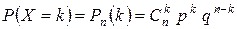 (5)
(5)
Определение. Распределение дискретной случайной величины, ряд распределения которой задается формулой (5), называется биномиальным.
Пример. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0, 1. Составить закон распределения числа отказавших элементов в одном опыте.
Решение. Обозначим через Х дискретнуюслучайную величину – число отказавших элементов в одном опыте. Возможными значениями Х являются:
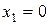 (ни один из элементов устройства не отказал),
(ни один из элементов устройства не отказал), 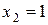 (отказал один элемент),
(отказал один элемент), 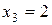 (отказали два элемента),
(отказали два элемента), 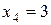 (отказали три элемента).
(отказали три элемента).
Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что 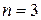 ,
, 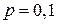 ,
, 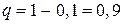 , получим:
, получим:
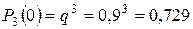 ,
, 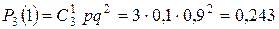 ,
,
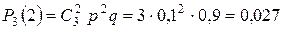 ,
, 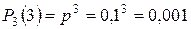 .
.
Следует проверить, что условие нормировки при этом выполняется, то есть:
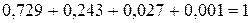 .
.
Биномиальный закон распределения имеет вид:
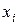
| ||||
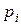
| 0, 729 | 0, 243 | 0, 027 | 0, 001 |