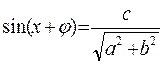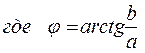Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Шпаргалки по математике.
|
|
Признаки делимости.
На 2: Если последняя цифра числа делится на 2, то число делится на 2.
На 5: Если последняя цифра числа 0 или 5, то число делится на 5.
На 10: Если последняя цифра числа 0, то число делится на 10.
На 3: Если сумма цифр числа делится на 3, то число делится на 3.
На 9: Если сумма цифр числа делится на 9, то число делится на 9.
На 4: Если последние две цифры составляют число, кратное 4 (или два нуля), то число делится на 4.
Примеры. 23.3 12 
4, 7.3 08 4, 275.6 00 4.
На 6: Если число кратно 3 и четное, то оно делится на 6.
Примеры. 714 6, 2.526 6.
На 15: Если число кратно 3 и 5, то оно делится на 15.
Примеры. 8.715 15, 2.520 15.
На 8: Если последние три цифры составляют число, кратное 8 (или три нуля), то число делится на 8.
Примеры. 7 848 8, 92 024 8, 3 008 8, 3 640 8, 75 000 8.
На 25: Если последние две цифры составляют число, кратное 25 (или два нуля), то число делится на 25.
Примеры. 3 25 25, 7.3 50 25, 275.6 00 25.
На 11: Если сумма цифр числа, занимаемых нечетные места и сумма цифр,
занимаемых четные места, равны или отличаются на число, кратное 11, то число делится на 11.
Примеры. 746.526 (4+5+6=15, 7+6+2=15), 746.526 11
281.446 (8+4+6=18, 2+1+4= 7, 18− 7=11 11), 281.446 11
28.193.209 (8+9+2+9=28, 2+1+3+0=6, 28− 6=22 11), 28.193.209 11
Формулы сокращенного умножения
| Формула | Словесная формулировка | |
| 1. | (a + b)2 = a2 + 2ab + b2 | Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа и второго и плюс квадрат второго числа. |
| 2. | (a – b)2 = a2 – 2ab + b2 | Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого числа и второго и плюс квадрат второго числа. |
| 3. | (а + b + с)2 = = а2 + b2 + c2 + 2ab + 2ac + 2bc | Квадрат суммы трёх чисел равен сумме квадратов этих чисел плюс всевозможные удвоенные произведения. |
| 4. | a2 – b2 = (a – b)(a + b) | Разность квадратов двух чисел равна произведению суммы этих чисел и их разности. |
| 5. | (a + b)3 = a3 + 3a2b +3ab2 + b3 | Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого и второго числа плюс утроенное произведение первого числа на квадрат второго и плюс куб второго числа. |
| 6. | (a – b)3 = a3 – 3a2b +3ab2 – b3 | Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого и второго числа плюс утроенное произведение первого числа на квадрат второго и минус куб второго числа. |
| 7. | a3 + b3 = (a + b)(a2 – ab + b2) | Сумма кубов двух чисел равна произведению суммы этих чисел на неполный квадрат и их разности. |
| 8. | a3 – b3 = (a – b)(a2 + ab + b2) | Разность кубов двух чисел равна произведению разности этих чисел на неполный квадрат их суммы. |
Тригонометрические формулы.
Формулы зависимости между синусом, косинусом и тангенсом одного и того же угла.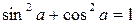 
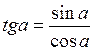
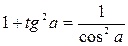
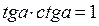
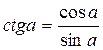
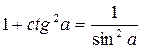
Формулы двойного угла.
; 
; 
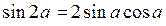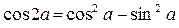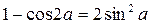
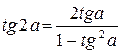
Формулы сложения.
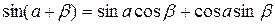
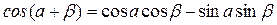
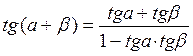
Формулы половинного угла.
; 
;
; 
;
;
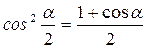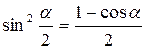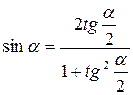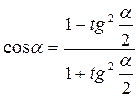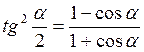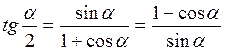
Сумма и разность синусов.
Сумма и разность косинусов.
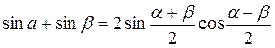
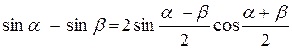
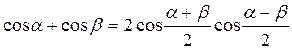
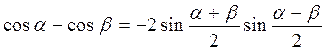
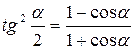
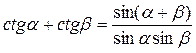
Формулы произведения.
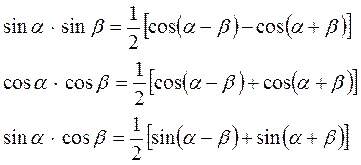
Тригонометрические уравнения
cos x = a; где a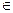 
[–1; 1]
x =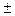 
arcos a + 2π k, k 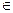Z
arcos(–a) = π – arcos a
Частные случаи:
cos x = 0;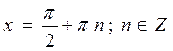 
cos x = 1;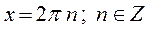 
cos x = –1;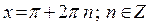 
cos(arcos a) = a; a 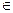[–1; 1]
arcos(cos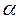 
) = ; 
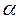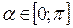
sin x = a; где a 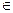[–1; 1]
x = (–1)karcsin a + π k, k 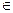Z
arcsin(–a) = –arcsin a
Частные случаи:
sin x = 0;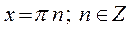 
sin x = 1;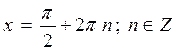 
sin x = –1; 
sin(arcsin a) = a; a [–1; 1]
arcsin(sin ) = ; 
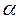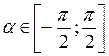
tg x = a
x = arctg a + π k; k 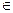Z
arctg(–a) = –arctg a
tg(arctg a) = a; a 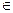Z
arctg(tg ) = ;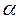 
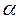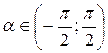
Метод дополнительного угла.
a sinx + b cosx = c
эквивалентно уравнению
