измерительного моста (одинарных)

Эту задачу рассмотрим в следующей постановке. Исследуемая ЦИП имеет вид представленный на рис.1.8 (одинарный мост постоянного тока). Активное плечо R₁ ИМ представлено на рис. в виде постоянного резистора R₁₀ и его приращения D R₁, т.е. .

Целью исследования этой ЦИП является определение рекомендаций по значению величины e_R и соотношению плеч моста. Для удобства анализа введем обозначения

,

,

где К – коэффициент симметрии ИМ.

Условие равновесия для моста постоянного тока имеет вид

R₁R₃ = R₂ R₄,

а входное(относительно генераторной диагонали) и выходное (отно-сительно измерительной диагонали) сопротивления измерительного моста соответственно определяются выражениями

R_вх = R₁R₂/ (R₁ + R₂) + R₃R₄/ (R₃ + R₄)

R_вых =(R₁ + R₂) (R₃ + R₄)/ (R₁ + R₂ + R₃ + R₄)

В теории ИМ постоянного тока получено выражение для функции преобразования в виде

(1.3)

Рис. 1.8. Схема измерительного моста в задаче

параметрического синтеза

Это выражение (3) для функции преобразования ИМ является обобщающим и для ЦИП реализованных на основе делителя напряжения. В некоторых случаях функция преобразования записывается в виде

. (1.4)

Важными параметрами ИМ постоянного тока является его входное и выходное сопротивление, которое определяются в соответствии с выражениями:

(1.5)

Чувствительность ИМ постоянного тока определяется зависимостью

. (1.6)

Графически выражение (6) представлено на рис.1.9 из которого следует, что оптимальная чувствительность достигается в случае

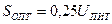при K =1 (1.7)

Анализ чувствительности ИМ постоянного тока проведем с целью оценки линейности функции преобразования. Исследование показывает, что функция преобразования такого ИМ линейна при условии при K =1.

Самая высокая линейность функции преобразования наблюдается в случае когда активными, т.е. зависимыми от измеряемой величины являются два противоположных плеча моста. Линейность функции преобразования минимальна при активных смежных (относительно измерительной диагонали) плечах моста.

Увеличения числа активных плеч моста приводит к повышению выходного напряжения ИМ, но не изменяет его чувствительность, как это следует из зависимости:

(1.8)

Такое включение характерно для тензометрических мостов. С увеличением питающего напряжения чувствительность ИМ возрастает (при К=const), как это следует из зависимости (7).

Изменение коэффициента симметрии ИМ К в небольших пределах незначительно влияет на чувствительность. Так, например, при К Î [0, 6…1, 5] чувствительность мостовой схемы уменьшается на 4% от ее значении при К= 1. Резкое изменение чувствительности наблюдается при значениях K> 2, 0и K < 0, 4.

При анализе линейности ИМ оценку линейности функции преобразования проведем на основе зависимости

(1.9)

Проведем анализ различных вариантов включения рабочих резисторов в плечи измерительного моста, т.е. варианты мостовых схем, в которых активными являются два плеча, причем различие состоит в том.

Вариант первый: в мостовой схеме (рис.1.6) одно активное плечо

e_R= e₁ (или e_R= e₂).

Вариант второй в мостовой схеме (рис.1.7) два активных плеча

Графики, представляющие зависимость (1.9), для рассматриваемых вариантов показаны соответственно на рис. 1.10 и рис.1.11

Из выражения (1.4) следует, что эта зависимость в общем случае нелинейна, поэтому графики на указанных отражают указанный вывод. Для первичных преобразователей неэлектрических величин, построенных на основе тензорезисторов для ИМ обычно принимают коэффициент симметрии K = 1, 0, а величина относительного изменения сопротивления практически не превышает e_R= 0, 1. При этом условии величина нелинейности функции преобразования рассматриваемой ЦИП с одним активным плечом составляет около 5%.

При этих же условиях и двух активных плечах (например, первое и третье в случае их уменьшения) нелинейность функции преобразования не превышает 3%, (график D, E, F) если же активными являются второе и четвертое плечо и их значения увеличиваются, то нелинейность функции преобразования данной ЦИП может достигать приблизительно 6%.

Из сравнения нелинейности функции преобразования ЦИП с одним или двумя активными плечами видно, что при работе ИМ с двумя рабочими активными плечами при любом из рассмотренных сочетаний параметров ИМ, нелинейность функции преобразования меньше, чем при работе с одним активным плечом. Для вариантов ИМ, в которых активными являются более двух плеч, нелинейность функции преобразования, как показано в работе [], зависимостью

g=(U _ВЫХ– U _{ВЫХ.ЛИН.})/ U _{ВЫХ.ЛИН.} (1.11)

Из выражения (1.10) следует, как показано в работе [], что

g= f (K, e₁, e₂, e₃, e₄) (1.12)

Анализ зависимости 1.12 позволяет провести исследование ИМ и получить условие линейности функции преобразования. Одним из таких условий является равенство между собой относительных сопротивлений e₁, e₂, e₃, e₄ плеч ИМ при коэффициенте симметрии К =1.

Если в ИМ рабочим является только одно плечо, то величина нелинейности определяется выражениями

(1.13)

(1.14)

На основе зависимостей 1.12 и 1.13 построены графики рис.1.12, 1.13.

Рис. 1.10 Рис.1.11

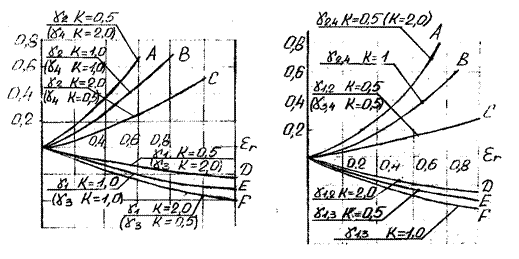
Рис. 1.12 Рис.1.13

На основе анализа этих графиков можно сформулировать следующие рекомендации по синтезу ИМ на постоянном токе.

Для ИМ с одним активным плечом необходимо выбирать такой его режим работы, чтобы в процессе измерения сопротивление этого плеча увеличивалось по мере роста измеряемой величины, а коэффициент симметрии К < 1, причем активным является первое плечо (рис.1.6). Если активным является четвертое плечо, то К ³ 1.

Необходимо выбирать ИМ с коэффициентом К =1 и двумя (смежными относительно измерительной диагонали) активными плечами или четырьмя активными плечами относительное изменение сопротивления e_R которых одинаково.

При невозможности обеспечения относительных изменений сопротивлений плеч моста одинакового знака необходимо так проектировать измерительный мост, чтобы сопротивление активных плеч в процессе работы уменьшались, а коэффициент симметрии был равен 1.

Рассмотренный анализ нелинейности функции преобразования ИМ базировался на зависимости 1.11, в которой линейная характеристика определялась, как касательная к фактической характеристике функции преобразования в начале координат. Такая оценка нелинейности не всегда удобна, однако применение другого метода оценки нелинейности функции преобразования не изменяет соотношений между ее нелинейностями для различных вариантов выполнения ИМ и режима работы его плеч. Поэтому приведенные выше рекомендации по проектированию ИМ по постоянному току остаются справедливыми.