Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Если это условие выполняется, прямые или параллельны или пересекаются.
|
|
Уравнение вида Ах+Ву+С=0(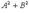
> 0). при произвольных коэффициентах А, В, С (А и В одновременно не равны нулю) определяют некоторую прямую в прямоугольной системе координат. Данное уравнение называется общим уравнением прямой.
Уравнение прямой в отрезках
где a, b - величины отрезков, отсекаемых прямой на осях координат.
Уравнение прямой по точке и вектору нормали. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой, заданной уравнением Ах + Ву + С = 0.
Уравнение прямой, проходящей через две точки. Пусть в пространстве заданы две точки M 1 (x 1, y 1, z 1) и M2 (x 2, y 2, z 2), тогда уравнение прямой, проходящей через эти точки: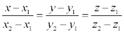 
Уравнение прямой по точке и угловому коэффициенту. Если общее уравнение прямой Ах + Ву + С = 0 привести к виду: 
и обозначить 
, то полученное уравнение называется уравнением прямой с угловым коэффициентом k
Уравнение прямой по точке и направляющему вектору Каждый ненулевой вектор 
(α 1, α 2), компоненты которого удовлетворяют условию А α 1 + В α 2 = 0 называется направляющим вектором прямой Ах + Ву + С = 0.
Нормальное уравнение прямой Если обе части уравнения Ах + Ву + С = 0 разделить на число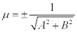 
, которое называется нормирующем множителем, то получим xcosφ + ysinφ - p = 0 – нормальное уравнение прямой. Знак ± нормирующего множителя надо выбирать так, чтобы μ * С < 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.
Уравнение прямой с угловым коэффициентом имеет вид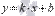 
, где k - угловой коэффициент прямой, b – некоторое действительное число. Уравнением прямой с угловым коэффициентом можно задать любую прямую, не параллельную оси Oy