
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Исследование зависимости сопротивления металлов от температуры
|
|
Приборы и принадлежности: печь (плитка), металлический проводник, термометр, термопара.
Цель работы: изучить температурную зависимость сопротивления металлов, полупроводникового термистора; определить термический коэффициент сопротивления меди и энергию активации в полупроводнике.
Теоретическое введение
Электрическое сопротивление проводников зависит от температуры. У металлов оно возрастает при нагревании, у электролитов – при охлаждении. Зависимость сопротивления металлов от температуры можно выразить соотношением:
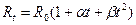 (1)
(1)
где R0 и Rt – значения сопротивления соответственно при 00 C и при температуре t; a и b – константы, характерные для данного металла. Приближенно выражение (1) можно записать:
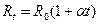 (2)
(2)
Если в исследованном диапазоне температур коэффициент a – величина постоянная, то формула (2) представляет собой уравнение прямой в координатах Rt и t (рис.1).
По тангенсу угла ее наклона к оси абсцисс можно определить коэффициент a, называемый термическим коэффициентом сопротивления.
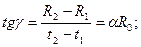
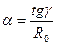 (3)
(3)
Опыт показывает (и это хорошо согласуется с теорией), что проводимость полупроводника изменяется с температурой по экспоненциальному закону:
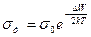 (4)
(4)
где sт – удельная электропроводность при данной температуре;
s0 – некоторая постоянная для данного полупроводника;
DW – энергия активации, равная работе переброса электронов в зону проводимости (или на акцепторный уровень);
k – постоянная Больцмана.
R 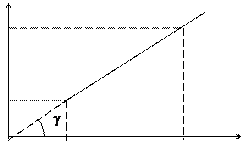
R2
R1
R0
0 t1 t2 t
Рисунок 1
С повышением температуры полупроводника увеличивается число валентных электронов, переброшенных в зону проводимости (или на акцепторные уровни). Этим и объясняется возрастание электропроводности полупроводников с температурой. Для полупроводника, имеющего форму цилиндра или призмы, величина сопротивления при данной температуре записывается в виде:
 (5)
(5)
где rт – удельное сопротивление, 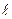 – расстояние между электродами, S – площадь поперечного сечения.
– расстояние между электродами, S – площадь поперечного сечения.
Поскольку 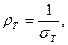 то
то  или, учитывая (4)
или, учитывая (4)
 (6)
(6)
Так как  – величина, постоянная для данного образца, то выражение (5) можно записать в виде:
– величина, постоянная для данного образца, то выражение (5) можно записать в виде:
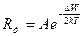 (7)
(7)
Логарифмируя (7), получим:
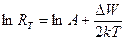 (8)
(8)
Эта формула представляет собой уравнение прямой в координатах 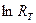 и
и 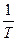 (рис.2).
(рис.2).
По тангенсу угла ее наклона к оси абсцисс можно найти 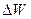 :
:
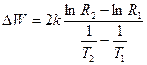 (9)
(9)
Однако в некоторых случаях линейная зависимость 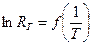 при достижении определенной температуры нарушается, что свидетельствует об изменении характера проводимости полупроводника.
при достижении определенной температуры нарушается, что свидетельствует об изменении характера проводимости полупроводника.
Электропроводность электролитов, как известно, может быть выражена формулой:
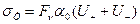
где F – число Фарадея, n – эквивалентная концентрация, a0 – степень диссоциации, U+ и U- – подвижности положительных и отрицательных ионов.
 ln RT
ln RT
ln R2
ln R1
) a
0 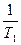
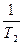
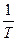
Рисунок 2
Так как степень диссоциации a 0 зависит от концентрации раствора, причем эта зависимость не является монотонной, то и электропроводность является функцией концентрации. Зависимость s = f(n) имеет сложный характер.
При постоянной концентрации степень диссоциации и подвижности ионов возрастает с увеличением температуры. Следовательно, электропроводность электролитов увеличивается с температурой, а сопротивление уменьшается.