
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Замечания.
|
|
1) Признак основан на сравнении рядов с несобственными интегралами.
2) Функцию 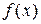 , принимающую в точках
, принимающую в точках 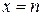 значения
значения 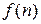 , чаще всего удается построить с помощью замены натурального
, чаще всего удается построить с помощью замены натурального 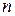 в выражении
в выражении 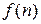 , чаще на непрерывно изменяющийся аргумент
, чаще на непрерывно изменяющийся аргумент  . Так, например, если
. Так, например, если 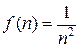 , то
, то  ; если
; если 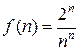 , то
, то  . Однако, не всегда таким путем можно получить функцию
. Однако, не всегда таким путем можно получить функцию 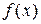 . Если, например
. Если, например 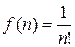 , то в этом случае нельзя заменить
, то в этом случае нельзя заменить 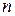 на
на  , так как символ
, так как символ 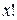 при нецельных
при нецельных  лишен смысла. Это не означает, что не существует функции
лишен смысла. Это не означает, что не существует функции 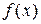 , принимающей в точках
, принимающей в точках 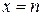 значения
значения 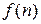 . Напротив, она всегда существует, но ее аналитическое выражение не всегда просто найти.
. Напротив, она всегда существует, но ее аналитическое выражение не всегда просто найти.
3) Достоинство интегрального признака Коши состоит в том, что он четко проводит различие между все более медленно сходящимися рядами, даже если члены одного из них лишь незначительно отличаются от членов другого, что иллюстрируется приведенным ниже примером 17.
4) Интегральный признак Коши применим к рядам, в которых положительные члены монотонно убывают с увеличением их номера. Но даже и для таких функций может оказаться, что путь непосредственного вычисления интеграла при применении интегрального признака сходимости не всегда приемлем. Например, для ряда 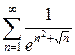 требуется вычислить интеграл
требуется вычислить интеграл  , что затруднительно. К данному ряду очевидно применение первого признака сравнения: при
, что затруднительно. К данному ряду очевидно применение первого признака сравнения: при  мы имеем
мы имеем 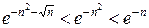 , а ряд
, а ряд 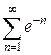 сходится как геометрическая прогрессия со знаменателем
сходится как геометрическая прогрессия со знаменателем  .
.
Пример 17. Исследовать на сходимость ряд 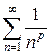 (
(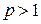 ).
).
Рассмотрим функцию 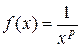 . Эта функция на промежутке
. Эта функция на промежутке  непрерывна, неотрицательна, монотонно убывает. Кроме того, для любого натурального
непрерывна, неотрицательна, монотонно убывает. Кроме того, для любого натурального 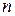
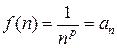 .
.
Следовательно, несобственный интеграл 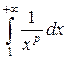 и ряд
и ряд 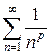 ведут себя одинаково относительно сходимости. Рассмотрим указанный несобственный интеграл. Имеем
ведут себя одинаково относительно сходимости. Рассмотрим указанный несобственный интеграл. Имеем
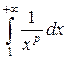
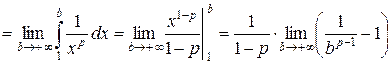 .
.
Так как по условию 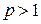 , то
, то 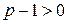 . Но тогда
. Но тогда 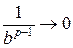 при
при 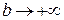 и
и 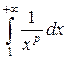
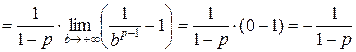 .
.
Итак, получили, что несобственный интеграл 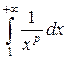 при
при 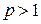 сходится. Следовательно, ряд
сходится. Следовательно, ряд 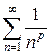 (
(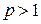 ) тоже сходится.
) тоже сходится.
Пример 18. Исследуем сходимость ряда 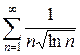 интегральным признаком Коши.
интегральным признаком Коши.
По формуле общего члена введем функцию 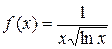 . Она непрерывна и монотонно убывает на промежутке
. Она непрерывна и монотонно убывает на промежутке  . Вычислим несобственный интеграл
. Вычислим несобственный интеграл
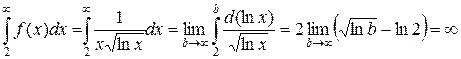 .
.
Интеграл расходится, поэтому расходится и ряд.
При исследовании сходимости ряда  с положительными членами иногда используется метод выделения главной части. Он применяется там, где удается получить с помощью формулы Тейлора асимптотическую формулу вид
с положительными членами иногда используется метод выделения главной части. Он применяется там, где удается получить с помощью формулы Тейлора асимптотическую формулу вид 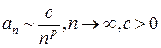 . В этом случае ряд
. В этом случае ряд  сходится или расходится одновременно с обобщенным гармоническим рядом
сходится или расходится одновременно с обобщенным гармоническим рядом 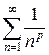 (см пример 17).
(см пример 17).
Пример 18. Исследовать на сходимость ряд 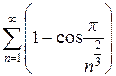 .
.
Так как  при
при 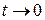 , то
, то
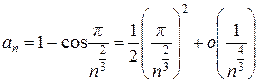 ,
,
откуда 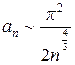 . Следовательно, ряд
. Следовательно, ряд 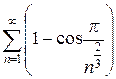 сходится.
сходится.
При оценке факториалов больших чисел и вычислении пределов, содержащих  бывает полезна формул Стиглинга:
бывает полезна формул Стиглинга:  , которая означает, что
, которая означает, что  .
.
Пример 19. Исследовать сходимость ряда 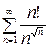 .
.
Применение признака Даламбера в данном случае затруднительно. Используем радикальный признак Коши и заменим  по формуле Стирлинга на
по формуле Стирлинга на  .
.
 .
.
Ряд расходится.
§3. Некоторые применения теория числовых рядов
1. Исследование сходимости несобственных интегралов с бесконечными пределами основано на использовании интегрального признака Коши.
Пример 1. Исследовать на сходимость 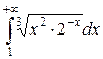 .
.
Функция 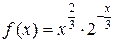 непрерывна и положительна для
непрерывна и положительна для 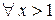 . Составим ряд
. Составим ряд  . Он сходится по признаку Даламбера, так как
. Он сходится по признаку Даламбера, так как
 .
.
Из сходимости ряда вытекает сходимость данного интеграла.
2. Достаточные признаки можно использовать для доказательства равенств вида 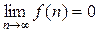 .
.
Пример 2. Доказать, что  . Обозначим
. Обозначим 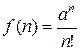 ,
, 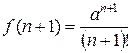 . Составим ряд
. Составим ряд 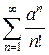 . Исследуем его сходимость признаком Даламбера:
. Исследуем его сходимость признаком Даламбера:
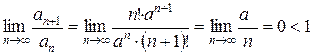 .
.
Так как ряд с общим членом 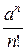 сходится, то
сходится, то 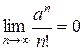 по необходимому признаку сходимости.
по необходимому признаку сходимости.
|