Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Флегмовое число
|
|
МАТЕРИАЛЬНЫЙ БАЛАНС КОЛОННЫ
Материальный баланс колонны
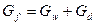 ,
,
где Gf – расход свежей смеси;
Gw – расход кубовых остатков;
Gd – расход готовой продукции.
Уравнение материального баланса для низкокипящего компонента:
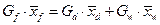 ,
,
где 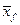 - молярная концентрация исходной смеси в жидкой фазе;
- молярная концентрация исходной смеси в жидкой фазе;
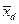 - молярная концентрация дистиллята в жидкой фазе;
- молярная концентрация дистиллята в жидкой фазе;
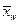 - молярная концентрация кубовых остатков в жидкой фазе.
- молярная концентрация кубовых остатков в жидкой фазе.
Определяется массовая концентрация низкокипящего компонента в исходной смеси, в дистилляте, кубового остатка по формуле:
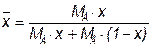 ,
,
где 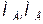 - молекулярные массы низкокипящего и низкокипящего компонентов соответственно.
- молекулярные массы низкокипящего и низкокипящего компонентов соответственно.
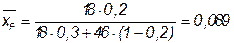
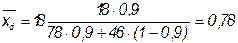
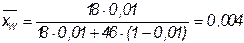
Составим систему уравнений из (2.1) и (2.2):
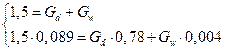
Решив систему уравнений, получим:
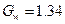 кг/с.
кг/с.
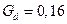 кг/с.
кг/с.
ФЛЕГМОВОЕ ЧИСЛО
Работа колонны в большой степени зависит от величины флегмового числа:
 ,
,
где 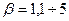 - коэффициент избытка флегмы.
- коэффициент избытка флегмы.
Минимальное флегмовое число:
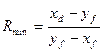 ,
,
где 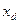 - молярная концентрация дистиллята в жидкой фазе;
- молярная концентрация дистиллята в жидкой фазе;
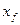 - молярная концентрация исходной смеси в жидкой фазе;
- молярная концентрация исходной смеси в жидкой фазе;
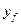 - молярная концентрация исходной смеси в паровой фазе.
- молярная концентрация исходной смеси в паровой фазе.
 2.3 ОПРЕДЕЛЕНИЕ ЧИСЛА ТАРЕЛОК
2.3 ОПРЕДЕЛЕНИЕ ЧИСЛА ТАРЕЛОК
Определяется теоретическое число тарелок, при котором обеспечивается полное физическое равновесие между стекающей с тарелки жидкостью и поднимающимся паром при равномерном распределении пара по сечению тарелки.
2.3.1. Построение диаграммы фазового равновесия y=f(x, y)
Задаваясь значением температур в промежутке от tA до tB, из уравнения Антуана определяют давления насыщения низкокипящего компонента при данных температурах:
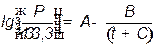 ,
,
где t – температура насыщения компонента смеси, оC;
А, В, С – коэффициенты пропорциональности (для воды: А=8, 07414 В=1733 С=233, 84). Для этилового спирта:

Мольные концентрации низкокипящего компонента в жидкой фазе определяются по формуле:
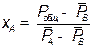 ,
,
где Pобщ – общее давление смеси, Па. Принимаем равным давлению при нормальных условиях 101325 Па.
Используя закон Рауля, определяют концентрации низкокипящего компонента в паровой фазе в интервале температур от tA до tB:
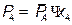 ,
,
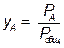 ,
,
где PA – парциальное давление низкокипящего компонента при температуре ti, Па.
Равновесные молекулярные доли жидкости (х) и пара (y) и температуры кипения смеси уксусная кислота – вода приведены в таблице 2.1.
Таблица 2.1.
| t, 0C | 78, 3 | ||||||
| PA, МПа | 107321, 8 | 125327, 6 | 145747, 4 | 168814, 4 | 194773, 4 | 223880, 0 | |
| PB, МПа | 47538, 8 | 55788, 1 | 65208, 9 | 75929, 2 | 88086, 1 | 101826, 5 | |
| XA, % | 0, 900 | 0, 655 | 0, 448 | 0, 273 | 0, 124 | ||
| yA, % | 0, 953 | 0, 810 | 0, 645 | 0, 456 | 0, 239 |
Строим фазовую диаграмму и диаграмму равновесия бинарной смеси метиловый спирт-вода.
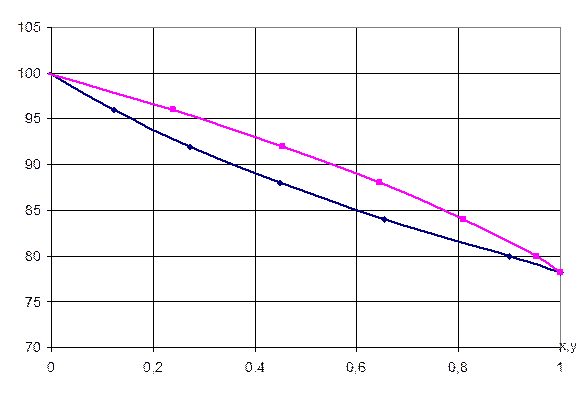
Рисунок 2.1 – Фазовая диаграмма бинарной смеси этиловый спирт-вода
2.3.2. Построение диаграммы фазового равновесия y=f(x)
Равновесные (сопряженные) концентрации компонента А в жидкой и газообразных фазах находятся на изотерме, пересекающей соответствующие линии испарения и конденсации,  поэтому берутся эти значения (xi и yi) и наносятся на диаграмму в координатах y=f(x) (рисунок 2.2).
поэтому берутся эти значения (xi и yi) и наносятся на диаграмму в координатах y=f(x) (рисунок 2.2).
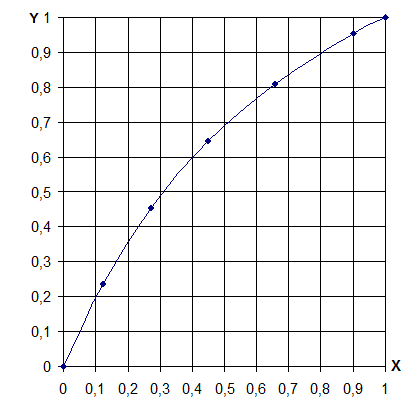
Рисунок 2.2 – Диаграмма фазового равновесия y=f(x)
2.3.3. Построение диаграммы фазового равновесия h=f(x, y)
В диапазоне температур кипения чистых компонентов определяют энтальпию кипящей жидкости по формуле, кДж/кг:
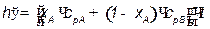 ,
,
где 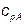 и
и 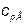 – изобарные теплоемкости низкокипящего и высококипящего компонентов соответственно, кДж/кг∙. Для воды
– изобарные теплоемкости низкокипящего и высококипящего компонентов соответственно, кДж/кг∙. Для воды 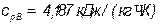 , для этилового спирта
, для этилового спирта 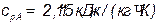 .
.
В диапазоне температур кипения чистых компонентов определяют энтальпию насыщенного пара по формуле, кДж/кг:

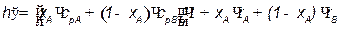
где 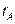 ,
, 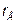 - скрытая теплота парообразования, кДж/кг. Для воды
- скрытая теплота парообразования, кДж/кг. Для воды  ,
,
для этилового спирта 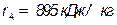 .
.
Результаты вычислений энтальпии кипящей жидкости и энтальпии насыщенного пара приведены в таблице – 2.2.
Таблица 2.2.
| t, 0C | 78, 3 | ||||||
| h', кДж/кг | 165, 6 | 185, 827 | 237, 7353 | 286, 69062 | 333, 0854 | 377, 2689 | 418, 7 |
| h", кДж/кг | 1217, 75 | 1603, 8857 | 1934, 5803 | 2219, 88 | 2467, 886 | 2678, 7 |
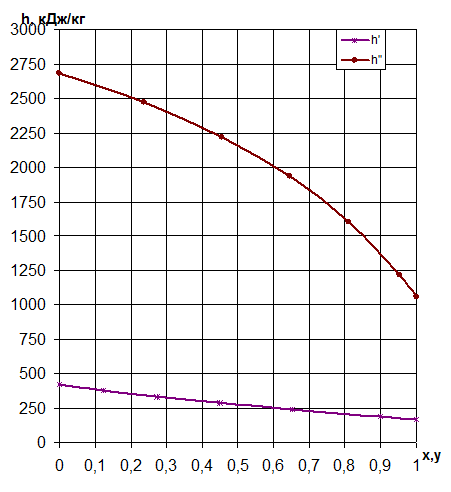
Рисунок 2.3 – Диаграмма фазового равновесия 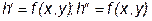
2.3.4. Графический метод определения теоретического числа тарелок методом Мак-Кэба-Тиле
Используя допущение, которое гласит, что в дефлегматоре не происходит изменения состава пара, то есть 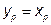 , значение концентрации
, значение концентрации 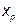 выносится на диагональ. Отмечается точка а (
выносится на диагональ. Отмечается точка а (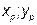 ) (рисунок 2.4).
) (рисунок 2.4).
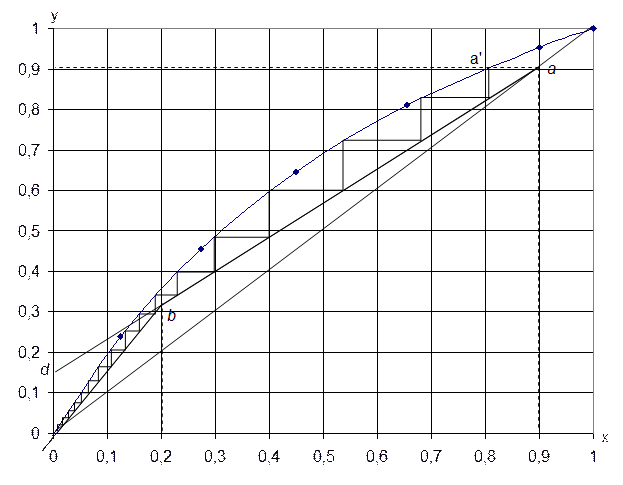
Рисунок 2.4 - Диаграмма равновесия бинарной смеси этиловый спирт-вода
 На диаграмме равновесия отмечаются молярные концентрации компонентов в жидкой фазе
На диаграмме равновесия отмечаются молярные концентрации компонентов в жидкой фазе 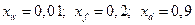 . Им соответствуют молярные концентрации компонентов в паровой фазе
. Им соответствуют молярные концентрации компонентов в паровой фазе 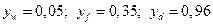 .
.
Определяется минимальное значение флегмового числа:

Флегмовое число влияет на величину капитальных и эксплуатационных затрат. С увеличением флегмового числа уменьшается число тарелок в колонне, но увеличиваются расход веществ и диаметр колонны. Поэтому необходимо рассчитать оптимальное флегмовое число:
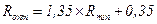

Расчётное уравнение рабочей линии, или линии изменения концентрации в колонне, для верхней (укрепляющей части) колонны:
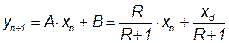 ,
,
где  – содержание низкокипящего компонента в паре, поднимающимся с последующей тарелки;
– содержание низкокипящего компонента в паре, поднимающимся с последующей тарелки;
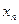 – содержание низкокипящего компонента в жидкости на данной тарелке.
– содержание низкокипящего компонента в жидкости на данной тарелке.
На диаграмме 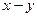 откладываем отрезок ОМ = В.
откладываем отрезок ОМ = В.
 .
.
Счёт тарелок осуществляется сверху вниз.
Отмечается точка d (0, В) и через точки а и d проводится рабочая линия укрепляющей части колонны. На эту рабочую линию выносится значение концентрации низкокипящего компонента 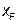 в исходной смеси и отмечается точка b. Эта точка характеризует концентрацию низкокипящего компонента на питательной тарелке (рисунок 2.2). Следовательно, точка b является исходной точкой построения рабочей линии исчерпывающей части колонны.
в исходной смеси и отмечается точка b. Эта точка характеризует концентрацию низкокипящего компонента на питательной тарелке (рисунок 2.2). Следовательно, точка b является исходной точкой построения рабочей линии исчерпывающей части колонны.
Используя допущение, что при испарении жидкости в кипятильнике не происходит изменения ее состава, то есть состав пара, образующегося в кипятильнике, соответствует составу кубового остатка (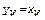 ), значение концентрации низкокипящего компонента в жидкой фазе куба колонны выносится на диагональ и отмечается точка с. Через точку с и точку b проводится рабочая линия исчерпывающей части колонны.
), значение концентрации низкокипящего компонента в жидкой фазе куба колонны выносится на диагональ и отмечается точка с. Через точку с и точку b проводится рабочая линия исчерпывающей части колонны.
 На тарелке происходит
На тарелке происходит 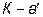 конденсации и парообразования, выражающийся ступенью
конденсации и парообразования, выражающийся ступенью 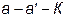 (рисунок 2.2). Количество таких ступеней до точки b определяет число теоретических тарелок в укрепляющей части колонны (6 тарелок). Количество ступеней от точки b до точки с дают число теоретических тарелок в укрепляющей части колонны (10 тарелок).
(рисунок 2.2). Количество таких ступеней до точки b определяет число теоретических тарелок в укрепляющей части колонны (6 тарелок). Количество ступеней от точки b до точки с дают число теоретических тарелок в укрепляющей части колонны (10 тарелок).
2.3.5. Графический метод Меркеля в координатах h=f(x, y). Определение теоретического числа тарелок
Определяется удельный тепловой поток в конденсаторе по формуле:
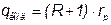 , hрррр
, hрррр
где 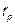 - скрытая теплота фазового перехода дистиллята, которая определяется по формуле, кДж/кг:
- скрытая теплота фазового перехода дистиллята, которая определяется по формуле, кДж/кг:
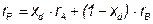 ,
,
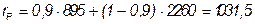 кДж/кг
кДж/кг
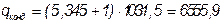 кДж/кг
кДж/кг

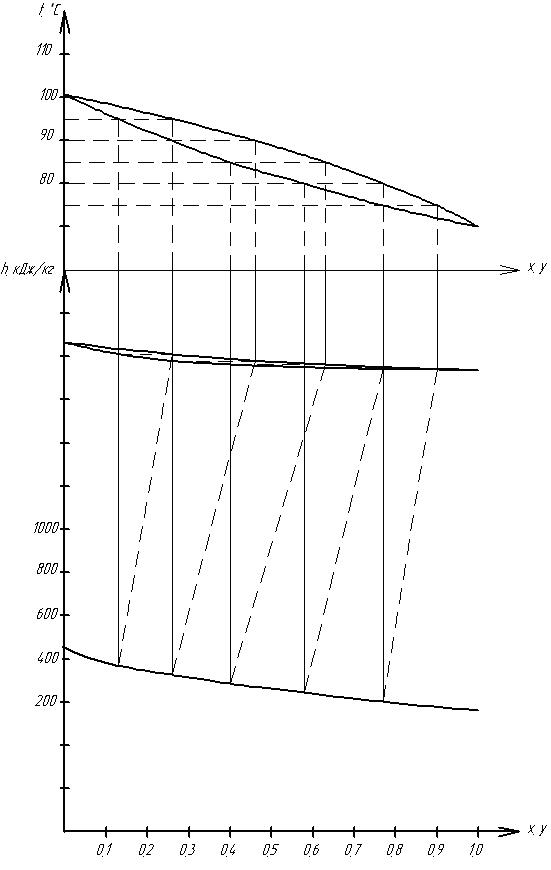
Рисунок 2.5 – Построение вспомогательной линии

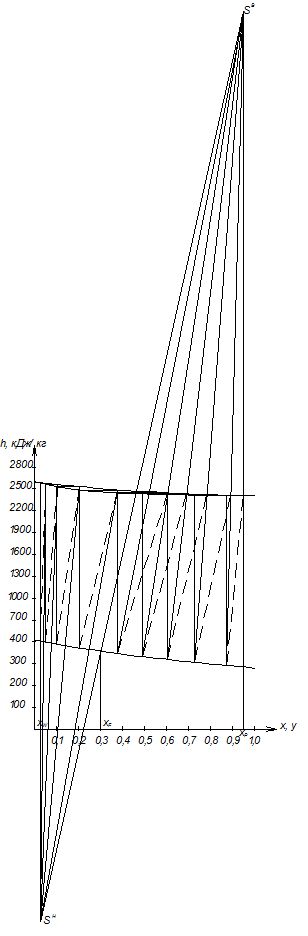
Рисунок 2.6 – Определение числа тарелок по графическому методу Меркеля в координатах h=f(x, y)
2.4.  ОПРЕДЕЛЕНИЕ РАЗМЕРОВ КОЛОННЫ
ОПРЕДЕЛЕНИЕ РАЗМЕРОВ КОЛОННЫ
2.4.1. Уравнения рабочих линий
В верхней части колонны
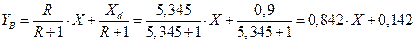
В нижней части колонны
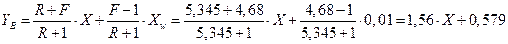
2.4.2. Относительный мольный расход питания
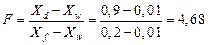
2.4.3. Средние концентрации жидкости
В верхней части колонны
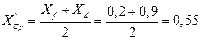
В нижней части колонны
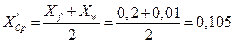
2.4.4. Средние концентрации пара находим по уравнениям рабочих линий
В верхней части колонны
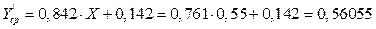
В нижней части колонны
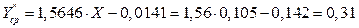
2.4.5. Средняя молекулярная доля пара в колонне
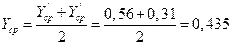
По фазовой диаграмме t-X, Y находим, что величине Yср=0, 435 соответствует температура пара
tП=930С
2.4.6. Средняя мольная масса смеси при данной температуре

2.4.7. Средняя плотность пара
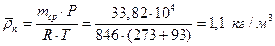
2.4.8. Объемный расход, проходящего через колонну пара при средней температуре
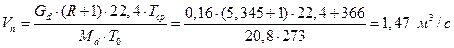 ,
,
где Мd – мольная масса дистиллята
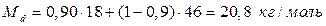
2.4.9. Средняя плотность жидкости в колонне
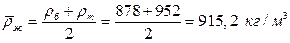
2.4.10.  Объемный расход жидкости в нижней и верхней части колонны
Объемный расход жидкости в нижней и верхней части колонны
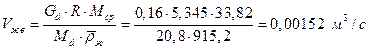
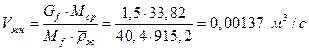 ,
,
где 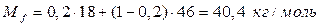
2.4.11. Примем расстояние между тарелками
НТ=300 мм
DК=0, 8 м.
2.4.12. Скорость пара в колонне
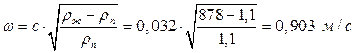
2.4.13. Расчетная скорость пара
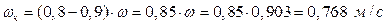
2.4.14. Диаметр колонны

2.4.15. Принимаем тарелку типа ТС-Р
НТ=450 мм
DК=1600 мм
2.4.16. Уточняем действительную скорость пара в колонне
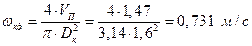
2.4.17. Определение высоты колонны