
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решения задач диагностической работы
|
|
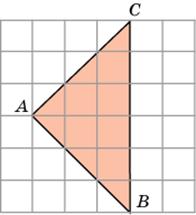
1. Первое решение. Заметим, что данный треугольник ABC является прямоугольным ( 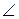 A = 90о). Воспользуемся тем, что диагональ квадратной клетки со сторонами, равными 1, равна
A = 90о). Воспользуемся тем, что диагональ квадратной клетки со сторонами, равными 1, равна 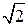 . Тогда катеты AB и AC данного треугольника будут равны
. Тогда катеты AB и AC данного треугольника будут равны 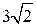 . Так как площадь прямоугольного треугольника равна половине произведения его катетов, то площадь данного треугольника будет равна
. Так как площадь прямоугольного треугольника равна половине произведения его катетов, то площадь данного треугольника будет равна 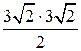 , т.е. равна 9.
, т.е. равна 9.
 |
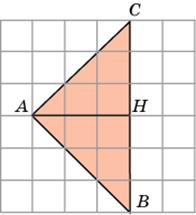
Второе решение. Проведем высоту AH. Тогда BC = 6, AH = 3 и, следовательно, 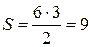 .
.
 |
Ответ. 9.
2. Первое решение. Так как диагональ квадрата со стороной 1 равна 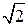 , то сторона AC треугольника ABC равна
, то сторона AC треугольника ABC равна  , высота BH, проведенная к этой стороне, равна
, высота BH, проведенная к этой стороне, равна  . Следовательно, площадь данного треугольника равна
. Следовательно, площадь данного треугольника равна 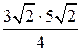 , т.е. равна 7, 5.
, т.е. равна 7, 5.
 |
Второе решение. Разобьем данный треугольник ABC на два треугольника ABD и BDC. Их общая сторона BD равна 3, а высоты, к ней проведенные, равны соответственно 1 и 4. Площадь треугольника ABD равна 1, 5, а площадь треугольника BDC равна 6. Площадь треугольника ABC равна сумме площадей этих треугольников и, следовательно, равна 7, 5.
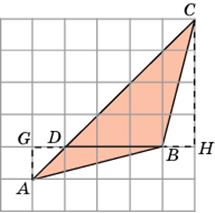 |
Ответ. 7, 5.
3. Первое решение. Найдем стороны данного прямоугольника. Рассмотрим прямоугольный треугольник ADE. Катет AE равен 4, катет DE равен 2. Следовательно, по теореме Пифагора гипотенуза AD равна 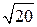 . Аналогично, для прямоугольного треугольника ABF катет AF равен 1, катет BF равен 2, Следовательно, по теореме Пифагора гипотенуза AB равна
. Аналогично, для прямоугольного треугольника ABF катет AF равен 1, катет BF равен 2, Следовательно, по теореме Пифагора гипотенуза AB равна  . Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного прямоугольника будет равна
. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного прямоугольника будет равна 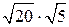 , т.е. равна 10.
, т.е. равна 10.
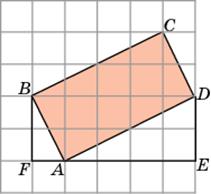 |
Второе решение. Разобьем данный прямоугольник ABCD на два треугольника ABD и BCD. Сторона BD у них общая и равна 5. Высоты AE и CF, опущенные на эту сторону, равны 2. Так как площадь треугольника равна половине произведения стороны на высоту, опущенную на эту сторону, то площадь каждого из этих двух треугольников будет равна 5 и, следовательно, площадь прямоугольника будет равна 10.
 |
Ответ. 10.
4. Первое решение. Напомним, что площадь ромба равна половине произведения его диагоналей. Воспользуемся тем, что диагональ квадратной клетки со сторонами, равными 1, равна 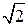 . Тогда диагонали AС и BD данного ромба будут равны соответственно
. Тогда диагонали AС и BD данного ромба будут равны соответственно 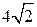 и
и 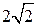 , а его площадь будет равна
, а его площадь будет равна 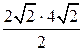 , т.е. равна 8.
, т.е. равна 8.
 |
Второе решение. Достроим на сторонах ромба четыре равных прямоугольных треугольника, катеты которых равны 1 и 3. Площадь каждого такого треугольника равна 1, 5. Ромб вместе с этими треугольниками образует фигуру, состоящую из четырнадцати единичных квадратов. Следовательно, ее площадь равна 14. Вычитая из нее площадь четырех треугольников, получим, что площадь ромба равна 8.
 |
Ответ. 8.
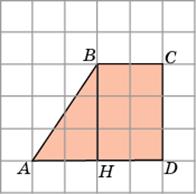
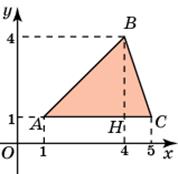
5. Первое решение. Основания AD и BC данной трапеции равны соответственно 4 и 2. Высотой является боковая сторона CD. Она равна 3.Так как площадь трапеции равна произведению полусуммы оснований на высоту, то площадь данной трапеции будет равна  , т.е. равна 9.
, т.е. равна 9.
 |
Второе решение. Из точки B опустим перпендикуляр BH на AD. Он разобьет трапецию на прямоугольный треугольник ABH и прямоугольник HBCD. Катеты прямоугольного треугольника равны 2 и 3, следовательно, его площадь равна 3. Смежные стороны прямоугольника равны 2 и 3, следовательно, его площадь равна 6. Площадь трапеции равна сумме площадей треугольника и прямоугольника и, следовательно, равна 9.
 |
Ответ. 9.
6. Первое решение. Основания AD и BC трапеции равны соответственно 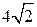 и
и 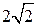 . Высота BH трапеции равна
. Высота BH трапеции равна  . Так как площадь трапеции равна произведению полусуммы оснований на высоту, то площадь данной трапеции будет равна
. Так как площадь трапеции равна произведению полусуммы оснований на высоту, то площадь данной трапеции будет равна 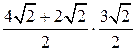 и, следовательно, будет равна 9.
и, следовательно, будет равна 9.
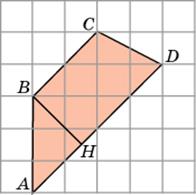 |
Второе решение. Разобьем трапецию на параллелограмм ABCE и треугольник CDE. Сторона AB параллелограмма ABCE равна 3, высота EH, к ней проведенная, равна 2, следовательно, площадь этого параллелограмма равна 6. Сторона CE треугольника CDE равна 3, высота DG, к ней проведенная, равна 2, следовательно, площадь этого треугольника равна 3. Площадь трапеции равна сумме площадей параллелограмма и треугольника и, следовательно, равна 9.
 |
Ответ. 9.
7. Первое решение. Разобьем данный четырехугольник на два треугольника ABC и ACD. Сторона AC у них общая и равна 4. Высоты BH и DH равны 2. Следовательно, площади этих треугольников равны 4 и, значит, площадь четырехугольника равна 8.
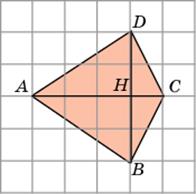 |
Второе решение. Разобьем данный четырехугольник на два треугольника ABD и BCD. Сторона BD у них общая и равна 4. Высоты AH и CH равны соответственно 3 и 1. Следовательно, площади этих треугольников равны соответственно 6 и 2. Значит, площадь четырехугольника равна 8.
Ответ. 8.
 |
8. Первое решение. Разобьем данный четырехугольник на два треугольника ACB и ACD. Сторона AC у них общая и равна
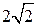 . Высоты BH и DH равны
. Высоты BH и DH равны  . Следовательно, площади этих треугольников равны 3. Значит, площадь четырехугольника равна 6.
. Следовательно, площади этих треугольников равны 3. Значит, площадь четырехугольника равна 6.
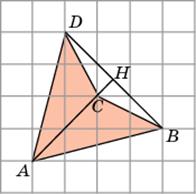 |
Второе решение. Площадь данного четырехугольника равна разности площадей треугольников ABD и CBD. В треугольнике ABD сторона BD равна
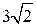 , высота AH равна
, высота AH равна 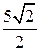 . Следовательно, его площадь равна 7, 5. В треугольнике CBD сторона BD равна
. Следовательно, его площадь равна 7, 5. В треугольнике CBD сторона BD равна 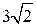 , высота CH равна
, высота CH равна 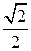 . Следовательно, его площадь равна 1, 5. Таким образом, площадь данного четырехугольника равна 6.
. Следовательно, его площадь равна 1, 5. Таким образом, площадь данного четырехугольника равна 6.
Ответ. 6.
9. Первое решение. Напомним, что площадь S кругового сектора вычисляется по формуле 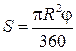 , где R – радиус круга,
, где R – радиус круга, 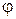 - градусная величина угла сектора. В нашем случае
- градусная величина угла сектора. В нашем случае 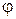 = 90о. Радиус R равен
= 90о. Радиус R равен  . Подставляя данные значения R и
. Подставляя данные значения R и 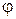 в формулу площади сектора, получим S =
в формулу площади сектора, получим S = 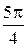 . Откуда
. Откуда 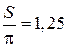 .
.
 |
Второе решение. Заметим, что данный сектор является одной четвертой частью круга и, следовательно, его площадь равна одной четвертой площади круга. Площадь круга равна
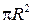 , где R – радиус круга. В нашем случае R =
, где R – радиус круга. В нашем случае R =  и, следовательно, площадь S сектора равна
и, следовательно, площадь S сектора равна 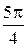 . Откуда
. Откуда 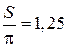 .
.
 |
Ответ. 1, 25.
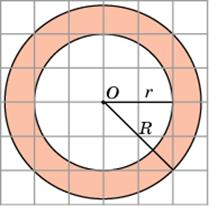
10. Площадь кольца равна разности площадей внешнего и внутреннего кругов. Радиус R внешнего круга равен 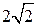 , радиус r внутреннего круга равен 2. Следовательно, площадь S кольца равна
, радиус r внутреннего круга равен 2. Следовательно, площадь S кольца равна 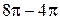 , т.е. S =
, т.е. S = 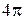 и, следовательно,
и, следовательно, 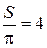 .
.
 |
Ответ. 4.
11. Из вершины B треугольника ABC опустим высоту BH. Она равна 3. Сторона AC равна 4. Следовательно, площадь треугольника равна 6.
Ответ. 6.
 |
12. Разобьем четырехугольник ABCD на два треугольника ABD и BCD. Высоты AG и CH этих треугольников, опущенные на сторону BD, равны2, сторона BD равна 5. Следовательно, площади этих треугольников равны 5 и, значит, площадь четырехугольника ABCD равна 10.
Ответ. 10.