
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Общие положения. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
|
|
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
" Ижевский государственный технический университет имени М.Т. Калашникова"
(ФГБОУ ВПО «ИжГТУ имени М.Т. Калашникова»)
Сергей Петрович Сырыгин
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ
ПО ДИСЦИПЛИНЕ
«МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ»
для студентов направления: 080100.62 «Экономика», профиль «Финансы и кредит»
Рекомендовано учебно-методическим советом ФГБОУ ВПО «ИжГТУ имени М.Т. Калашникова» для использования в учебном процессе в качестве методических указаний для студентов обучающихся по направлению 080100.62 «Экономика», профиль «Финансы и кредит» при изучении дисциплины «Методы оптимальных решений»
Ижевск 2013
УДК 336.763
Составитель: к.т.н., доцент. С.П. Сырыгин
Рецензент: к.т.н., профессор. В.А.Галашев
Методические указания по выполнению курсовой работы по дисциплине «Методы оптимальных решений» для студентов направления 080100.62 «Экономика», профиль «Финансы и кредит». – Ижевск, 2013. – 20с.
Рекомендовано к изданию на заседании кафедры «Финансы и кредит» 5.07.2013г., протокол №21
СОДЕРЖАНИЕ
1. Общие положения……………………………………………………..4
2. Структура, содержание и объем курсовой работы………………….5
3. Заключение……………………………………………………………15
4. Подготовка к защите и защита работы……………………………...16
5. Перечень контрольных вопросов для самоконтроля……………….17
6. Список используемой литературы ……...............................................19
ОБЩИЕ ПОЛОЖЕНИЯ
Курсовая работа представляет собой весьма эффективный вид самостоятельной подготовки студента и является учебно-научной работой.
Целью работы является получение и применение знаний и умений, полученных в процессе обучения и закрепления навыков самостоятельной работы с фактическим материалом по выбранной теме.
В процессе выполнения, исходя из цели, студент решает следующие задачи:
- выбор темы, обоснование актуальности, исходя из проблемной ситуации;
- подбор литературных источников, законодательных актов по теме;
- поиск и статистическая обработка фактической информации с целью выявления общих тенденций и закономерностей, и уточнение проблемной ситуации;
- изучение по научной литературе средств и методов выявленной проблемы;
- моделирование различных вариантов решения проблемы и выбор оптимального решения;
Исходя из содержания изучаемой дисциплины, курсовая работа должна содержать разделы, включающие модели рынка ценных бумаг, результаты моделирования, то есть носить расчетно – аналитический характер.
Курсовая работа представляет собой самостоятельное научное исследование, и роль руководителя должна в основном сводиться к консультированию по методическим вопросам.
Сроки выполнения всех этапов, а также защиты, согласуются с руководителем в соответствии с решениями кафедры.
СТРУКТУРА, СОДЕРЖАНИЕ И ОБЪЕМ КУРСОВОЙ РАБОТЫ
Курсовая работа, как правило, должна содержать введение, 2-3 главы, заключение и список использованной литературы. В работах, не содержащих большого объема расчетов, возможно изложение основного материала в рамках 2-х глав.
Введение содержит 2…3 страницы машинописного текста. Во введении необходимо обосновать актуальность выбранной темы, сформулировать цель и поставить задачи, решение которых будет отражено в каждой главе работы. Необходимо указать объект и предмет исследования, обозначить хронологические рамки и соответствующую информационную базу исследования.
Основное назначение первой главы – более конкретно обозначить и уточнить основные проблемы, которые должны быть решены в процессе выполнения курсовой работы, а также исследуются теоретические аспекты поставленной проблемы, в связи с этим, необходимо более полно раскрыть актуальность, практическую значимость, дать более полную характеристику исследуемого объекта (предприятия, отрасли, сегмента рынка и т.д.).
Для решения задач, стоящих в первой главе, следует дать характеристику эмитента ценных бумаг, используемых инструментов, особенностей функционирования рынка ценных бумаг на исследуемом временном интервале, провести анализ основных финансово-экономических характеристик в динамике за 3 периода. Целесообразно, если автор подтверждает актуальность, решаемые проблемы и задачи мнением известных специалистов в исследуемой области.
Уровень обоснованности выводов по первой главе будет выше, если автор подтвердит их собственными аналитическими выкладками, основанными на количественном моделировании. При рассмотрении теоретических аспектов важно показать подходы не только отечественной науки, но и взгляды зарубежных ученых, учитывая их большой вклад в создание моделей рынка ценных бумаг.
При работе над второй главой необходимо использовать все имеющиеся источники информации: законодательные акты, учебники и учебные пособия, монографии, научные статьи. Важными источниками информации являются международная сеть Internet, информационно – справочные системы «Консультант +», «Гарант».
Вторая глава носит расчетно-аналитический характер. В этой главе требуется произвести оптимизацию инвестиционного портфеля используя метод линейного программирования, обосновать оптимальный по выбранным критериям вариант. Выбор оптимального варианта должен базироваться на математической модели и включать несколько этапов.
На первом этапе требуется осуществить прогнозирование ситуации на рынке (как правило, в виде цен исследуемых активов и показателя фондового индекса). Прогноз может базироваться на гипотезе о сохранении закономерностей движения цен активов и индекса проявившееся на интервале ретроспекции. Обоснование предложений, направленных на решение сформулированных проблем, как правило, базируется на поиске оптимума по выбранному критерию. В качестве критерия оптимизации может быть выбран риск или доходность портфеля. Важным моментом при осуществлении моделирования исследуемого объекта является установление разумных ограничений, в которых модель адекватна объекту с требуемым уровнем точности. Выбор активов и ограничений студент может осуществить самостоятельно или по рекомендации преподавателя. Нередко студентом совершается ошибка, заключающаяся в том, что результаты моделирования распространяются за пределы ограничений, что, очевидно, ведет к ошибочным выводам.
Поиск оптимального решения сводится к задаче линейного программирования. Задача линейного программирования состоит в том, что необходимо максимизировать или минимизировать некоторый линейный функционал на многомерном пространстве при заданных линейных ограничениях.
Каждое из линейных неравенств на переменные ограничивает полупространство в соответствующем линейном пространстве. В результате все неравенства ограничивают некоторый многогранник (возможно, бесконечный), называемый также полиэдральным комплексом. Уравнение W(x) = c, где W(x) — максимизируемый (или минимизируемый) линейный функционал, порождает гиперплоскость L(c). Зависимость от c порождает семейство параллельных гиперплоскостей. Тогда экстремальная задача приобретает следующую формулировку — требуется найти такое наибольшее c, что гиперплоскость L(c) пересекает многогранник хотя бы в одной точке. Пересечение оптимальной гиперплоскости и многогранника будет содержать хотя бы одну вершину, причём, их будет более одной, если пересечение содержит ребро или k-мерную грань. Поэтому максимум функционала можно искать в вершинах многогранника
Алгоритм решения Симплекс-методом оптимизационной задачи линейного программирования осуществляется путём перебора вершин выпуклого многогранника в многомерном пространстве. Методика линейного программирования была разработана Д. Данцигом в 1947 году.
Идея симплекс-метода состоит в том, что выбирается одна из вершин многогранника, после чего начинается движение по его рёбрам от вершины к вершине в сторону увеличения значения функционала. Когда переход по ребру из текущей вершины в другую вершину с более высоким значением функционала невозможен, считается, что оптимальное значение c найдено.
Последовательность вычислений симплекс-методом можно разделить на два этапа:
1)нахождение исходной вершины множества допустимых решений,
2)последовательный переход от одной вершины к другой, ведущий к оптимизации значения целевой функции.
При этом в некоторых случаях исходное решение очевидно или его определение не требует сложных вычислений, например, когда все ограничения представлены неравенствами вида «меньше или равно» (тогда нулевой вектор совершенно точно является допустимым решением, хотя и, не всегда, далеко не оптимальным).
Симплекс-метод является универсальным то есть может быть использован при любом количестве независимых переменных. Симплекс-метод реализуется путём перехода от одной вершины пространственного многогранника к другой при условии, что значение целевой функции должно увеличиваться или не уменьшаться.
Для реализации симплекс-метода необходимо перевести систему ограничений из стандартной формы в каноническую, то есть преобразовать ограничения в виде неравенств в ограничения в форме равенств.
Процесс применения симплекс-метода предполагает решение 3-х элементов:
1. Способ определения какого-либо базисного решения;
2. Правило перевода к лучшему решению;
3. Способ и критерий проверки оптимальности найденного решения.
Алгоритм решения задачи с помощью симплекс-метода представлен на Рис 1.
|
|
|
|



|

|



|
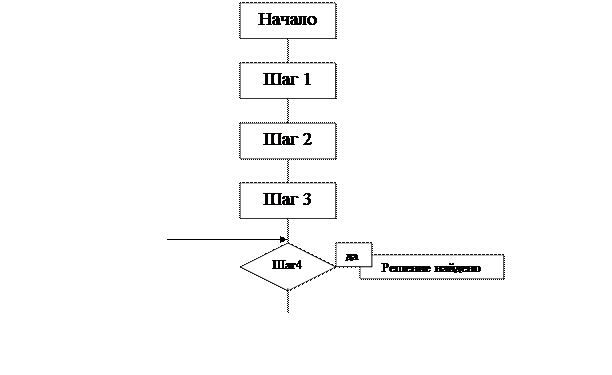
Рис.1. Алгоритм решения задачи симплекс-методом
Содержание шагов:
Шаг 1 Формулировка целевой функции и системы ограничений.
F(x) = 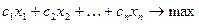
или
F(x) = - (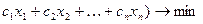
g(x) = 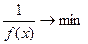 (f(x)> 0)
(f(x)> 0)
Система ограничений:
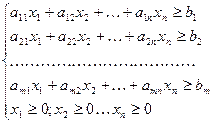
Шаг 2 Приведение задачи к канонической форме (перевод ограничений в виде неравенств в ограничения в виде равенств). Для этого вводим дополнительные переменные.
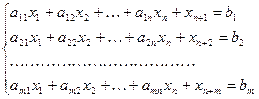
Шаг 3 Построение исходной симплекс-таблицы. Получение первоначального допустимого базисного решения.
В качестве допустимого базисного решения целесообразно взять решение, в котором основными являются дополнительные переменные.
Таблица 6. Исходная симплекс-таблица
| Базис | Переменные | |||||||
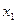
| 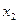
| 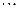
| 
| 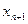
| 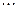
| 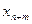
| bj 
| |
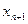
| 
| 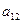
| … | 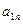
| b1 | |||
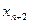
| 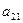
| 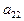
| … | 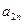
| b2 | |||
| … | … | … | … | … | … | … | … | … |
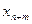
| 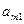
| 
| … | 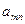
| bm | |||

| 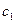
| 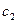
| … | 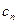
| -f(x) |
Целевая функция будет выглядеть так:
F(x) = 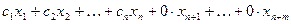
Шаг 4 Проверка условия, что все  . Если это условие выполняется, то решение найдено. В случае обратного переходим к следующему шагу.
. Если это условие выполняется, то решение найдено. В случае обратного переходим к следующему шагу.
Шаг 5 Выбор разрешающего столбца, соответствующего переменной, которую необходимо ввести в базис. Разрешающий столбец соответствует максимальному значению коэффициента  .
.

Шаг 6 Проверка условия, что все элементы разрешающего столбца 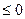

При выполнении этого условия целевая функция неограниченна и решения нет. При невыполнении условия – переход к шагу 7.
Шаг 7 Выбор разрешающей строки, то есть выбор переменной, которую необходимо убрать из базиса.

Минимальное значение этого решения будет соответствовать строке, которую необходимо заменить. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки называется разрешающим элементом.
Шаг 8 Пересчёт элементов симплекс-таблицы.
i – номер строки
j – номер столбца
r – номер разрешающего столбца
s – номер разрешающей строки
Все элементы разрешающего столбца, кроме разрешающего элемента принимаются равными 0.
Приведённые формулы используются для формирования новой симплекс-таблицы
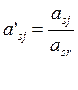
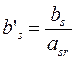
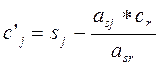
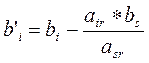


Порядок выполнения работы:
1. Предварительный выбор ценных бумаг, как представителей различных отраслей экономики. При выборе необходимо учесть требование высокой ликвидности. Окончательный выбор согласуется с преподавателем – руководителем курсовой работы.
2. Скачать с сайта «FINAM» дневные цены выбранных активов за срок 1 год, начиная с текущего дня в формате «csv».
3. Заменить разделитель десятичную точку на десятичную запятую.
4. вычислить дневные доходности по формуле Ri =ln(Pi+1 /Pi), где
Pi+1 – текущая цена актива;
Pi - цена актива за прошлый день.
5. С помощью «Пакета анализа» получить корреляционную и ковариационную матрицы по полученным доходностям.
6. Выбрать для формирования портфеля 3 актива, имеющие минимальные относительно друг друга значения корреляционной связи.
7. Произвести оптимизацию портфеля по критерию максимальной доходности. Доходность портфеля (Rp) определяем по формуле: 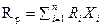 , где
, где
Ri - доходность i-го актива.
n – количество активов в портфеле;
Xi – доля i-го актива в портфеле;
За показатель риска следует взять 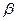 - коэффициент ценной бумаги,
- коэффициент ценной бумаги,
Для расчета 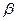 - коэффициента нужно рассчитать ковариационную и корреляционную матрицы по полученным доходностям с помощью «Пакета анализа». Для вычисления
- коэффициента нужно рассчитать ковариационную и корреляционную матрицы по полученным доходностям с помощью «Пакета анализа». Для вычисления 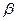 i следует использовать формулу:
i следует использовать формулу: 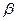 i =
i = 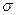 iI/
iI/ 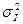 , где
, где
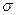 iI - ковариация доходностей i-го актив и индекса ММВБ.
iI - ковариация доходностей i-го актив и индекса ММВБ.
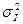 - дисперсия индекса ММВБ.
- дисперсия индекса ММВБ.
Риск портфеля определяется по формуле: 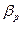 =
= 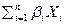 .
.
В качестве ограничений следует принять:
1. Не отрицательность долей активов в портфеле;
2. Ограничение на величину риска, которое согласовывается с руководителем курсовой работы;
3.Сумма долей активов в портфеле должна быть равной 1.
В результате выполнения курсовой работы студент должен знать методы решения задач линейного программирования; уметь сформулировать целевую функцию и ограничения на располагаемые ресурсы; иметь навыки поиска оптимума с использованием Симплекс-метода.
Примерный план курсовой работы « Оптимизация фондового портфеля по данным цен активов компаний.».
Введение.
Глава 1. Характеристика предприятия (отрасли, сектора финансового рынка), достигнутый уровень и результаты его деятельности.
1.1. Краткая историческая справка. Этапы создания и развития предприятия.
1.2. Анализ положения на рынке. Характеристика товаров и услуг предприятия.
1.3. Основные показатели хозяйственной деятельности и динамика их развития.
Глава 2. Разработка оптимальной структуры инвестиционного портфеля с учетом ограничений.
2.1. Теоретические основы оптимизации по симплекс-методу.
2.2. Формирование целевой функции и ограничений на располагаемые ресурсы.
2.3. Оптимизация инвестиционного портфеля.
Заключение.
Список используемой литературы.
Приложения.