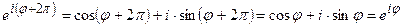Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение комплексных чисел
|
|
ЛЕКЦИЯ№3
КОМПЛЕКСНЫЕ ЧИСЛА
Определение комплексных чисел
Понятие комплексного числа возникло в связи с необходимостью решать квадратные уравнения при любых значениях дискриминанта, в том числе и отрицательных(XVIв):
x 2+4 x +13=0 D 1= 4 -13=-9.
При этом возникает необходимость расширения понятия числа, необходимость введения чисел более общей природы. Действительно числа уже будут частным случаем этих «новых» чисел.
Комплексным числом называется выражение z =x+iy, где x и y – действительные числа, а i – символ, который называется мнимой единицей: i 2 = -1.
Корни приведенного уравнения можно записать в виде
z 1 = (2+3 i), z 2 = (2-3 i).
Числа х и y называются, соответственно, действительной и мнимой частями комплексного числа z и обозначаются символами:
x = Re z, y = Im z
Если y = 0, z = x + i 0 считается совпадающим с действительным числом x. Если x = 0, то z = 0 + i y обозначается просто i y и называется чисто мнимым числом.
Выберем на плоскости декартову прямоугольную систему координат и будем рассматривать упорядоченную пару чисел (x, y) как координаты точек этой плоскости.
Тогда каждому числу z = x + iy будет отвечать определённая точка z (x, y) плоскости и, наоборот, каждой точке плоскости будет отвечать определённое число z = x + iy.
Таким образом, между множеством комплексных чисел и множеством точек плоскости Оху существует взаимно однозначное соответствие.
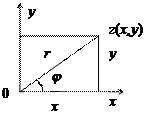 Плоскость Оху называется плоскостью комплексных чисел (z). Действительные числа изображаются при этом точками оси Oх. Ось Oх называется действительной осью. Чисто мнимые числа z = iy изображаются точками на оси Oу, которая называется мнимой осью.
Плоскость Оху называется плоскостью комплексных чисел (z). Действительные числа изображаются при этом точками оси Oх. Ось Oх называется действительной осью. Чисто мнимые числа z = iy изображаются точками на оси Oу, которая называется мнимой осью.
Рис.1.
1.2. Три формы записи комплексного числа
1. Алгебраическая форма:
z = x + iy. (1)
Два комплексных числа z 1 = x 1 + iy 1 и z 2 = x 2 + iy 2 равны друг другу (z 1 = z 2) тогда и только тогда, когда
x 1 = x 2, и y 1 = y 2
Если x 2 = x 1, а y 2 = - y 1, то комплексные числа z1 = z2 называются взаимно сопряжёнными:
z = x + iy,  = x – i y.
= x – i y.
Точки z (x, y) и z (x, -y) симметричны относительно действительной оси Oх.
2. Тригонометрическая форма.
Введём в рассмотрение радиус-вектор точки z и угол φ, образованный им с положительным направлением оси Oх. (рис.1).
Величины r и φ называются, соответственно, модулем и аргументом комплексного числа z и обозначаются символами:
r = | z |; φ = Arg z.
Модуль комплексного числа определяется однозначно формулой (из треугольника, рис 1);
r = | r | 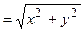
Все значения аргумента φ удовлетворяют соотношению
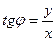 ,
, 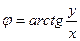
Угол φ называется аргументом комплексного числа z:
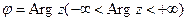
Аргумент определяется не однозначно, а с точностью до числа, кратного 2 π. Если z =0, то аргумент произволен.
Наименьшее по модулю значение аргумента Arg z называется его главным значением:
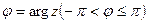 или
или 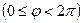

 , x > 0, y > 0;
, x > 0, y > 0;
 -
-  , x < 0, y > 0;
, x < 0, y > 0;
Arctg z =
 +
+  , x < 0, y < 0;
, x < 0, y < 0;
2  -
-  , x > 0, y < 0;
, x > 0, y < 0;
Главное значение аргумента определяется однозначно. Очевидно:
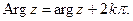
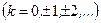
Из треугольника: x = 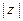 cos φ и y =
cos φ и y = 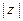 sin φ. Поэтому любое комплексное число можно записать в тригонометрической форме:
sin φ. Поэтому любое комплексное число можно записать в тригонометрической форме:
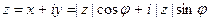 или (
или (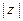 = r)
= r)
 (2)
(2)
Два комплексных числа z 1 и z 2 равны тогда и только тогда, когда равны их модули, а аргументы равны или отличаются на 2 кπ:
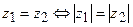 ;
; 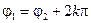
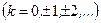
Для перехода от алгебраической формы (1) к тригонометрической (2) пользуются равенствами:
 ;
; 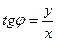
 ..
..
Примеры: Записать комплексные числа в тригонометри-
ческом виде
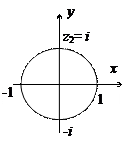
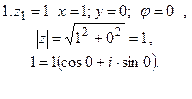
Рис.2.
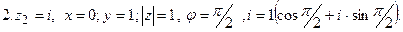
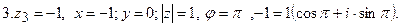
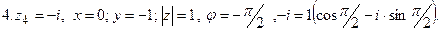
3. Показательная форма.
Рассмотрим показательную функцию с мнимым показателем  . Положим по определению:
. Положим по определению:
 = cos φ - i
= cos φ - i  - (формула Эйлера) (3)
- (формула Эйлера) (3)
Вывод этой формулы содержится в теории рядов. С её помощью от тригонометрической формы (2) записи комплексного числа можно перейти к показательной:
 (4)
(4)
Примеры: Записать комплексные числа в показательной форме.

Правая часть формулы (3) есть комплексное число с модулем, равным 1:


|
|
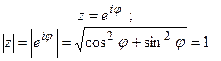 (5)
(5)
|

.
Рис. 3.
При φ =0 z =  =1; при φ =π /2 z=
=1; при φ =π /2 z= 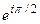 =I и т.д. Таким образом, при изменении φ от 0 до 2 π точки z =
=I и т.д. Таким образом, при изменении φ от 0 до 2 π точки z =  опишет окружность единичного радиуса против часовой стрелки.
опишет окружность единичного радиуса против часовой стрелки.
В отличии от функции  , функция
, функция  периодическая с периодом T = 2 π.
периодическая с периодом T = 2 π.