
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 1: Кинематика. Виды прямолинейного движения.
|
|
Кинематика – это раздел механики, в котором изучают движение тел, не рассматривая причины, влияющие на их движение. Иными словами, кинематика отвечает на вопрос: «как тело движется?».
Параметрами кинематики являются: путь S(м.), перемещение  (м.), время t(с.), скорость
(м.), время t(с.), скорость 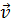 (м/с), ускорение
(м/с), ускорение  .(м/с2).
.(м/с2).
Путь S – это длина траектории тела. Путь – скалярная величина.
Перемещение  – это вектор, соединяющий начальное и конечное положение тела, и направленный к конечному положению.
– это вектор, соединяющий начальное и конечное положение тела, и направленный к конечному положению.
В процессе движения путь может только увеличиваться, а перемещения – и увеличиваться и уменьшаться.
Время t – это количественная мера протяженности процесса. Время – скалярная и всегда положительная величина.
Скорость  – это количественная характеристика быстроты перемещения. Скорость – векторная величина. Направление вектора скорости
– это количественная характеристика быстроты перемещения. Скорость – векторная величина. Направление вектора скорости 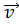 всегда совпадает с направлением вектора перемещения
всегда совпадает с направлением вектора перемещения  .
.
Ускорение 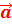 – характеризует быстроту изменения скорости. Ускорение – это векторная величина. Вектор ускорения по модулю совпадает с вектором изменения скорости
– характеризует быстроту изменения скорости. Ускорение – это векторная величина. Вектор ускорения по модулю совпадает с вектором изменения скорости 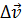 .
.

Замечание: Знак ∆ (дельта) означает разность конечного и начального значения. Т.е. 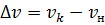
Виды прямолинейного движения:
1. Равномерное движение – это движение с постоянной скоростью 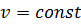 . (Формулы 1-2)
. (Формулы 1-2)
2. Равноускоренное движение – это движение с постоянным ускорением 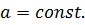 (Формулы 3-10)
(Формулы 3-10)
3. Движение с переменным ускорением (Формулы 11-13)
Равномерное движение (v = const, a = 0).
Формулы для равномерного движения:
 (1.)
(1.)
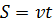 (2.)
(2.)
Здесь: x – конечная координата (м.),  – начальная координата (м.),
– начальная координата (м.), 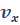 – проекция скорости на ось координат (м/с), t – время (с), S – путь (м),
– проекция скорости на ось координат (м/с), t – время (с), S – путь (м), 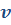 – модуль скорости (м/с).
– модуль скорости (м/с).
На рис.1 представлен график зависимости координаты, на рис. 2 – пути, на рис. 3 – скорости равномерного движения.
На графиках координаты и пути равномерного движения скорость численно равна тангенсу угла наклона графика к оси времени.
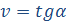
На графике скорости (рис.3) равномерного движения путь численно равен площади прямоугольника, ограниченного самим графиком, осью времени и перпендикулярами, восстановленными из точек, соответствующих начальному и конечному моментам времени.
Равноускоренное движение (a = const)
Формулы для равноускоренного движения:
Здесь: x – конечная координата (м.),  – начальная координата (м.), – начальная координата (м.), 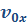 – проекция начальной скорости на ось координат (м/с), – проекция начальной скорости на ось координат (м/с), 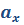 – проекция ускорения на ось координат, t – время движения (с), a - ускорение (м/с2), – проекция ускорения на ось координат, t – время движения (с), a - ускорение (м/с2),  – изменение скорости (м/с), – изменение скорости (м/с), 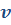 – модуль конечной скорости (м/с), – модуль конечной скорости (м/с), 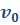 - модуль начальной скорости (м/с), - модуль начальной скорости (м/с), 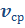 - средняя скорость (м/с), - средняя скорость (м/с),  - весь путь пройденный телом (м.), S – путь(м.), - весь путь пройденный телом (м.), S – путь(м.),  – путь пройденный телом за n-ую секунду (м.), n – номер этой секунды (безразм.). – путь пройденный телом за n-ую секунду (м.), n – номер этой секунды (безразм.).
|
 (3.)
(3.)
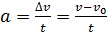 (4.)
(4.)
 (5.)
(5.)
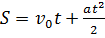 (6.)
(6.)
 (7.)
(7.)
 (8.)
(8.)
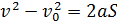 (9.)
(9.)
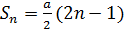 (10.)
(10.)
На рис.4. представлен график координаты, на рис 5. – пути, на рис.6 скорости равноускоренного движения.
Графики координаты и пути равноускоренного движения представляют собой ветви параболы. Та парабола которая ближе к оси координат соответствует большему ускорению. На графиках координаты и пути (рис 4., рис 5.) скорость в точке численно равна тангенсу угла наклона касательной к графику в этой точке.
На графике скорости равноускоренного движения (рис.6) ускорение численно равно тангенсу угла наклона графика к оси времени. Путь же при равноускоренном движении графически можно найти как площадь фигуры ограниченной графиком скорости и перпендикулярами, восстановленными из точек соответствующих начальному и конечному моменту времени.