
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Бит. Системы счисления. Позиционные и непозиционные.
|
|
На практике информация всегда представляется в виде каких-либо сообщений. Информационное сообщение связано с источником информации, приемником информации и каналом передачи. Сообщение от источника к приемнику передается в материально-энергетической форме (электрической, световой, звуковой и т.д.). Человек воспринимает сообщение посредством органов чувств. Технические устройства воспринимают сообщения с помощью специальной аппаратуры – датчиков. Информация может быть непрерывной, или аналоговой, либо дискретной. В некоторых случаях переход от непрерывного представления информационного сигнала к дискретному дает значительные преимущества при передаче, хранении и обработке информации. Для этих целей в информационной технике используются аналого-цифровые преобразователи; обратное преобразование информации осуществляется цифро-аналоговыми преобразователями.
Для представления дискретной информации в цифровых вычислительных машинах применяется алфавитный способ, основой которого является использование фиксированного набора символов любой природы, называемого алфавитом. Символы из набора алфавита называются буквами, а любая конечная последовательность букв – словом в этом алфавите. При этом не требуется, чтобы слово обязательно имело языковое смысловое значение.
Для ввода в ЭВМ информация должна быть перенесена на специальный носитель, с которого она воспринимается машиной. Исходным носителем информации служит бумага. На перфокарты и перфоленты символы наносятся посредством совокупности пробитых и непробитых позиций. На магнитных носителях информации – лентах, дисках, барабанах и картах – для нанесения информации используется чередование участков с различной намагниченностью. Таким образом, для представления информации на указанных носителях используется алфавит, включающий в себя всего две буквы (есть пробивка, нет пробивки; есть намагниченность, нет намагниченности).
Очевидно, что процесс преобразования информации требует представления букв одного алфавита буквами или словами другого алфавита. Такое преобразование называется кодированием. Процесс обратного преобразования информации относительно ранее выполненного кодирования называется декодированием.
В вычислительной технике получило распространение двоичное кодирование информации, при котором вводимые в ЭВМ символы представляются средствами двоичного алфавита, состоящего из двух букв – символов 0 и 1.
Независимо от того, как изображает исходные данные пользователь (числа или строки символов), они преобразуются в последовательности двоичных цифр 0 и 1. При выводе информации осуществляется обратное преобразование двоичных данных в удобную для пользователя форму.
Двоичная цифра называется битом. Группа из n бит позволяет представить 2 n комбинаций от 00...00 до 11...11. Представление данных группой из восьми бит называется байтом. С помощью одного байта можно закодировать 28=256 различных комбинаций. В информатике байт стал стандартной базовой единицей измерения количества информации. Содержание байта может интерпретироваться по-разному: оно может быть кодированным представлением символа внешнего алфавита, целым или вещественным числом, частью машинной команды и т.д. Интерпретацию байта фактически осуществляет программист в зависимости от контекста своей программы.
Биты в байте нумеруются справа налево, начиная с нуля. Четыре соседних бита в байте называются тетрадой. Единица данных, кратная байту и равная разрядности регистров процессора ЭВМ, называется машинным словом. Машинное слово является основной единицей данных, которой оперирует процессор ЭВМ. Длина слова может составлять 1, 2, 4, 8 и более байт.
Для представления больших объемов информации используются производные от байта крупные единицы измерения: килобайт (Кбайт), мегабайт (Мбайт), гигабайт (Гбайт). При этом выполняются следующие соотношения:
1 Кбайт = 210 = 1024 байт;
1 Мбайт = 220 = 1 048 576 байт;
1 Гбайт = 230 = 1 073 741 824 байт.
Процесс обработки информации в ЭВМ сопровождается преобразованием чисел из одной системы счисления в другую.
Система счисления – это совокупность правил наименования и записи чисел. Существуют два вида систем счисления – позиционные и непозиционные.
Непозиционные системы счисления появились значительно раньше позиционных систем. В них символы, обозначающие какое-то число, не меняют своего значения в зависимости от местоположения в изображении этого числа. Самая известная непозиционная система счисления – римская, в которой для записи чисел используются буквы латинского алфавита. Буква I всегда означает единицу, буква V – пять, X – десять, L – пятьдесят, C – сто, D – пятьсот, M – тысячу и т.д. Например, десятичное число 267 записывается в римской системе счисления как CCLXVII.
В информатике применяются только позиционные системы счисления. В каждой позиционной системе счисления используется определенный набор символов, называемых цифрами, последовательная запись которых изображает число. Количество символов в наборе соответствует основанию системы счисления. Позиция символа в изображении числа называется разрядом. Младший разряд целой части числа имеет номер 0. Каждой цифре соответствует число, которое меньше основания системы счисления. В зависимости от позиции цифры в числе ее значение умножается на степень основания, показатель которой равен номеру разряда.
Таким образом, целое положительное число A в позиционной системе счисления можно представить следующим выражением:
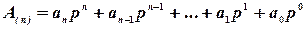 ,
,
где p – основание системы счисления, натуральное число;  – цифра; n – номер старшего разряда числа.
– цифра; n – номер старшего разряда числа.
Показатели степени основания для дробной части числа изображаются отрицательными числами от –1 до 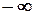 . Смешанное число в общем виде можно представить следующим выражением:
. Смешанное число в общем виде можно представить следующим выражением:
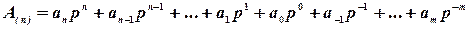 .
.
В современной информатике используются двоичная, восьмеричная, десятичная и шестнадцатеричная системы счисления.
Двоичная система счисления имеет набор цифр {0, 1} и p =2. Двоичное число можно представить таким выражением:
 .
.
Пример. 11012 = 1·23 + 1·22 + 0·21 + 1·20 = 1310.
Восьмеричная система счисления в настоящее время в информатике практически не используется. Она имеет набор цифр {0, 1, 2, 3, 4, 5, 6, 7} и p =8. Представление восьмеричного числа:
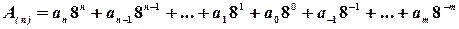 .
.
Пример. 3778 = 3·82 + 7·81 + 7·80 = 25510
Десятичная система счисления используется в нашей повседневной жизни, имеет набор цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} и p =10. Представление десятичного числа:
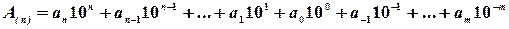 .
.
Пример. 152, 710 = 1·102 + 5·101 + 2·100 + 7·10-1.
Шестнадцатеричная система счисления имеет набор цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F} и p =16. Для изображения первых десяти цифр используются цифры десятичной системы счисления, а для изображения остальных цифр – шесть первых букв латинского алфавита. Представление шестнадцатеричного числа:
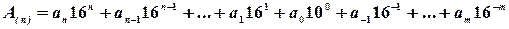 .
.
Пример. E7F816 = E·163 + 7·162 + F·161 + 8·160 = 5938410.
Двоичная система счисления получила исключительное распространение в вычислительной технике благодаря представлению цифры каждого разряда электронной схемой с двумя устойчивыми состояниями и простоте выполнения арифметических операций. Восьмеричная и шестнадцатеричная системы счисления представляет собой более компактную форму записи двоичных чисел, при которой три или четыре двоичные цифры заменяются либо на одну восьмеричную, либо на две шестнадцатеричные.
Поскольку люди и вычислительные машины пользуются различными системами счисления, следует знать принципы перевода чисел из одной системы счисления в другую. Преобразование числа из системы счисления с произвольным основанием в десятичное представление производится по вышеприведенным соотношениям. Далее рассмотрим другие правила перевода целых чисел ручным методом.
Правило 1. Для перевода целого десятичного числа x в систему счисления с основанием p необходимо делить исходное число x и образующиеся частные на p до получения частного, равного нулю. Искомое представление есть последовательность остатков от деления, причем первый остаток есть младшая цифра.
Пример. Перевод десятичного числа 236 в двоичное число:
| Частные | Остатки |
| 0 = а0 0 = а1 1 = a2 1 = a3 0 = a4 1 = a5 1 = a6 1 = a7 |
Записывая остатки от деления снизу вверх, получим: 23610 = 111011002.
Правило 2. Для перевода целого двоичного числа в шестнадцатеричную систему счисления необходимо исходное число справа налево сгруппировать по четыре цифры, а затем каждую группу записать одной шестнадцатеричной цифрой.
Пример. Перевод двоичного числа 1111010 в шестнадцатеричное число:
1111010(2) = 0111 1010 = 7A(16).
Перевод двоичных чисел в восьмеричные осуществляется по правилу 2, но группировать двоичные цифры следует по три.
Правило 3. Для перевода целого шестнадцатеричного числа в двоичное необходимо каждую цифру исходного числа записать в виде эквивалентного четырехбитного двоичного числа.
Пример. Перевод шестнадцатеричного числа 5AF в двоичное число:
5AF(16) = 0101 1010 1111 = 01011010111(2).
Перевод восьмеричного числа в двоичное производится аналогичным образом, но при этом каждая восьмеричная цифра должна быть записана в виде трехбитного двоичного числа.
Для ручного перевода чисел из одной системы счисления в другую можно воспользоваться табл. 4.1.
Таблица 1.1
Таблица перевода чисел
| Десятичное число | Шестнадцатеричное число | Восьмеричное число | Двоичное число |
| A B C D E F |