Лекция 5. Принцип д’Аламбера-Лагранжа. Обобщенные силы. Общее уравнение динамики в обобщенных координатах.

Легко показать, что все типы связей, обычно рассматриваемые в задачах механики – гладкая поверхность, идеальная нить, шарниры, подпятник, глухая заделка ‑ являются идеальными. Неидеальность связей часто обусловлена наличием трения скольжения или качения. В этом случае часть реакции связи, для которой нарушается идеальность, переводится формально в разряд активных сил и задается в условии или определяется в задаче. В дальнейшем мы будем рассматривать именно такие механические системы, то есть системы с идеальными связями или со связями, которые описанным приемом могут быть переведены в разряд идеальных. Для таких систем имеет смысл сформулировать положение, которое также имеет форму аксиомы, объединяющее II закон Ньютона, принцип независимости действия сил (точнее правило параллелограмма), принцип освобождаемости от связей и принцип идеальности связей. Это положение называется в литературе по механике по-разному – принцип д’Аламбера-Лагранжа, общее вариационное уравнение механики, общее уравнение динамики и др. Применение этого принципа для вывода других положений и теорем теоретической механики дает существенный выигрыш, и будет использоваться нами постоянно.

Каждая точка механической системы может взаимодействовать с другими точками и телами данной механической системы, с точками и телами, не принадлежащими ей, а также с внутренними и внешними связями. Объединим все силы реакций указанных связей, действующих на i -ю точку МС, в одну силу 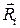, согласно правилу параллелограмма складывая их попарно. То же самое сделаем с активными силами, получим силу . С помощью 2-го закона Ньютона запишем уравнения движения точек системы

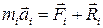, i=1, 2, …, N. (5.1)

Чтобы применить условие идеальности связей, надо разрешить эти уравнения относительно реакций связей 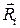и подставить полученные выражения в (4.8). Это дает

.

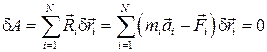Для более удобной формулировки этого принципа поменяем местами слагаемые в круглых скобках. Величину

,

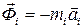имеющую размерность силы, в механике принято называть Д’Аламберова сила инерции точки или просто сила инерции точки. Тогда

в каждый момент времени при движении механической системы с идеальными удерживающими связями сумма виртуальных работ активных сил и сил инерции равна нулю

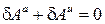или (5.2)

Обобщенные силы. Пусть имеется явно или неявно заданное выражение радиус-векторов точек системы через обобщенные координаты и время t

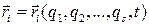, i =1, 2, …, N. (5.3)

Применим операцию изохронного варьирования к выражению (7.1), заключающуюся в том, что надо взять дифференциал от функции нескольких переменных , полагая время фиксированным. Получим

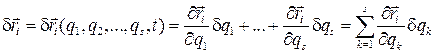. (5.4)

Подставим это выражение в формулу виртуальной работы i -ой активной силы и просуммируем эти работы по всем точкам системы. Получим

.

Перегруппируем слагаемые в этом выражении и изменим порядок суммирования, получим

. (5.5)

Здесь 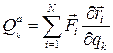, k=1, 2, …, s (5.6)

и есть обобщенная сила, соответствующая обобщенной координате с номером k. Таким образом, обобщенную силу можно определить как

коэффициент, стоящий перед вариацией обобщенной координаты в выражении виртуальной работы системы.

Из выражений (5.5) и (5.6) можно получить два способа вычисления обобщенных сил. Один — прямо по определению, второй – по формуле (5.6), если заданы проекции сил и аналитические зависимости координат их точек приложения от обобщенных (5.4). В дальнейшем мы рассмотрим подробнее способы вычисления обобщенных сил. Для ближайших целей нам достаточно выражения (5.6) и данного определения. Подчеркнем, что обобщенная сила, в отличие от обычной, является скалярной величиной и называется так только потому, что выражение (5.3) по форме напоминает выражение виртуальной работы силы

.

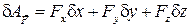Из правой части этой формулы видно, что имело бы смысл говорить об обобщенных силах как проекциях сил системы на обобщенные координаты.

Совершенно аналогично, можно записать выражение для обобщенной силы инерции, подставив в (7.4) вместо активной силы силу инерции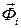

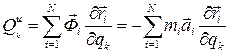, k=1, 2, …, s. (5.7)

Общее уравнение механики в обобщенных координатах. На основании (5.5) запишем выражение виртуальных работ активных сил и сил инерции механической системы и приравняем его нулю согласно (5.2)

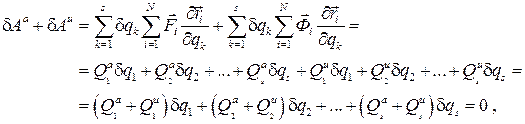
откуда, благодаря независимости вариаций обобщенных координат 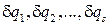друг от друга, что имеет место для голономных систем, следует s уравнений

.

или в другой форме, напоминающей II закон Ньютона (3.10)

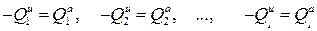(5.8)

Эти уравнения и являются уравнениями, описывающими динамическое поведение механической системы с голономными связями. Их можно применять непосредственно для вывода уравнений движения. Основная трудность здесь состоит в получении выражений приведенных сил инерции, которые можно определить по формулам (5.7). В дальнейшем будет показано, как можно построить алгоритмы компьютерной алгебры для автоматизации построения уравнений движения достаточно широкого класса механических систем на базе уравнений (5.6)-(5.8). Однако для «ручного» вывода уравнений движения более предпочтительным оказывается применение уравнений Лагранжа II рода, которые получаются из (5.8) выражением обобщенных сил инерции (5.7) через кинетическую энергию системы.