Связанная система координат

Представляет собой декартовую прямоугольную правую систему осей координат, неподвижную относительно ракеты или ГЧ. Оси этой системы называют связанными осями.

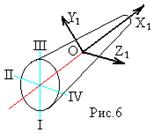Начало связанной системы координат помещено в центр тяжести (или в центр масс) ракеты. Ось Ox₁ направлена по продольной оси ракеты в сторону ГЧ. Ось Oy₁ расположена в плоскости симметрии ракеты, которая в момент старта совпадает с плоскостью стрельбы (плоскостью x_cOy_c) стартовой системы координат. Ось Oy₁ направлена в сторону третьего стабилизатора, ось Oz₁ направлена – в сторону четвертого. Для ГЧ направление осей Oy₁ и Oz₁ удобно выбрать такими, чтобы ГЧ состыкованной с ракетой ось Oy₁ была направдена в сторону третьего стабилизатора, а ось Oz₁ – в сторону четвертого.

При установке ракеты на стартовый стол плоскость стабилизаторов I и III совпадает с плоскостью стрельбы, а стабилизатор I направлен в сторону цели.

Связанная система координат иногда называется “подвижная” система координат.

3) Скоростная система координат (поточная)

Декартовая, прямоугольная, правая.

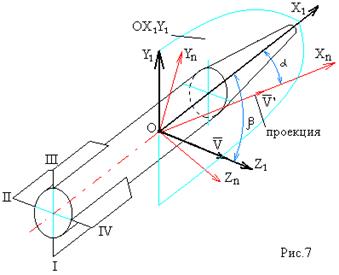
Начало системы (точка О) расположено в центре тяжести ракеты. Ось Ox_n направлена по вектору скорости ракеты 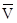. Ось Oy_n перпендикулярна Ox_n и лежит в плоскости симметрии ракеты Ox₁y₁.

Ориентация ракеты относительно вектора скорости 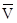в общем случае определяется двумя углами:

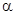- угол атаки;

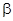- угол скольжения.

Угол 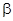- это угол между вектором скорости 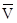и плоскостью ракеты Ox₁y_1.

Угол 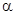- это угол между проекцией вектора скорости 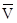на плоскость симметрии ракеты Ox₁y₁ и продольной осью ракеты Ox₁.