Логические выражения (составные высказывания).

Логические операции имеют следующий приоритет: действия в скобках, инверсия, &, v, , ~.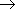

Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания.

Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности.

Алгоритм построения таблицы истинности:

1. подсчитать количество переменных n в логическом выражении;

2. определить число строк в таблице m = 2 ⁿ;

3. подсчитать количество логических операций в формуле;

4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;

5. определить количество столбцов в таблице: число переменных плюс число операций;

6. выписать наборы входных переменных с учетом того, что они представляют собой натуральный ряд n-разрядных двоичных чисел от 0 до 2 ⁿ -1;

7. провести заполнение таблицы истинности по столбикам, выполняя логические операции в соответствии с установленной в п.4 последовательностью.

Наборы входных переменных, во избежание ошибок, рекомендуют перечислять следующим образом:

а) определить количество наборов входных переменных;

б) разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки 0, а нижнюю -1;

в) разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами 0 или 1, начиная с группы 0;

г) продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами 0 или 1 до тех пор, пока группы 0 и 1 не будут состоять из одного символа.

Пример. Для формулы A& (B v C) построить таблицу истинности алгебраически и с использованием электронных таблиц.

Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 2³ = 8.

Количество логических операций в формуле 2, следовательно, количество столбцов в таблице истинности должно быть 2+3 = 5.

Логические выражения называются равносильными, если их истинностные значения совпадают при любых значениях, входящих в них логических переменных.

Аппарат алгебры логики можно с успехом использовать для решения содержательных задач. Однако для этого необходимо научиться правильно переводить высказывания с естественного языка на символический язык алгебры логики.

Рассмотрим пример. Перевести на язык алгебры высказываний следующее предложение: