
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Скалярное произведение векторов
|
|
Важной нелинейной операцией над векторами является скалярное произведение векторов.
Определение 3. Скалярным произведением геометрических векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Это определение можно записать в виде формулы  . Здесь
. Здесь 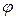 - угол между векторами
- угол между векторами 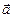 и
и  ,
,  ,
, 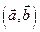 - обозначения для скалярного произведения.
- обозначения для скалярного произведения.
Справедливы следующие свойства скалярного произведения:
1) 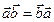
2) 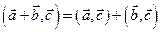
3) 
4)  ,
, 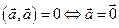 .
.
Свойства 1) и 4) прямо следуют из определения скалярного произведения. Для доказательства свойств 2) и 3) удобно воспользоваться понятием проекции вектора на вектор (или на направление, им порождаемое).
Определение 4. Проекцией вектора 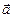 на вектор
на вектор  (или на направление, порождаемое вектором
(или на направление, порождаемое вектором  ) называется число, равное произведению длины вектора на косинус угла
) называется число, равное произведению длины вектора на косинус угла 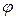 между вектором
между вектором 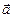 и направлением, порождаемым вектором
и направлением, порождаемым вектором  .
.
Итак, по определению 4 справедлива формула 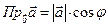 . При этом для скалярного произведения справедлива формула
. При этом для скалярного произведения справедлива формула 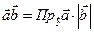 .
.
Теорема 3. Проекция линейной комбинации векторов 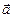 и
и  на вектор
на вектор  равна линейной комбинации проекций векторов
равна линейной комбинации проекций векторов 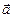 и
и  на вектор
на вектор  .
.
Доказательство. Теорема 3 утверждает, что справедлива формула  . Для доказательства достаточно заметить, что при умножении вектора на число его проекция умножается на это число, т. е. справедлива формула
. Для доказательства достаточно заметить, что при умножении вектора на число его проекция умножается на это число, т. е. справедлива формула  . Кроме того, несложно проверить, что проекция суммы векторов равна сумме их проекций, т. е. справедлива формула
. Кроме того, несложно проверить, что проекция суммы векторов равна сумме их проекций, т. е. справедлива формула 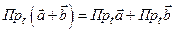 . Теорема доказана.
. Теорема доказана.
Для проверки свойств 2 и 3 скалярного произведения заметим, что:
 ,
,
 .
.
_. Вычисление скалярного произведения
в декартовой системе координат