
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 1.1.
|
|
Алгоритм сложения двух чисел(a и b).
1. Спросить, чему равно число a.
2. Спросить, чему равно число b.
3. Сложить a и b, результат присвоить с.
4. Сообщить результат с.
Достоинством данного способа является простота описания, а к недостаткам можно отнести то, что такой подход многословен и не имеет строгой формализации, поэтому допускает неоднозначность толкования отдельных предписаний, в силу чего словесный способ представления алгоритма не имеет широкого распространения.
Для строгого задания различных структур данных и алгоритмов их обработки требуется иметь такую систему формальных обозначений и правил, чтобы смысл всякого используемого предписания трактовался точно и однозначно. Соответствующие системы правил называются языками описаний. К ним относятся алгоритмические языки (псевдокоды), блок-схемы и языки программирования.
Структурно-стилизованный способ описания алгоритма основан на записи алгоритмов в формализованном представлении предписаний, задаваемых путем использования ограниченного набора типовых синтаксических конструкций, называемых часто псевдокодами.
Достоинством псевдокодов является близость к языкам программирования, а недостатками, в свою очередь, являются сложность освоения и невозможность непосредственного ввода алгоритма для решения на ЭВМ, т.е. необходимость перевода на язык программирования.
Графический способ описания алгоритма предполагает, что для описания структуры алгоритма используется совокупность графических изображений (блоков), соединяемых линиями передачи управления. Такое изображение называется методом блок-схем.
Блок-схема алгоритма – это графическое представление хода решения задачи. Блок-схема состоит из блоков, соединенных линиями, а блоки изображаются в виде геометрических фигур, называемых символами. Внутри символов записываются указания о выполняемых блоком функциях – формулы, текст, логические выражения. Вид символов и правила выполнения блок-схем стандартизированы – ГОСТ 19.701-90 содержит перечень символов, их наименования, отображаемые функции, формы и размеры, а также правила выполнения схем. При разработке алгоритма каждое действие обозначают соответствующим блоком, показывая их последовательность линиями со стрелками на конце. Названия, обозначения и назначение элементов блок-схем приводится на рис. 1.1.
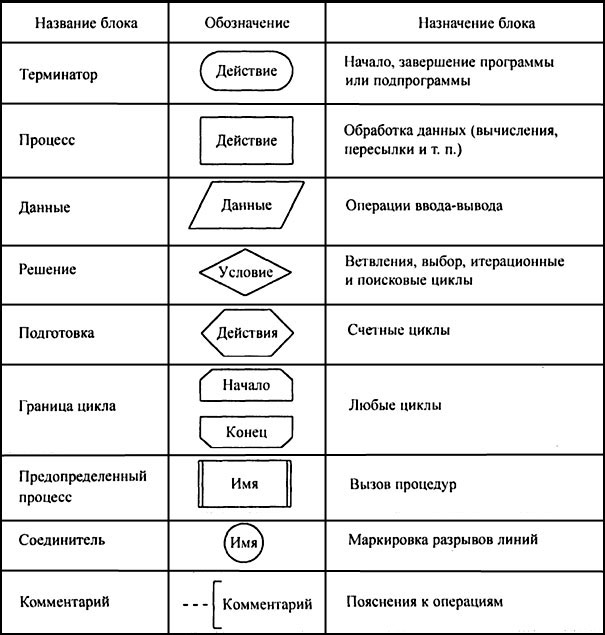
Рисунок 1.1 – Основные блоки
Следует упомянуть некоторые основные правила выполнения блок-схем, которыми надлежит руководствоваться при графическом описании алгоритмов. Начало алгоритмов отмечается символом " Терминатор", из которого выходит одна линия. В нем записывается слово " Пуск" (" Начало"). Конец алгоритма отмечается этим же символом, в котором записывается слово " Останов" (" Конец"). В этом случае данный символ не имеет ни одной выходной линии, а на него может замыкаться одна или более линий. Символ “Процесс” может иметь одну или несколько входных линий и только одну выходную. Внутри символа может быть записано несколько предписаний – в этом случае они выполняются в порядке записи. Представление отдельных операций достаточно свободно. Для обозначения вычислений можно использовать математические выражения, для пересылки данных – стрелки, для других действий – пояснения на естественном языке, например, А: = Х + 4; i: = i + 1, < A > ––> B.
Линии потока должны быть параллельны сторонам листа. Основные направления линий потока – сверху вниз и слева направо – стрелкой не обозначаются. В других случаях на конце линии потока ставится стрелка, а в месте слияния линий ставится точка. Если блок-схема не умещается на одном листе, используют соединители. При переходе на другой лист или получении управления с другого листа в комментарии указывается номер листа, например " с листа 3" " на лист 1".
Для записи алгоритма любой сложности достаточно трех базовых структур:
1) следование - обозначает последовательное выполнение действий (рис. 1.2, а);
2) ветвление - соответствует выбору одного из двух вариантов действий (рис. 1.2, б);
3) цикл-пока - определяет повторение действий, пока не будет нарушено условие, выполнение которого проверяется в начале цикла (рис. 1.2, в).

Рисунок 1.2 – Базовые алгоритмические структуры
Кроме этого, при описании алгоритмов используются дополнительные алгоритмические структуры, производные от базовых, каждая из которых может быть реализована через базовые структуры:
1) выбор - выбор одного варианта из нескольких в зависимости от значения некоторой величины (рис. 1.3, а, б);
2) цикл-до - повторение некоторых действий до выполнения заданного условия, проверка которого осуществляется после выполнения действий в цикле (рис. 1.3, в, г);
3) цикл с заданным числом повторений (счетный цикл) – повторение некоторых действий указанное число раз (рис. 1.3, д, е).

Рисунок 1.3 – Реализация дополнительных алгоритмических структур
через базовые структуры
Рассмотрим примеры графического описания алгоритмов различных типов: линейного, разветвляющегося, циклического и комбинированного (рис. 1.4 – 1.7).
Пример 1.2. Линейный алгоритм.
Алгоритм вычисления значения выражения K=3b+6а (рис. 1.4).
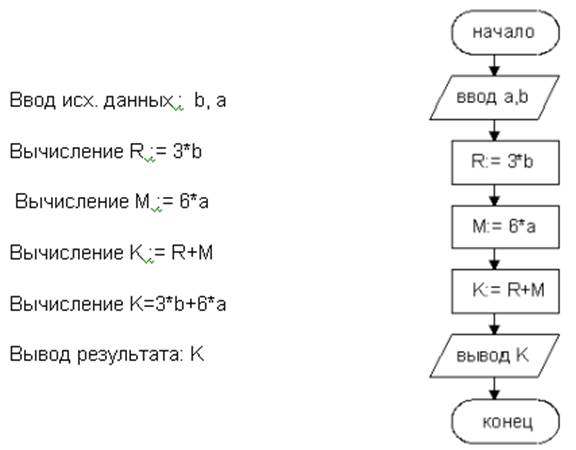
Рисунок 1.4 – Пример блок-схемы линейного алгоритма
Пример 1.3. Разветвляющийся алгоритм.
Алгоритм, определяющий, пройдет ли график функции y=3x+4 через точку с координатами x1, y1 (рис. 1.5).
 |
Рисунок 1.5 – Пример блок-схемы разветвляющегося алгоритма
Пример 1.4. Циклический алгоритм.
Алгоритм, определяющий факториал натурального числа n (рис. 1.6):
n! = 1*2*3*….*(n-1)*n
0! =1
5! =1*2*3*4*5=120
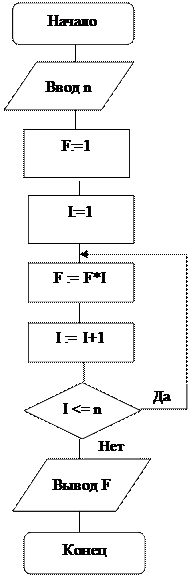 |
Рисунок 1.6 – Пример блок-схемы циклического алгоритма
Пример 1.5. Комбинированный алгоритм.
Необходимо определить наибольший общий делитель двух натуральных чисел А и В.
Для решения поставленной задачи используем алгоритм Евклида, который заключается в последовательной замене большего из чисел на разность большего и меньшего, пока числа не станут равны. Рассмотрим данный алгоритм на двух примерах.
Пример (а): А=225, В=125. Применяя алгоритм Евклида, получаем для А и В наибольший общий делитель, равный 25.
Пример (б): А=13, В=4. В этом случае наибольший общий делитель А и В равен 1.
| a) | A | B | |||||||
| 225-125=100 | |||||||||
| 25-100=25 | |||||||||
| 100-25=75 | |||||||||
| 75-25=50 | |||||||||
| 50-25=25 | =25 | ||||||||
| б) | A | B | |||||||
| 13-4=9 | |||||||||
| 9-4=5 | |||||||||
| 5-4=1 | |||||||||
| 4-1=3 | |||||||||
| 3-1=2 | |||||||||
| =1 | 2-1=1 | ||||||||
Блок-схема алгоритма Евклида для нахождения наибольшего общего делителя двух натуральных чисел показана на рис. 1.7.
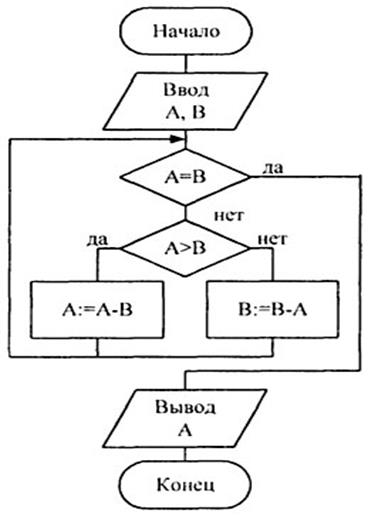
Рисунок 1.7 – Пример блок-схемы комбинированного алгоритма
Блок-схема алгоритма детально отображает все особенности разработанного алгоритма, но иногда такой высокий уровень детализации не позволяет выделить суть алгоритма. В этих случаях для описания алгоритма используют псевдокод. Псевдокод базируется на тех же основных структурах, что и структурные схемы алгоритма (табл. 1.1).
Пример 1.6. Описание алгоритма Евклида на псевдокоде.
Алгоритм Евклида:
Ввести А, В
цикл-пока А ≠ В
если А > В
то А: = А - В
иначе В: = В - А