
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Формы представления алгоритмов
|
|
Глава 3.ОСНОВЫ АЛГОРИТМИЗАЦИИ И ПРОГРАММИРОВАНИЯ
Понятие алгоритма и его свойства
Понятие алгоритма является одним из фундаментальных понятий информатики и является объектом исследования ее специального раздела - основ алгоритмизации. Слово " алгоритм" в сущности является синонимом слов способ, рецепт, порядок и т.д. Можно говорить в этом смысле об алгоритме нахождения корней квадратного уравнения, заданного своими коэффициентами, или об алгоритме разложения натурального числа на простые множители. В основе этих алгоритмов лежат простейшие математические операции над числами. Такие алгоритмы называются численными или математическими.
Довольно часто рассматриваются и нечисленные алгоритмы, где объектами операций являются не числа. В роли данных могут выступать последовательности символов - тексты, формулы и т.д.; в роли операций - не операции сложения, умножения и подобные им, а операции приписывания одной последовательности к другой, операции замены по некоторой таблице одних символов на другие и т.д. Примером алгоритма, основывающегося на подобных операциях, являются алгоритмы преобразования текста в код Морзе.
Алгоритм - это некоторая конечная последовательность точных предписаний (правил), однозначно определяющая процесс преобразования исходных и промежуточных данных в конечный результат при решении множества задач данного типа.
Поиски различных алгоритмов входили в круг важных задач во все время существования науки. В качестве примера рассмотрим алгоритм Евклида (III век до н.э.), решающий все задачи следующего типа: для двух натуральных чисел Х и Y найти их наибольший общий делитель (НОД). Суть задачи заключается в последовательности деления чисел. Заменив деление повторным вычитанием, получим одну из формулировок этого алгоритма:
1. Присвоить переменным X и Y исходные значения.
2. Если X > Y, то перейти к п. 4, иначе к п. 3.
3. Если X < Y, то перейти к п. 5, иначе к п. 6.
4. Заменить пару (X, Y) парой (X-Y, Y) и вернуться к п. 2.
5. Заменить пару (X, Y) парой (X, Y-X) и вернуться к п. 2.
6. Здесь Х=Y. Считать НОД равным Х или Y.
7. Конец работы.
Составим таблицу, показывающую, как с течением времени после выполнения очередного шага меняются значения X и Y. В качестве исходного данного возьмем пару чисел (100, 80).
Работа алгоритма Евклида может быть изображена в виде таблицы (табл.3.1).
Алгоритм Евклида Табл. 3.1.
| Момент времени | Шаг Алгоритма | X | Y | ? (X> Y) | ? (X< Y) |
| ДА НЕТ НЕТ НЕТ НЕТ | ДА ДА ДА НЕТ | ||||
| НОД=20 | |||||
| КОНЕЦ РАБОТЫ |
В настоящее время интерес к алгоритмам особенно велик благодаря упомянутой возможности использования компьютеров в технике, экономике, научных исследованиях и т.д. Дело здесь в том, что компьютер во время работы выполняет заданную программу, а программа является некоторым алгоритмом, записанным в специальных обозначениях. Соответствующую систему обозначений называют языком программирования. Точнее, язык программирования - это совокупность средств и правил представления алгоритма в виде, приемлемом для компьютера. Число используемых языков программирования сейчас достаточно велико. Среди наиболее распространенных следует в первую очередь назвать такие языки, как Фортран, Алгол, Бейсик, Лисп, Паскаль, Модула, Си, Ада.
Методы разработки программ решения задач - не есть программирование в чистом виде, хотя программирование и является важной составной частью этой дисциплины. Существенную роль в эффективном применении ЭВМ играет алгоритмизация - математическая формализация задач и синтез алгоритмов их численного решения.
В качестве математической основы при формализации и решении прикладных задач рассматриваются широко распространенные методы численного анализа, исследования операций и математического программирования, позволяющие с высокой точностью и эффективностью добиться получения требуемых результатов решения.
Алгоритм - это сформулированное на некотором языке правило, указывающее на действия, последовательное выполнение которых приводит от исходных данных к искомому результату. Значение слова алгоритм очень схоже со значением слов рецепт, процесс, метод, способ. Однако любой алгоритм, в отличие от рецепта или способа, обязательно обладает следующими свойствами..
Дискретность - заключается в том, что процесс решения задачи подразделяется на элементарные предписания или этапы (шаги). Запись алгоритма представляет собой упорядоченную совокупность предписаний, образующих дискретную структуру алгоритма. Предписания при этом выполняются в последовательном порядке.
Детерминированность или определенность - означает однозначность толкования каждого предписания алгоритма. Его многократное выполнение при одних и тех же исходных данных должно приводить к одному и тому же результату.
Результативность - заключается в возможности получения конечного результата для допустимых исходных данных за конечное число шагов.
Массовость, или универсальность, означает возможность его решать серию однотипных задач при различных начальных условиях.
Эффективность - заключается в минимальных затратах времени и трудоемкости для его реализации, использовании меньшего объема оперативной памяти и в минимальных затратах машинного времени на решение задачи.
Формы представления алгоритмов
Алгоритмы имеют несколько форм представления: словесную, формульно-словесную, табличную, в виде блок-схем.
Словесная форма является самой простой и доступной. Содержание последовательных предписаний - вычислений задается в произвольной краткой форме на естественном языке, не допускающем повторений, неоднозначного понимания выражений, лишних слов. Недостаток словесной формы - отсутствие более или менее строгой формализации и наглядности вычислительного процесса. Она не подходит для задач со сложной логикой и вычислительным процессом и применима для простых алгоритмов, отличающихся однократной последовательностью выполнения предписаний.
Пример: Записать алгоритм вычисления y по формуле:
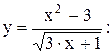
1) умножить x на3;
2) к результату первого действия прибавить 1;
3) из результата второго действия извлечь корень;
4) умножить x на x;
5) из результата четвертого действия вычесть 3;
6) результат пятого действия разделить на результат третьего. Полученный результат считать значением y.
Формульно-словесный способ основан на задании предписания алгоритма с использованием математических формул и словесных пояснений. Формулы в сочетании с правилами их написания представляют собой алгоритмический язык, применимый для задания вычислительных алгоритмов. Этот способ более нагляден и компактен по сравнению со словесным. Однако формула устанавливает последовательность действий неоднозначно, т.е. не совсем полно отражаются свойства детерминированности и определенности.
Пример: Выражение
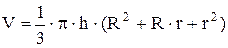
задает объем усеченного конуса. Здесь h-высота, R и r - соответственно радиусы нижнего и верхнего основания.
Табличная форма записи. Существует несколько типов таблиц. Первый используется при организации вычислений по формуле с пооперационной регистрацией промежуточных результатов. Разбиение формулы на последовательность элементарных действий дает последовательность предписаний. Такая форма наиболее применима тогда, когда требуется вычислить несколько значений одного выражения для различных значений входных величин.
Пример: Для предыдущей формулы составим табличную запись алгоритма (рис. 3.1)
| R | r | H | p× h | 1/3× p× h | R2 | R× r | r2 | R2+R× r+r2 | V |
| L | L | L | L | L | L | L | L | L | L |
Рис.3.1. Табличная запись алгоритма
Второй тип таблицы называется решающей таблицей. В простейшем случае она включает 4 части: перечень условий, указатель условий, перечень действий, указатель действий (рис.3.2).
Перечень условий содержит все условия, а перечень действий - все действия, проверка и выполнение которых необходимы в процессе решения задачи. Они располагаются одно за другим; в строке записывается только одно условие или действие. Правая часть делится на несколько столбцов, в которых определяется, какие условия следует проверить, а какие действия следует выполнить в результате проверки этих условий. На пересечении соответствующих столбцов и строк ставится Y в том случае, если условие должно выполняться, N - если нет и " -", если условие не учитывается.
| Номер таблицы | L | k | |||||
| Перечень ì условий í î | Условие 1 | Y | N | Y | L | N | ü Указатель ý условий þ |
| Условие 2 | - | Y | Y | L | N | ||
| L | L | L | L | L | L | ||
| Условие m | Y | - | Y | L | - | ||
| Перечень ì действий í î | Действие 1 | X | X | L | ü Указатель ý действий þ | ||
| Действие 2 | X | L | X | ||||
| L | L | L | L | L | L | ||
| Действие n | X | X | L | X |
Рис.3.2. Общий вид решающей таблицы
Когда условие требует выполнения некоторого действия, то на пересечении соответствующих столбцов и строк, ставится символ X. В случае отсутствия действия позиция остается незаполненной.
Если условие формируется так, что возможны два ответа, " да" - " нет" или " Y" - " N", то таблицы называются таблицами с ограниченными входами. Если ответов несколько, то таблицы называются таблицами с расширенными входами. При этом простое условие записывается так же, как и в таблицах первого вида, сложные действия распределяются между столбцами.
Пример: Алгоритм поиска HOD в виде решающей таблицы с расширенными входами показан в таблице 3.2.
Таблица 3.2.
| Таблица № 0001 | |||
| Условие проверки | a > b | a < b | а = b |
| a = a – b | X | ||
| b = b – a | X | ||
| Перейти к началу | X | X | |
| НОД = а (или b) | X | ||
| Конец | X |
Блок-схемой называется графическое изображение алгоритма, дополненное элементами словесной записи, в котором каждое предписание алгоритма представляется в виде геометрического символа, имеющего определенную конфигурацию в зависимости от характера выполняемой операций или отображаемой функций.
Для однозначного обозначения одинаковых процедур формы, размеры и правила оформления определены ГОСТ 19.003-80 «Схема алгоритмов и программ. Обозначения условные и графические» и ГОСТ 19.002-80 «Схема алгоритмов и программ. Правила оформления».
Наиболее употребительные символы приведены в табл. 3.3.
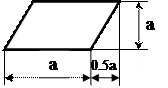
При начертании символов их размеры выбираются кратными 5, размер (а) равным 10, 15, 20.... размер (b) составляет b=1, 5a.
Табл. 3.3
| № п/п | Название Символа | Обозначения и размеры | Отображаемые Функции |

| Процесс | Выполнение действий или последовательности действий | |

| Решение | Выбор направления выполнения алгоритма в зависимости от некоторого условия | |
| Модификация (подготовка) | Выполнение операций, меняющих команды или группы команд. Начало цикла | ||
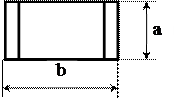
| Типовой процесс | Вычисления по подпрограмме, стандартной программы | |
 5-6
5-6
| Данные | Ввод исходных данных или вывод результатов | |
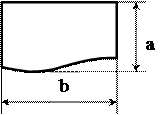
| Документ | Вывод, печать результатов на бумаге | |

| Перфокарта | Ввод и вывод данных, носителем которых являются перфокарты | |
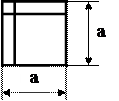
| Процессор (оперативная память) | Операция по преобразованию информации | |

| Магнитный диск | Ввод вывод данных, носителем которых является магнитный диск | |
 11 11
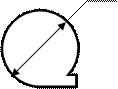
| Магнитная лента | Æ a | Ввод вывод данных, носителем которых является магнитный ленте |
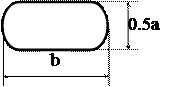 12 12
| Пуск - остановка (знак завершения) | Начало, конец, алгоритма, вход и выход в подпрограмму | |
 12 12
| Линии потока | Указание последовательности связей между символами | |

| Соединитель | Указание связей между прерванными линиями | |
 14 14
| Межстраничный соединитель | Указание связей между элементами схемы, расположенными на разных местах |
Последовательность выполнения пунктов алгоритма, описываемого блок-схемой, устанавливается путем упорядоченного размещения блоков на схеме и объединение их линиями потока. Нормальное направление линии потока - сверху вниз и слева направо. Линии проводятся строго вертикально и горизонтально и завершаются на середине символа. Если направление потока совпадает с нормальным - стрелки не ставятся, если в противоположном направлении - стрелки ставятся. В месте слияния линии потока ставится точка. В месте пересечения линии потока точка не ставится (рис.3.3).
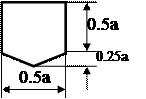
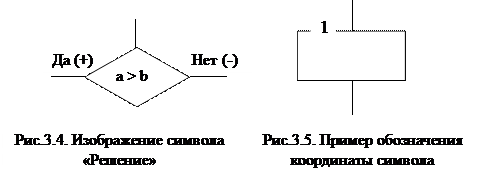
 Выходы символа " Решение" помечаются символами " да" /" нет" - т.е. выполняется или не выполняется условие. Условие записывается внутри символа (рис.3.4). Содержание надписи внутри символа или рядом должно быть кратким, без сокращений, за исключением допустимых сокращений. Записи представляются так, чтобы их можно было читать слева направо, сверху вниз.
Выходы символа " Решение" помечаются символами " да" /" нет" - т.е. выполняется или не выполняется условие. Условие записывается внутри символа (рис.3.4). Содержание надписи внутри символа или рядом должно быть кратким, без сокращений, за исключением допустимых сокращений. Записи представляются так, чтобы их можно было читать слева направо, сверху вниз.
Для удобства нахождения символа задаются их координаты в виде цифр, букв или цифр и букв. Они представляются сверху слева в разрыве контура (рис.3.5).
 Блок-схема является исключительно наглядным и простым способом представления алгоритма. При этом нет никаких ограничений степени детализации в его изображении. Если блок-схема получается очень сложной и теряет свойства иллюстративности, вначале составляют укрупненную блок-схему всего вычислительного процесса, затем каждый ее блок представляется отдельной блок-схемой.
Блок-схема является исключительно наглядным и простым способом представления алгоритма. При этом нет никаких ограничений степени детализации в его изображении. Если блок-схема получается очень сложной и теряет свойства иллюстративности, вначале составляют укрупненную блок-схему всего вычислительного процесса, затем каждый ее блок представляется отдельной блок-схемой.
Для блок-схем обязательны следующие правила: каждый блок имеет только один вход и выполнение описанных в них действий всегда начинается с первого; входить в середину блок-схемы нельзя. Вход в блок-схему обозначается символом " начало", заканчивается блок-схема символом " конец".
Соединители в разрыве линии обозначаются общим идентификатором, в качестве которого может использоваться цифра, буква или буква и цифра (рис.3.6).
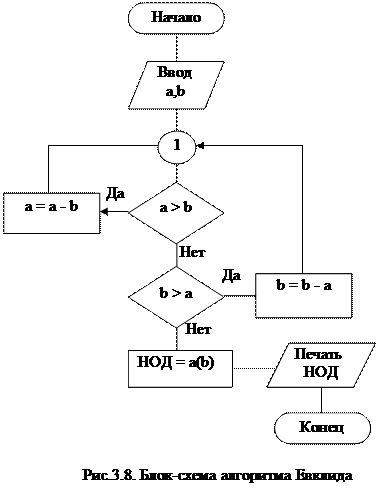 Межстраничный соединитель маркируется двумя строками символов: первая строка определяет лист, вторая является идентификатором самого соединения (рис.3.7).
Межстраничный соединитель маркируется двумя строками символов: первая строка определяет лист, вторая является идентификатором самого соединения (рис.3.7).
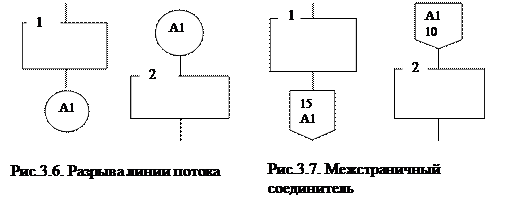
В качестве примера рассмотрим блок-схему алгоритма Евклида нахождения НОД двух чисел (рис.3.8).
 Существует операторная схема записи алгоритма. При операторном способе записи алгоритма каждое предписание (процедура) обозначается определенным символом-оператором. Операторы записываются построчно в порядке их выполнения. В зависимости от своего назначения операторы делятся на действующие, логические и варьирующие.
Существует операторная схема записи алгоритма. При операторном способе записи алгоритма каждое предписание (процедура) обозначается определенным символом-оператором. Операторы записываются построчно в порядке их выполнения. В зависимости от своего назначения операторы делятся на действующие, логические и варьирующие.
Действующие осуществляют непосредственно вычислительные и другие преобразующие операции над информацией.
Логические описывают условия, от которых зависит направление решения.
Варьирующие предусматривают изменение вспомогательных величин, называемых параметрами. Обычно параметры являются либо номерами изменяемых объектов, носящих одинаковые номера (массивы), либо номерами операторов, по какой-то причине объединенных в одну группу.
Полная последовательность операторов, задающая весь процесс решения, называется схемой решения. Операторы на схеме обычно обозначаются условными (стандартными) символами. Наиболее употребительными являются следующие:
Nо - начало процесса;
В - ввод исходных данных;
D(A) - действующий (арифметический);
Р - логический;
V - варьирующий;
W - оператор печати (вывода);
E - оператор останова.
Знаки переходов имеют вид полускобок с числовыми индексами. Левыми полускобками ë 3 é 5 указывается передача управления. Правая нижняя полускобка указывает прием управления 3û 5û , она может соответствовать как верхнему, так и нижнему знакам передачи управления Соответствие определяется равенством числовых индексов После логического оператора могут стоять верхняя и нижняя полускобка передачи управления. Верхняя полускобка соответствует " да ", т.е. выполнению условия. Нижняя полускобка соответствует невыполнению условия, т.е. " нет " Р (а > б) ë 3 é 5.
Операторы получают номера индексов согласно порядка их действия. Если оператор зависит от параметров, например i, j, то он обозначается так 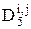 и т.д. Условие записывается в виде функции, где в скобках указывается соответсвующее условие. Варьирующие изменяют параметры V (i, j). Операторная схема алгоритма Евклида имеет вид:
и т.д. Условие записывается в виде функции, где в скобках указывается соответсвующее условие. Варьирующие изменяют параметры V (i, j). Операторная схема алгоритма Евклида имеет вид:
N0 B1 (a, b) 1û P1(а> b)é 2 P2(b> a) é 3ë 4 2û D1(а=a-b) ë 1 3û
D2 (b=b-a)ë 1 4û D3(НОД=а(b))W1 E1.