Численное решение системы дифференциальных уравнений (колебание с одной степенью свободы)

Численное решение системы дифференциальных уравнений

(колебание с одной степенью свободы)

Выполнил: студент I-36 Утин С.В.

Проверил: Огурцов А.В.

Иваново 2011

Численное решение системы дифференциальных уравнений (колебание с одной степенью свободы)

Цель работы.

Изучение численных методов решения дифференциальных уравнений второго порядка и систем дифференциальных уравнений первого порядка.

Задание.

Численно и аналитически найти закон движения материальной точки на пружинке х(t) для заданных режимов. Построить графики искомых функций.

Вариант №1:

Движения материальной точки на пружинке при режимах:

1) свободные незатухающие колебания

2) затухающее колебательное движение

3) вынужденное колебание без сопротивления

Теоретическое введение:

Дифференциальным уравнением второго порядка называется уравнение вида

F(x, y, у', y")=0 (1) или y" =f(x, y, y'). (2)

Функция y(x), при подстановке которой уравнение обращается в тождество, называется решением дифференциального уравнения.

При численном решении ищется частное решение уравнения (2), которое удовлетворяет заданным начальным условиям, то есть решается задача Коши.

Для численного решения дифференциальное уравнение второго порядка преобразуется в систему двух дифференциальных уравнений первого порядка и приводят эту систему к машинному виду (3). Для этого вводится новая неизвестная функция , слева в каждом уравнении системы оставляют только первые производные неизвестных функций, а в правых частях производных быть не должно

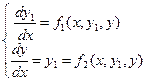(3)

Функция 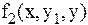в систему (3) введена формально для того, чтобы методы, которые будут показаны ниже, могли быть использованы для решения произвольной системы дифференциальных уравнений первого порядка. Рассмотрим несколько численных методов решения системы (3). Расчетные зависимости для i+1 шага интегрирования имеют следующий вид:

Метод Эйлера.

у1, i+1=у1, i+hf1(xi, y1, i, yi),

уi+1=уi+hf2(xi, y1, i, yi),

xi+1=xi+h.

где h - шаг интегрирования. Начальные условия при численном интегрировании учитываются на нулевом шаге: i=0, x=x0, y1=y1, 0, y=y0. Рассмотрим более подробно порядок составления дифференциальных уравнений и приведения их к машинному виду для описания движения тела на пружинке:

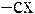Уравнение движения (второй закон Ньютона) для материальной точки с учетом действия сил линейного сопротивления , упругости пружины и синусоидальной силы 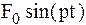может быть записано следующим образом

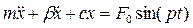, Здесь коэффициент сопротивления; х - координата (х=0 в положении равновесия точки), t - время, p - частота вынужденных колебаний, Fo- амплитуда силы.

Аналитическое решение:

1) Свободные незатухающие колебания:

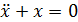
Отсюда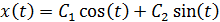

При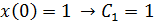

При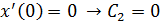

Отсюда общее уравнение имеет вид:

2) Затухающее колебательное движение:

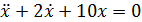
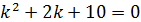
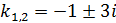
Отсюда

При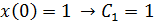

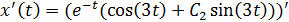
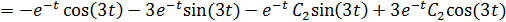
При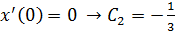

Отсюда общее уравнение имеет вид: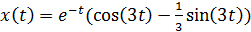

3) Вынужденное колебание без сопротивления

Отсюда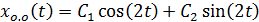

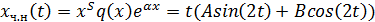
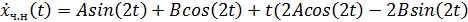
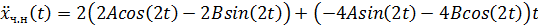
При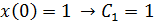

При

Отсюда общее уравнение имеет вид:

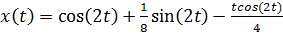
Численное решение:

Вывести численное решение функций при каждом режиме и сравнить с аналитическим решением:

Создадим файл-функцию, описывающую каждый режим:

1) Свободные незатухающие колебания:

function f=f1(t, y1, y)

f=-y;

2) Затухающее колебательное движение:

function f=f1(t, y1, y)

f=-10*y-2*y1;

3) Вынужденное колебание без сопротивления

function f=f1(t, y1, y)

f=sin(2*t)-4*y;

Запишем основной текст программы для каждого режима:

Результатом программы будет график функции. Выведем графики для каждого режима, в соответствии с аналитикой:

1) Свободные незатухающие колебания:

dt=0.0001;

t=0: dt: 20;

y=zeros(1, length(t));

y(1)=1;

y1=zeros(1, length(t));

y1(1)=0;

for i=1: length(t)-1

y1(i+1)=y1(i)+dt*f1(t(i), y1(i), y(i));

y(i+1)=y(i)+dt*y1(i);

end

x=0: 20;

f=cos(x)

figure(1);

hold on

plot(t, y, 'LineWidth', 4);

plot(x, f, 'Marker', 'o', 'LineStyle', 'none', 'Color', 'red', 'LineWidth', 3);

hold off

2) Затухающее колебательное движение:

dt=0.0001;

t=0: dt: 20;

y=zeros(1, length(t));

y(1)=1;

y1=zeros(1, length(t));

y1(1)=0;

for i=1: length(t)-1

y1(i+1)=y1(i)+dt*f1(t(i), y1(i), y(i));

y(i+1)=y(i)+dt*y1(i);

end

x=0: 20;

f=exp(-x).*(cos(3*x)-(1/3)*sin(3*x));

figure(1);

hold on

plot(t, y, 'LineWidth', 4);

plot(x, f, 'Marker', 'o', 'LineStyle', 'none', 'Color', 'red', 'LineWidth', 3);

hold off

3) Вынужденное колебание без сопротивления

dt=0.0001;

t=0: dt: 20;

y=zeros(1, length(t));

y(1)=1;

y1=zeros(1, length(t));

y1(1)=0;

for i=1: length(t)-1

y1(i+1)=y1(i)+dt*f1(t(i), y1(i), y(i));

y(i+1)=y(i)+dt*y1(i);

end

x=0: 20;

f=cos(2*x)+(sin(2*x))/8-(x.*cos(2*x))/4;

figure(1);

hold on

plot(t, y, 'LineWidth', 4);

plot(x, f, 'Marker', 'o', 'LineStyle', 'none', 'Color', 'red', 'LineWidth', 3);

hold off

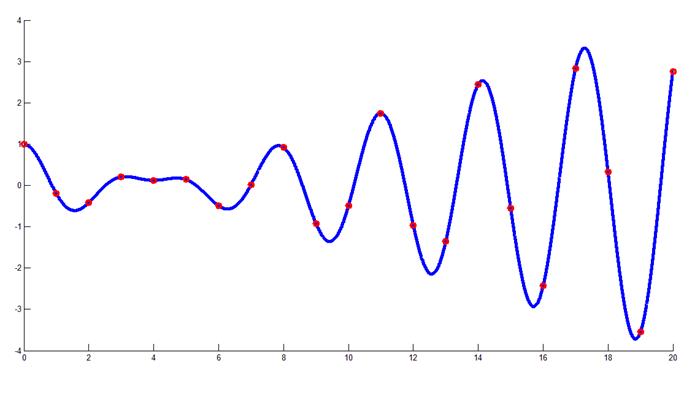
Здесь - аналитическое решение

- численное решение

Вывод:

В данной работе рассмотрели численные методы решения дифференциальных уравнений второго порядка и систем дифференциальных уравнений первого порядка, на примере описания движения материальной точки на пружинке, в среде MatLab.