Baриант 1

1. Плоскость α пересекает стороны АВ и ВС треуголь­ника АВС в точках D и Е соответственно, причем АС || α. Найдите АС, если ВD: AD = 3: 4 и DЕ = 10см.

а) 12, 5 см; б) 7, 5см; в) 24 см; г) 23⅓ см.

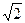2. Отрезок АВ пересекает плоскость α, точка С - середина АВ. Через точки А, В и С проведены параллельные прямые, пересекающие плоскость α в точках А₁, В₁ и С₁. Найдите СС₁, если АА₁ = дм и ВВ₁= дм.

а) 4 дм; б) 4 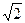дм; в) 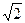дм; г) 2 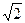дм.

3. Сторону CD треугольника CDE пересекают плоско­сти α и β, параллельные стороне СЕ соответственно в точках К и Р, а сторону DE - в точках М и N, причем DK вдвое меньше РК, а СР вдвое больше РК. Найдите СЕ, если КМ = 6 см.

а) 40 см; б) 36 см; в) 48 см; г) 42 см.

4. AВCDA₁B₁C₁D₁ - прямоугольный параллелепи­пед, АВ = AD = 8 дм, АА₁ = 2 дм. Найдите площадь сечения BMKD, где М - середина В₁С₁ и К - ­середина C₁D_1.

а) 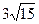см²; б) 12 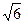см²; в) 6 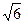см²; г) 15 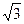см².

5. AВCDA₁B₁C₁D₁ - куб. Точки Е и F – середины ребер АА₁ и СС₁ соответственно. Определите число сторон сечения плоскостью, которая определяется точками В, Е и F.

а) 3; б) 4; в) 5; г) 6.

6. MCDN - ромб, длина стороны которого 4 см; MNKP - параллелограмм. Найдите периметр четы­рехугольника CDKP, если NK = 8 см и СМР = 60⁰.

а) 8(1 + 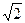)см; б) 6(1 + 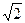)см;

в) 8(1 + 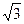)см; г) 12 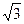см.

7. В треугольной пирамиде МАВС все ребра равны 6 см. Найдите периметр сечения, проведенного паpаллельно стороне ВС и проходящего через точки А и К, где К - середина ВМ.

а) (4 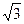+ 3) см; б) 6 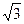см;

в) (6 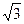+ 1)см; г) 3(2 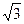+ 1) см.

8. AВCDA₁B₁C₁D₁ - куб. К - середина AD, М – середина CD. В каком отношении, считая от точки А, делит ребро АА₁ плоскость, проходящая через точки В₁, К и М?

а) 1: 1; б) 1: 2; в) 1: 3; г) 1: 4.

Параллельность в пространстве

Вариант 2

1. Плоскость β пересекает стороны МР и КР треуголь­ника МРК соответственно в точках N и Е, причем МК || β. Найдите NE, если МК = 12 см и MN: NP = 3: 5.

а) 8⅓ см; б) 9 см; в) 7, 5 см; г) 8, 5 см.

2. Отрезок CD пересекает плоскость β, точка Е ­- середина CD. Через точки С, D и Е проведены параллельные прямые, пересекающие плоскость β соответственно в точках С₁, D₁ и Е₁. Найдите ЕЕ_1, если СС₁ = 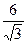см и DD₁ = 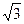см.

а) 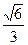см; б) 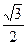см; в) 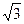см; г) 2 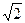см.

3. Плоскости α и β, параллельные стороне АВ треуголь­ника АВС, пересекают сторону АС соответственно в точках N и М, а сторону ВС - в точках Е и К. Отрезок MN в три раза больше отрезка CN, а отрезок АМ вдвое короче MN. Найдите АВ, если NE = 12 см.

а) 64 см; б) 72 см; в) 60 см; г) 66 см.

4. AВCDA₁B₁C₁D₁ - прямоугольный параллелепи­пед, АВ = AD = 12 см, АА₁ = 3 см. Найдите пло­щадь сечения АКЕС, где К – середина A₁B₁ и Е­ - середина B₁C_1.

а) 36 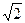см²; б) 27 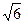см²; в)18 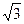см²; г) 24 см²..

5. AВCDA₁B₁C₁D₁ - куб, Е - середина CC_1. Опреде­лите число сторон сечения плоскостью, которая проходит через точки А, В₁ и Е.

а) 3; б) 4; в) 5; г) 6.

6. CDEK - ромб, сторона которого равна 8 см, CKMN - параллелограмм. Найдите периметр четы­рехугольника DЕМN, если КМ = 6 см и DCN = 60⁰.

а) 4(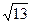 + 4) см; б) 6( 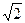+ 3) см;

в) 8 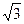см; г) (2 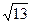+ 15) см.

7. В треугольной пирамиде SMEF все ребра равны 4 см. Найдите периметр сечения, проведенного параллельно ребру МF и проходящего через точки Е и Р, где Р - середина отрезка SF.

а) 3(2 + 3 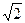)см; б) 6(3 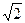+ 1) см;

в) 2(1 +2 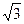) см; г) 6 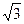см.

8. AВCDA₁B₁C₁D₁- куб, точка Е - середина CD, F делит ребро AD в отношении 1: 3, считая от точки D. В каком отношении делит ребро АА₁ (считая от точки А) плоскость, проходящая через точки В₁, Е и F?

а) 1: 2; б) 2: 1;.в) 2: 3; г) 3: 2.