Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Явления на границе жидкости и твердого тела
|
|
Твердые тела, как и жидкости, обладают поверхностным натяжением.
При рассмотрении явлений на границе раздела различных сред следует иметь в виду, что поверхностная энергия жидкости или твердого тела зависит
- не только от свойств данной жидкости или твердого тела,
- но и от свойств того вещества, с которым они граничат.
Рис. 6.
 |
Строго говоря, нужно рассматривать суммарную поверхностную энергию двух граничащих друг с другом веществ Только если одно вещество газообразно, химически не реагирует с другим веществом и мало в нем растворяется, можно говорить просто о поверхностной энергии (или коэффициенте поверхностного натяжения) второго жидкого или твердого тела.
|
|
Из рис. 7 следует, что условие равновесия элемента контура длиной ∆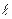 
запишется следующим образом:
,
где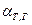 
, 
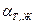и 
— коэффициенты поверхностного натяжения на границах: 
твердое тело — газ, твердое тело — жидкость и жидкость — газ.
Отсчитываемый внутри жидкости угол 
между касательными к поверхности твердого тела и к поверхности жидкости называется краевым углом:
(5)
Краевой угол определяется выражением (5) только при условии, что
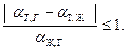(6)
Если это условие не выполняется, т. е. | α т, г — α т, ж | > α ж, г, ни при каком значении не может установиться равновесие. Это имеет место в двух случаях.
1) α т, г > α т, ж + α ж, г. (рис. 9. а).
- Как бы ни был мал угол , сила α т, г перевешивает две другие
- В этом случае жидкость неограниченно растекается по поверхности твердого тела — имеет место полное смачивание. Замена поверхности твердое тело — газ двумя поверхностями, твердое тело — жидкость и жидкость — газ, оказывается энергетически выгодной.
- При полном смачивании краевой угол равен нулю.
2 ) α т, ж > α т, г + α ж, г. (рис. 9. б).
- Как бы ни был угол близок к π, сила α т, ж перевешивает две другие
|
 |
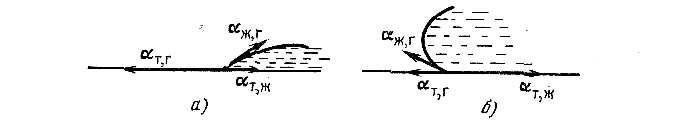- Замена поверхности твердое тело — жидкость двумя поверхностями, твердое тело — газ и жидкость — газ, оказывается энергетически выгодной.
- При полном несмачивании краевой угол равен π.
При соблюдении условия (6) краевой угол может оказаться острым или тупым в зависимости от соотношения между α т, г и α т, ж.
- Рис. 10.а). Если α т, г больше, чем α т, ж, то cos > 0 и угол — острый
В этом случае имеет место частичное смачивание.
-
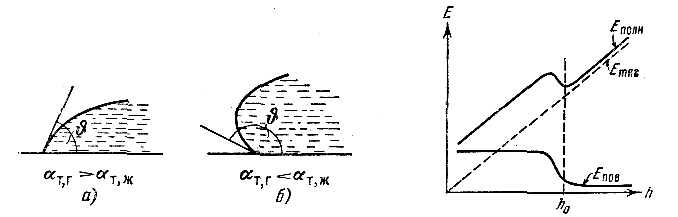
Рис. 10. б). Если α т, г меньше, чем α т, ж, то cos < 0 и угол — тупой.
В этом случае имеет место частичное несмачивание.
|
|
ПРИМЕР:
1. Известно, что смазанная жиром иголка или бритвенное лезвие могут держаться на поверхности воды.
Объяснение этого, на первый взгляд удивительного, явления проще всего дать, исходя из энергетических соображений:
-. Смазанная жиром поверхность стали не смачивается водой; поверхность соприкосновения сталь — вода обладает гораздо большей энергией, чем поверхность сталь — воздух или воздух — вода.
- Полное погружение иглы в воду сопровождается увеличением поверхностной энергии от значения Sα т, г (сталь —воздух) до значения Sα т, ж (сталь — вода), где S — поверхность иглы.
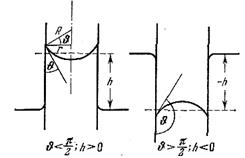
- Изменение поверхностной энергии при погружении описывается изображенной на рис. 11 кривой Eпов. Буквой h обозначена высота иглы над дном сосуда;
h 0 — высота поверхности жидкости над уровнем дна.
Зависимость от h потенциальной энергии иглы в поле земного тяготения E тяг имеет вид прямой, проходящей через начало координат.
- Полная энергия E полн, равная сумме E пов и E тяг, имеет минимум при h = h 0, что и дает возможность игле плавать на поверхности воды.
- Если, нажав па иглу, погрузить ее на такую глубину, чтобы полная энергия прошла через максимум и стала уменьшаться, то игла дальше будет погружаться сама и утонет.
2. Аналогично объясняется возможность «носить воду в решете».
|
8.5. Капиллярные явления
Существование краевого угла приводит к тому, что вблизи стенок сосуда наблюдается искривление поверхности жидкости.
Рис. 13. В узкой трубке (капилляре) или в узком зазоре между двумя стенками искривленной оказывается вся поверхность.
· 
Если жидкость смачивает стенки, поверхность имеет вогнутую форму,
· если не смачивает - выпуклую.
|
Если капилляр погрузить одним концом в жидкость, налитую в широкий сосуд, то под искривленной поверхностью в капилляре давление будет отличаться от давления под плоской поверхностью в широком сосуде на величину ∆ р, определяемую формулой (4). В результате
- при смачивании капилляра уровень жидкости в нем будет выше, чем в сосуде,
- при несмачивании — ниже.
Изменение высоты уровня жидкости в узких трубках или зазорах получило название капиллярности.
В широком смысле под капиллярными явлениями понимают все явления, обусловленные существованием поверхностного натяжения.
Между жидкостью в капилляре и широком сосуде устанавливается такая разность уровней h, чтобы гидростатическое давление ρ gh уравновешивало капиллярное давление ∆ p:
(7)
В этой формуле α — поверхностное натяжение на границе жидкость — газ,
R — радиус кривизны мениска.
Радиус кривизны мениска R можно выразить через краевой угол и радиус капилляра r.
из рис. 13 видно, что R = r/ cos .
Подставив это значение в (7) и выразив h, получаем
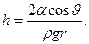(8)
В соответствии с тем, что
- смачивающая жидкость поднимается по капилляру,
- а несмачивающая — опускается,
Формула (8) дает в случае
- < π /2 (cos > 0) положительные h
- > π /2 (cos < 0) отрицательные h.
|
Формулу для h можно получить также на основании энергетических соображений, причем не возникает необходимости делать какие-либо специальные предположения о форме мениска.
- Равновесное положение мениска будет соответствовать минимуму энергии Е системы жидкость — капилляр.
- Эта энергия слагается из поверхностной энергии на границах жидкость — стенка, жидкость — газ и стенка — газ, а также из потенциальной энергии жидкости в поле земного тяготения.
Рис. 14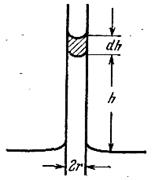 
. Найдем, приращение энергии dE, соответствующее приращению высоты поднятия жидкости в капилляре dh.
- При возрастании высоты на dh поверхность соприкосновения жидкости со стенкой капилляра увеличивается на 2 π rdh
- вследствие чего энергия получает приращение, равное 2 π rα т, ж dh.
- Одновременно уменьшается поверхность соприкосновения стенки с газом, что сопровождается приращением энергии, равным — 2 π rα т, г dh.
- Потенциальная энергия в поле земного тяготения получает приращение, равное силе тяжести, действующей на заштрихованный объем жидкости умноженной на h, т. е. равное gρ π r 2 hdh.
- Изменением уровня жидкости в широком сосуде можно пренебречь. Таким образом,
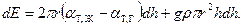
Отсюда следует, что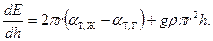 
Приравняв эту производную нулю, получим условие равновесия, из которого вытекает, что
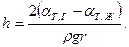
В соответствии с формулой (5) α т, г — α т, ж = α ж, г cos .
Произведя такую замену и обозначив α ж, г как α, получим формулу (8).