Теоретические сведения

Цель работы

1.1 Изучение процесса умножения частоты в заданное число раз, исследование электрической схемы умножителя частоты.

1.2 Получение практических навыков исследовательской работы с комплексом контрольно-измерительного лабораторного оборудования.

Домашнее задание

Изучите:

2.1 Принцип умножения частоты (Л стр. 243-244, Л3 стр. 86-87)

2.2 Методы анализа нелинейных цепей. Преобразование сигналов при прохождении через нелинейные цепи (Л1 стр.231-243)

2.3 Методическое пособие данной работы.

2.4 Подготовьте бланк отчета.

Содержание отчета

Отчет должен содержать титульный лист установленной формы, цель ра­боты, рис. 5.2, 5.3, 5.4, таблица 6.1, вывод по работе.

Вопросы допуска к выполнению работы

4.1 Объясните принцип умножения частоты.

4.2 Для чего осуществляют умножение частоты?

4.3 Какие контрольно-измерительные приборы используются в данной работе? Дайте краткую характеристику каждому прибору.

Теоретические сведения

5.1 Принцип умножения частоты

Он состоит в получении из гармонического колебания с частотой ω ₀ другого гармонического колебания, с частотой n·ω _о, где n – целое положительное число, т.е. если

S₁(t) = U_вх cos (ω ₀t + φ), то S₂(t) = U_вых cos (nω ₀t +φ), временное и спектральное изображение представлено на рис.5.1, при n=2.

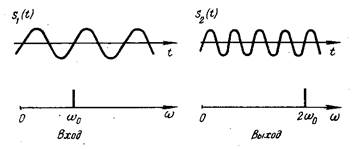
Рис.5.1 К пояснению процесса умножения

Умножение частоты используется в различной аппаратуре и, в частности, в радиопередающих устройствах.

5.2 Электрическая схема умножителя частоты

Для умножения частоты используют устройство, называемое умножителем частоты, на выходе которого получаются колебания с частотой, в целое число раз большей частоты входного сигнала. На рис. 5.2 представлена электрическая схема умножителя частоты.

В качестве нелинейного элемента в схеме используют биполярный транзистор VT, у которого нелинейной является характеристика i_k = f (u_бэ), т.е. ток коллектора зависит от напряжения между базой и эмиттером u_бэ. Гармоническое колебание u (t) c частотой ω, на которую настроен входной колебательный контур L₁C₁, приложено к переходу база –эмиттер и управляет током коллектора в выходной цепи. Источник напряжения смещения U₀ обеспечивает требуемое положение рабочей точки на характеристике i_k = f (u_бэ).

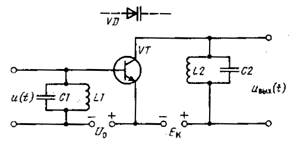
Рис. 5.2 Упрощенная электрическая схема умножителя частоты

Контур L₂C₂ в выходной цепи настроен на частоту нужной гармоники nω тока коллектора i_k(t). Если добротность контура достаточно велика, то напряжение u_вых (t) пропорционально току этой гармоники и является гармоническим колебанием с частотой nω. Остальные гармоники тока коллектора отфильтровываются, т.к. сопротивление контура на их частотах практически равно нулю.

Обратим внимание на то, что с увеличением коэффициента кратности n максимальная амплитуда n-ой гармоники тока уменьшается. Поэтому схема (рис.5.2) используется для умножения частоты в 2, 3, 4 раза. Для получения больших значений коэффициента кратности n такие схемы включают друг за другом последовательно. Например, для достижения n=12 ставят два каскада: один с коэффициентом кратности n₁ = 4 и второй с коэффициентом кратности n₂ = 3 или три каскада с n₁ = 2 n₂ = 2 n₃ = 3.

Умножение частоты – это задача, в результате решения которой должна быть найдена характеристика нелинейного элемента, осуществляющего умножение частоты в заданное число раз. На практике при больших уровнях входных сигналов ВАХ несимметричного нелинейного элемента целесообразно представить в виде кусочно-ломаной прямой (метод линеаризации), состоящей из двух отрезков прямых линий как показано на рис.5.3, то ток в нелинейной цепи существует только в течение некоторой части периода входного напряжения. Эта часть периода определяется соотношением между амплитудой входного сигнала U_m и напряжением U₀.

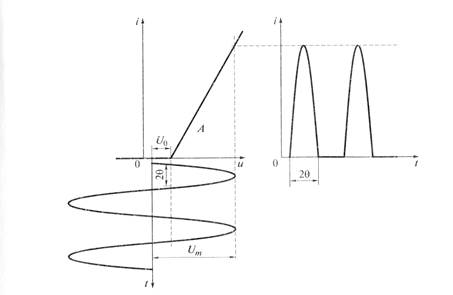
Рис.5.3. Форма тока в цепи, содержащей нелинейный элемент, полученная путем аппроксимации ВАХ кусочно-ломаной прямой

В этом случае говорят, что устройство работает в режиме отсечки, а напряжение U₀ называют напряжением отсечки. Т.к. весь период гармонического колебания соответствует повороту характеризующего его вектора на 360^о, то часть периода, в течение которого в цепи течет ток, также можно характеризовать угловой мерой, но меньшей 360^о.Такой мерой является угол отсечки θ, который определяется из соотношения U_mcos θ = U₀, т.е. θ = arсcos(U₀/U_m). Физический смысл угла отсечки иллюстрирует рис. 5.3. Если U₀ = 0, то θ = 90^о и выходной ток существует в течение полупериода. С увеличением U₀ до U_m угол отсечки уменьшается от 90^о до 0^о и, следовательно, время протекания тока сокращается. При этом меняются форма импульса тока и амплитуда гармоник, составляющих этот импульс. Таким образом, при гармоническом воздействии ток i(t) имеет импульсный характер, остальная часть гармонического колебания как бы отсекается, поэтому такой режим работы нелинейного элемента называется режимом с отсечкой, а параметр θ углом отсечки.

Для характеристики изменений амплитуд гармоник при изменении угла отсечки от 0^о до 180^о советским ученым в области радиотехники, академиком А.И. Бергом были введены коэффициенты пропорциональности между амплитудами гармоник I_mk и амплитудой усеченного синусоидального импульса I_m, названные впоследствии коэффициентами Берга или коэффициентами постоянной составляющей первой, второй и прочих гармоник. Коэффициенты гармоник представляют нормированные амплитуды спектральных составляющих тока и определяют влияние угла отсечки на амплитуду соответствующей гармоники: α ₀ (θ) = I₀ /I_max; α ₁ (θ) = I₁ /I_max; α _n (θ) = I_n /I_max;

Значения коэффициентов Берга можно найти из специальных таблиц или графиков (рис.5.4).

Рис.5.4. Графики некоторых коэффициентов Берга

При использовании этих графиков амплитуда n-й гармоники тока определяется как

I_n = α _n(θ)I_max. Из графиков следует, что при неизменном I_max максимальная амплитуда какой либо гармоники достигается при некотором оптимальном угле θ _опт = 120^о /n.

Если θ = 0, то нелинейный элемент закрыт на протяжении всего периода Т действия гармонического напряжения u(t), поэтому i(t) = 0.

Если θ = 180^о, то отсечка отсутствует и форма тока практически совпадает с с формой напряжения. В результате ток i(t) содержит постоянную составляющую I₀ и первую гармонику. Амплитуды всех остальных гармоник равны нулю. Графики на рис.5.4 позволяют выбирать оптимальное значение угла отсечки θ для получения наибольшей амплитуды нужной гармоники тока. Так при удвоении частоты θ = 60^о, а при утроении θ = 40^о