Алгоритмы оптимального когерентного приема для правила максимального правдоподобия.

При использовании алгоритма оптимального когерентного приема для правила максимального правдоподобия необходимо помнить, что данное правило реализует критерий идеального наблюдателя при том условии, что все символы передаются равновероятно.

Правило решения (5) можно записать иначе, воспользовавшись формулой Байеса (3) p (b_l) w (z ½ b_l)> p (b_r) w (z ½ b_r) или

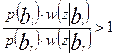. (6)

Выражение (6) используется при выборе решения для финитного спектра сигнала z (t).

При полном использовании сигнала оптимальное правило решения (6) по критерию идеального наблюдателя запишется:

, (7)

где 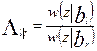- отношение правдоподобия символа b_l относительно b_r.

В частном случае, когда все символы передаются с одинаковыми априорными вероятностями p (b_r)= p (b_l)=1/ m, неравенство (7) упрощается:

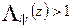. (8)

Выражение (8) является оптимальным правилом решения и называется правилом максимального правдоподобия, применяемое практически во всех системах связи, так как все кодовые символы в них передаются примерно с одинаковыми вероятностями.

Еще чаще приходится встречаться с такой ситуацией, когда при проектировании системы связи вообще нет данных об априорных вероятностях различных кодовых символов. Так, например, при сооружении кабельной линии зачастую неизвестно, какие потребители будут ее использовать, и какого рода сообщения передавать. Поэтому правило (6) применять нельзя, так как известны только входящие в него величины w (z ½ b_r), которые определяются свойствами канала, но неизвестны p (b_r), определяемые свойствами источника.

В таких условиях целесообразно пользоваться правилом максимального правдоподобия (8).

Рассмотрим вывод формулы для построения оптимального когерентного приемника. Для наглядности воспользуемся структурной схемой системы передачи информации (см. лекцию 5/34).

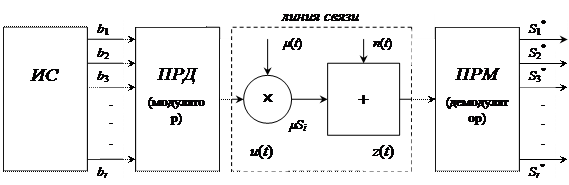Рис. 1. Структурная схема системы передачи информации

Напряжение на входе приемника

z (t) =m s_i (t - t) +n (t), 0£ t £ T, (9)

зависит только от аддитивной помехи, так как при когерентном приеме все параметры сигнала известны. Помеха имеет случайный характер и подчиняется нормальному закону распределения:

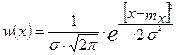, (10)

а значит и напряжение на входе приемника, также будет подчиняться нормальному закону.

Известно, что копии c ₁ и c ₂ сигналов s ₁ и s ₂ определяются:

Условные плотности вероятности для s ₁ и s ₂ будут равны:

, (12)

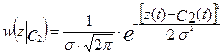. (13)

Найдем отношение правдоподобия между реализациями по формуле (8):

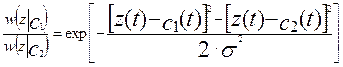(14)

где z (t) – напряжение на входе приемника; c ₁ и c ₂ – копии сигналов s ₁ и s ₂; s² – средняя мощность шума.

Избавимся от exp

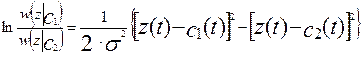(15)

Проинтегрировав и усреднив его за время действия одной реализации, равное периоду получим правило принятия решения в пользу реализации s ₁.

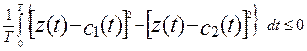(16)

Полученное преобразуем:

(17)

В формуле (17) реализуется признак минимального среднеквадратичного отклонения, то есть в сигнале z(t) распознается та реализация (s ₁ или s ₂) относительно которой отношение [ z (t)- c _{1, 2}(t)]² будет меньшим.

Преобразуем (17) и получим:

(18)

Зная, что: ; 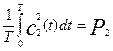, где P ₁ и P ₂ – средняя мощность реализации сигнала на входе приемника определим:

(19)

Полученный критерий позволяет синтезировать схему оптимального когерентного приемника.

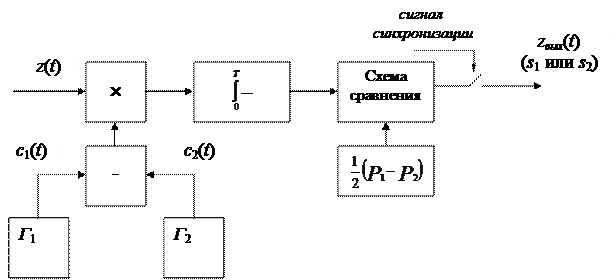
Рис. 1. Структурная схема оптимального когерентного приемника

Назначение элементов схемы и принцип работы схемы. Г ₁ и Г ₂ вырабатывают точные копии c ₁и c ₂ соответствующие реализациям s ₁ и s ₂ поступают на вход вычитателя. Результирующий сигнал поступает на вход умножителя, на второй вход которого поступает входной сигнал z (t). Преобразованный сигнал интегрируется в интеграторе и поступает на вход схемы сравнения. На второй вход которого поступает сигнал u_пор.

- Если u_инт > u_пор то, схема принимает решение, что был передан сигнал s ₁ (" 1");

- Если u_инт < u_пор то, схема принимает решение, что был передан сигнал s ₂ (" 0").

Подбором u_пор (D u) достигается правильность принятия решения на определение соответствующей копии сигнала. u_пор может устанавливаться автоматически и зависеть только от входной мощности сигнала.

Заключение

Для построения схемы оптимального когерентного приемника применяются алгоритмы для правил максимальной апостериорной вероятности и максимального правдоподобия. В свою очередь последнее используется лишь в том случае, когда все символы сообщения передаются равновероятно.

Разработал

Доктор военных наук, профессор

А. Привалов