
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Алгоритм решения.Пусть a b 0 и a > 0
|
|
Алгоритм решения. Пусть a 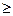 b
b 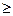 0 и a > 0. Тогда применение алгоритма Евклида происходит так: если b = 0, то НОД(a, b) = a. Иначе вычисляем r, равное остатку от деления a на b, и сводим задачу отыскания НОД(a, b) к задаче отыскания НОД(r, b). При r> 0 этот процесс можно продолжить. Имеем: b > r > r1 > r2 > r3 >,..., но так как b, r, r1, r2, r3 - неотрицательные целые числа, то найдется n такое, что rn = 0. В соответствии с высказанным утверждением
0 и a > 0. Тогда применение алгоритма Евклида происходит так: если b = 0, то НОД(a, b) = a. Иначе вычисляем r, равное остатку от деления a на b, и сводим задачу отыскания НОД(a, b) к задаче отыскания НОД(r, b). При r> 0 этот процесс можно продолжить. Имеем: b > r > r1 > r2 > r3 >,..., но так как b, r, r1, r2, r3 - неотрицательные целые числа, то найдется n такое, что rn = 0. В соответствии с высказанным утверждением
НОД(a, b) = НОД(b, r) = НОД(r1, r) =... = НОД(rn-1, 0) = rn-1.
Практически это выглядит так. Надо найти НОД чисел 888 и 351.
Большим из них является 888, a = 888, b = 351.
Находим остаток от деления a на b: 888 mod 351 = 186, r = 186;
заменим a на b и b на остаток r, получим: a = 351, b = 186;
снова находим остаток от деления a на b: 351 mod 186 = 165, r = 165;
заменим a на b и b на остаток r, получим: a = 186, b = 165;
находим остаток от деления a на b: 186 mod 165 = 21, r = 21;
заменим a на b и b на остаток r, получим: a = 165, b = 21;
находим остаток от деления a на b; 165 mod 21 = 18, r = 18;
заменим a на b и b на остаток r, получим: a = 21, b = 18;
находим остаток от деления a на b; 21 mod 18 = 3, r = 3;
заменим a на b и b на остаток r, получим: a = 18, b = 3;
находим остаток от деления a на b: 18 mod 3 = 0, r = 0;
заменим a на b и b на остаток r, получим: a = 3, b = 0.
Как только b стало равным нулю, цикл заканчивается, выдается значение a, которое и является наибольшим общим делителем, НОД(888, 351) = a = 3.
Этот процесс можно записать в виде следующей цепочки, которая в общем виде была записана выше:
НОД(888, 351) = НОД(351, 186) = НОД(186, 165) =
= НОД(165, 21) = НОД(21, 18) = НОД(18, 3) = НОД(3, 0) = 3.
Program Problem12; { Алгоритм Евклида }
uses WinCrt;
var
a, b, r, a1, b1: integer;
begin
write('Введите первое число '); readln(a);
write('Введите второе, не равное нулю, число ');
readln(b);
a1: = a; b1: = b;
repeat
r: = a mod b;
a: = b; b: = r
until b = 0;
writeln('НОД чисел ', a1, ' и ', b1, ' равен ', a)
end.