Указания по выполнению ГР № 3

Выполнение контура технической детали с применением геометрических построений.

Работа выполняется на формате А3 (см. образец работы). На формате выполняют рамку и основную надпись.

При выполнении работы студент должен помнить, что для изображения изделий на чертежах применяют линии различных типов в зависимости от их назначения (ГОСТ 2.303-68).

При вычерчивании контура технической детали студент должен знать правила выполнения геометрических построений: сопряжение дуги с дугой, дуги с прямой, деление окружности на равные части, а также основные правила нанесения размеров (ГОСТ 2.307-68).

ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ

В основе построения правильных различных многоугольников лежит деление описанной вокруг них окружности на равные части.

ДЕЛЕНИЕ ОКРУЖНОСТИ НА ТРИ, ШЕСТЬ И ДВЕНАДЦАТЬ ЧАСТЕЙ

В окружности заданного радиуса R проводят через центр О взаимно перпендикулярные оси АВ и CD. Из любой части конца диаметра (например, А) проводят радиусом R дугу до пересечения с окружностью в точках 1 и 2.

Отрезок 12 – искомая сторона правильного вписанного треугольника 1В2.

В свою очередь, отрезки А1 = А2 и С1 = С2 соответственно равны сторонам правильных вписанных шестиугольника и двенадцатиугольника.

ДЕЛЕНИЕ ОКРУЖНОСТИ НА ПЯТЬ И ДЕСЯТЬ ЧАСТЕЙ

Проводят два взаимно перпендикулярных диаметров AB и CD и делят радиус ОВ пополам в точке О₁. Из точки О_1, как из центра, проводят дугу радиусом О₁С до пересечения её с диаметром АВ точке М.

Отрезок СМ равен стороне правильного вписанного пятиугольника, отрезок ОМ – сторона десятиугольника.

ДЕЛЕНИЕ ОКРУЖНОСТИ НА СЕМЬ ЧАСТЕЙ

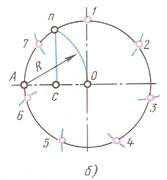
Из точки А проводится вспомогательная дуга радиусом R, равным радиусу данной окружности, которая пересечет окружность в точке п. Из точки п опускают перпендикуляр на горизонтальную осевую линию. Из точки 1 радиусом пс, делают по окружности семь засечек и получают семь искомых точек.

СОПРЯЖЕНИЯ

Сопряжением называется плавный переход одной линии в другую.

Для правильного выполнения сопряжения на чертежах необходимо знать приемы их построения:

1) Прямая, касательная к окружности, образует прямой угол с радиусом, проведенным в точку касания.

2) Точка касания двух окружностей всегда лежит на прямой линии, соединяющей центры окружностей.

Центр сопрягающей дуги О и точки касания А и В находятся геометрическим построением, как показано на рисунках.

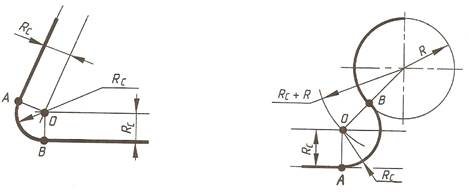
Сопряжение между двумя прямыми Сопряжение прямой и дуги

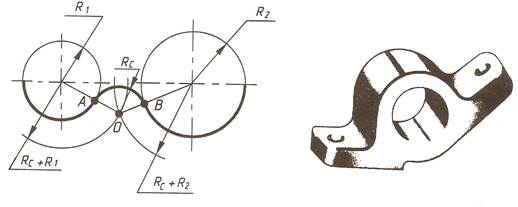
Внешнее сопряжение двух дуг

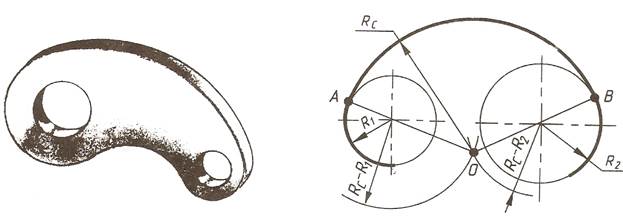
Внутреннее сопряжение двух дуг

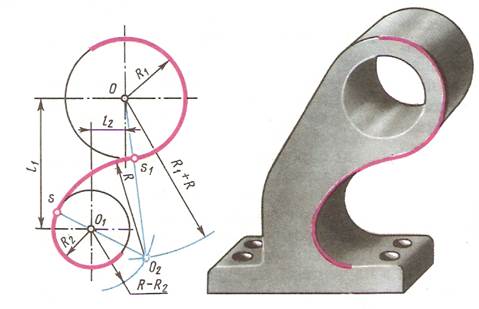
Смешанное сопряжение двух дуг