
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Указания по выполнению ГР № 5
|
|
Построение проекций геометрического тела усеченного плоскостью. Построение натуральной величины сечения, развертки, изометрии усеченного геометрического тела (призмы, пирамиды, цилиндра, конуса).
Чертежи выполняются на формате А3.
Работа выполняется в пять этапов.
Первый этап – построение комплексного чертежа геометрического тела.
Второй этап – проведение следов секущей плоскости. Следует обратить внимание на то, что проекция геометрического тела, отсеченная следом, показывается тонкой сплошной линией. Отметить точки пересечения геометрического тела с секущей плоскостью и найти проекции этих точек на трех видах геометрического тела. Соединить точки и получить проекции сечения на трех видах.
Третий этап – нахождение натуральной величины фигуры сечения способом замены плоскостей проекций.
Четвертый этап – построение развертки усеченного тела. Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга). Выполнение развертки начинается с построения боковой поверхности, к которой пристраивают фигуру нижнего основания, а затем фигуру с сечением. Линия сгиба на развертке показывают штрихпунктирной линией с двумя точками.
Пятый этап – построение геометрической фигуры в изометрии по координатам.
ПОСТРОЕНИЕ РАЗВЕРТОК
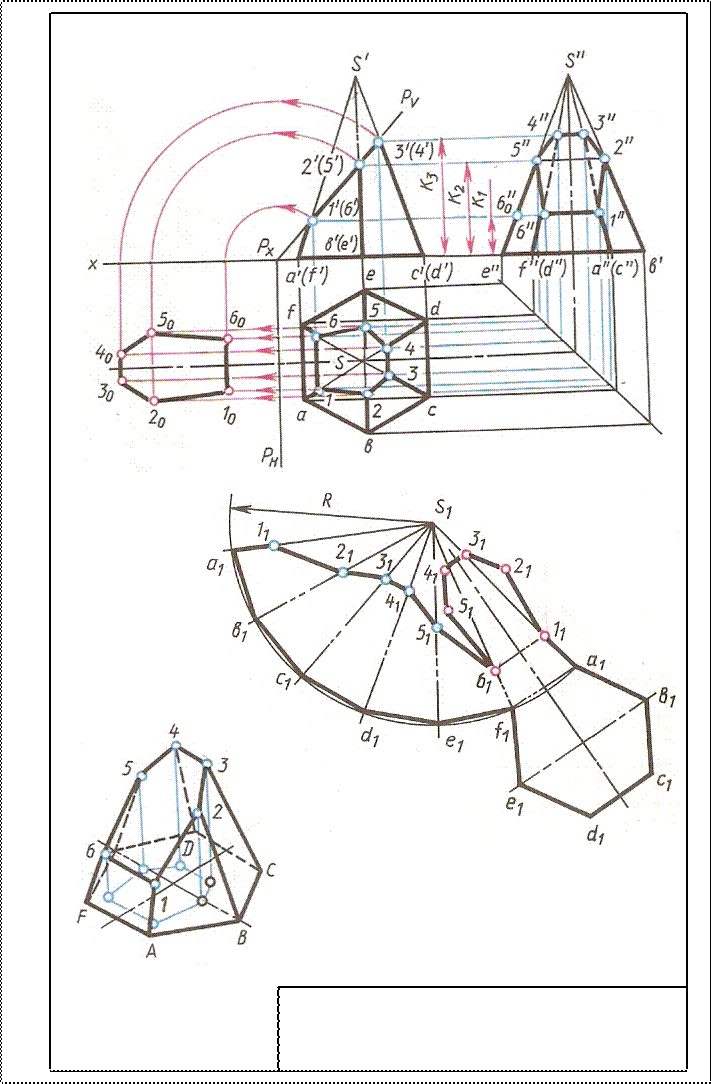
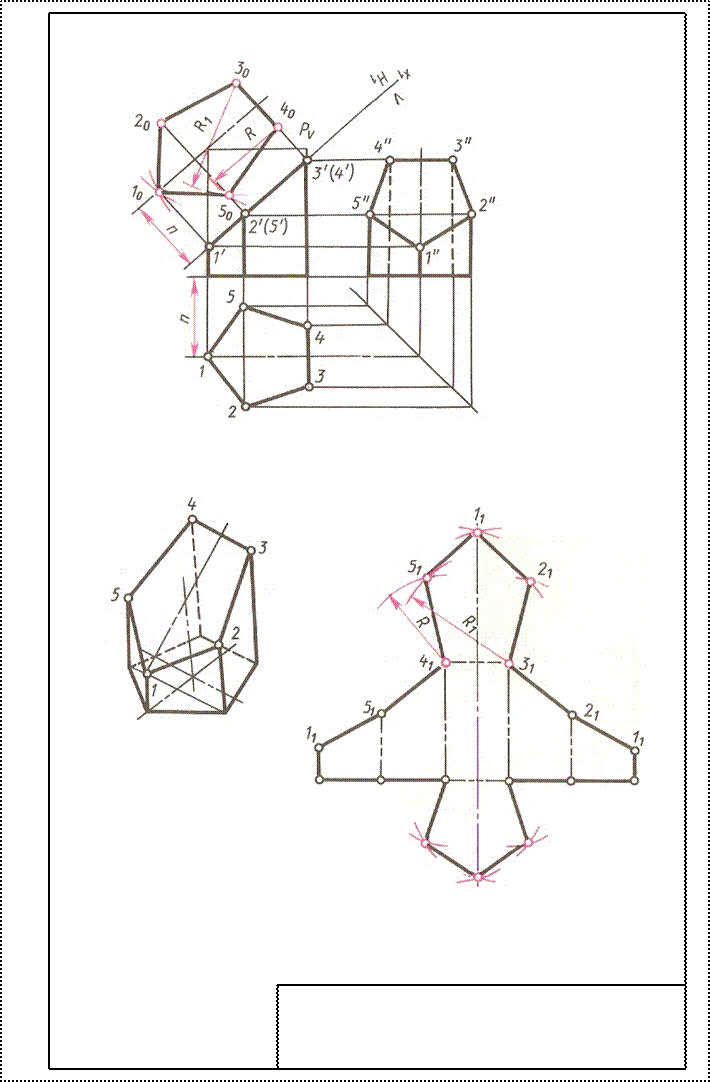
Развертка призмы: Развертку боковой поверхности с основанием и фигурой сечения призмы строят следующим образом. Проводят прямую, на которой откладывают пять отрезков, равных длинам сторон пятиугольника, лежащего в основании призмы. Из полученных точек проводят перпендикуляры, на которых откладывают действительные ребра, усеченной призмы, беря их фронтальной или профильной проекции.
Получают развертку боковой поверхности призмы. К развертке боковой поверхности пристраивают фигуру нижнего основания – пятиугольник и фигуру сечения.
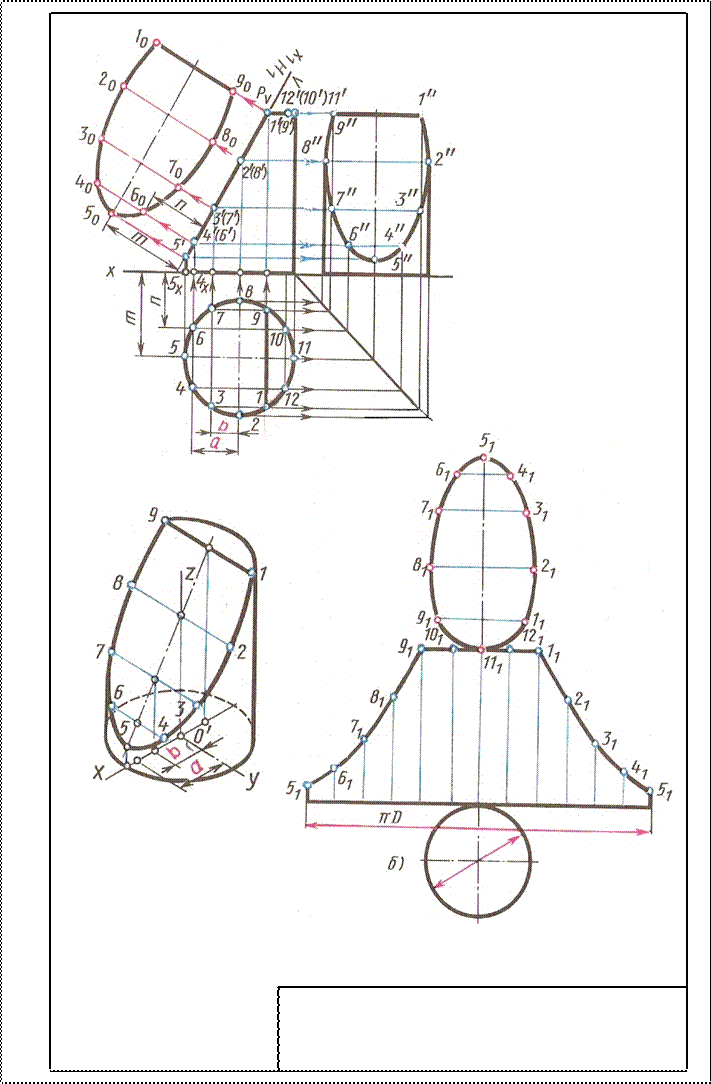
Развертка цилиндра: Для построения развертки боковой поверхности на горизонтальной прямой откладывают длину окружности основания, равную π D и делят её на 13 равных частей. Из точек деления восставляют перпендикуляры к отрезку π D, на них откладывают действительные длины образующих цилиндра от основания до секущей плоскости Р, которые взяты с фронтальной или профильной проекции цилиндра. Полученные точки соединяют по лекалу плавной кривой. Затем фигуру сечения соединяют с частью верхнего основания цилиндра, ограниченного хордой, а фигуру нижнего основания (окружность) соединяют с нижней частью развертки.
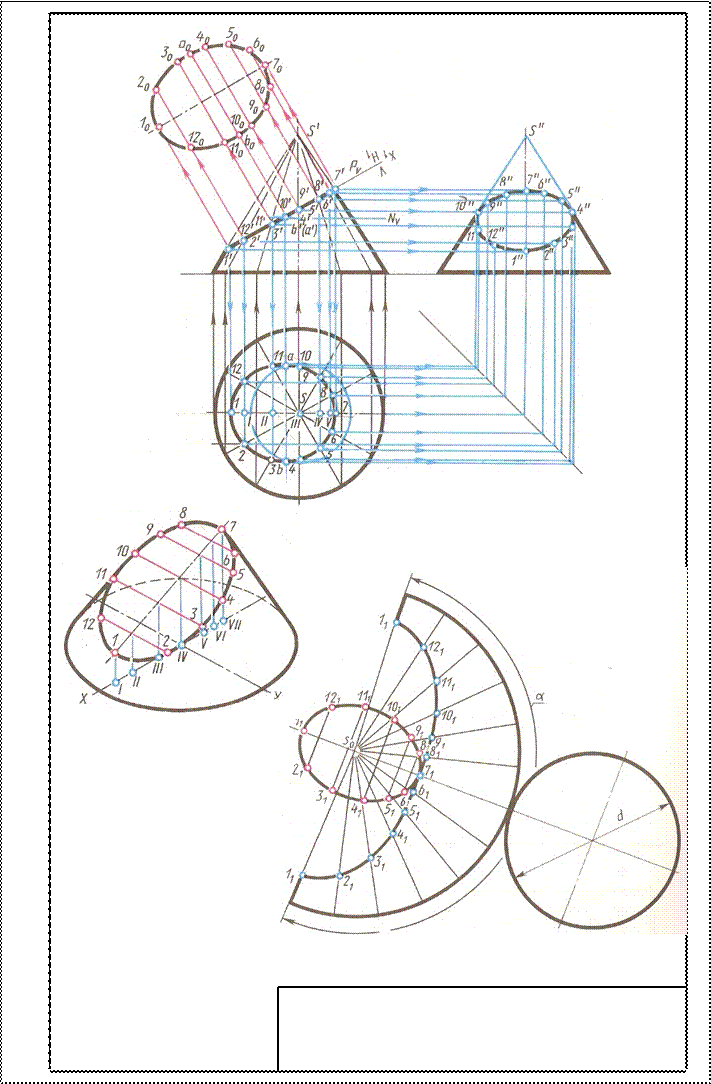
Развертка конуса: Построение развертки поверхности конуса начинают с проведения дуги окружности радиусом, равным длине образующей конуса из точки Sо. Длина дуги определяется углом α: α = 180о х(d / l) где d – диаметр окружности основания конуса; l – длина образующей конуса.
Дугу делят на 12 частей и получают точки соединения с вершиной Sо. От вершины откладывают действительные длины отрезков образующих от вершины конуса до секущей плоскости Р.
Действительные длины этих отрезков находят, как в примере с пирамидой, способом вращения около вертикальной оси, проходящей через вершину конуса.
К развертке конической поверхности пристраивают фигуру сечения и основания конуса.
Сечение пирамиды: Сначала строится развертка неусеченной пирамиды, все грани которой, имеющие форму треугольника одинаковы.
 | |||||
 | |||||
 | |||||
 | |||||
 | |||||
 | |||||
|