
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сложение и разложение сил. Проекция силы на ось и на плоскость.
|
|
СИСТЕМА СХОДЯЩИХСЯ СИЛ
В соответствии с аксиомой сложения сил, две силы, приложенные к одной точке можно заменить одной — равнодействующей, которая находится по правилу параллелограмма или по правилу треугольника. Легко обобщить это правило на тот случай, когда к одной точке приложено более двух сил. Для нахождения их равнодействующей необходимо из конца первого вектора провести второй вектор и т. д. Поясним это на рис.2.11.
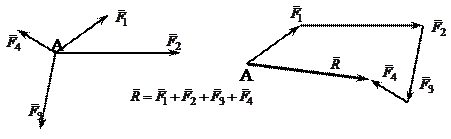
Рис.2.11 Равнодействующая сходящейсясистемы сил
Полученный многоугольник называется силовым, замыкающая сторона которого — вектор 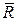 , определяет вектор равнодействующей, направлен из начала первого вектора силы в конец последнего вектора силы.
, определяет вектор равнодействующей, направлен из начала первого вектора силы в конец последнего вектора силы.
Решение задачи об определении суммы нескольких векторов (вектора 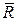 ) является единственным и не зависит от того, в каком порядке складываются слагаемые векторы.
) является единственным и не зависит от того, в каком порядке складываются слагаемые векторы.

Рис.2.12 Разложение силы на составляющие
Противоположный по смыслу алгоритм — разложение векторов, не имеет единственного решения, до тех пор, пока не заданы сами направления разложения сил.
Например, силу 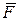 , расположенную в плоскости (рис.2.12), можно разложить по взаимно перпендикулярным осям
, расположенную в плоскости (рис.2.12), можно разложить по взаимно перпендикулярным осям 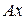 и
и 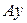 , а можно и по любым другим
, а можно и по любым другим 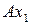 и
и 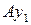 , При этом на оси
, При этом на оси 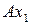 и
и 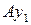 , наложено всего одно условие — они не должны быть параллельны друг другу. Cилы
, наложено всего одно условие — они не должны быть параллельны друг другу. Cилы 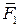 и
и 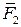 или
или 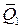 и
и 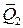 называются составляющими силы
называются составляющими силы 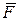 .
.
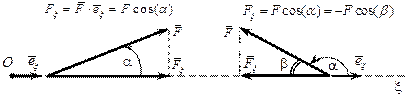
Рис.2.13 Проекции силы на плоскости
Рассмотрим понятие проекции силы на ось. Проекцией силы на заданную ось, например 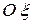 , называется скалярное произведение вектора силы
, называется скалярное произведение вектора силы 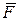 на единичный вектор
на единичный вектор  , характеризующий положительное направление оси, т. е.
, характеризующий положительное направление оси, т. е.
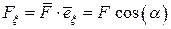
Угол 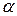 находится между положительным направлением оси
находится между положительным направлением оси 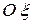 и направлением вектора силы
и направлением вектора силы 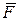 . В том случае, когда
. В том случае, когда 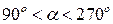 проекция
проекция 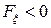 , т. к.
, т. к. 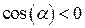 . Модуль этой проекции удобно вычислять через угол
. Модуль этой проекции удобно вычислять через угол 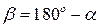 . В соответствии с определением проекции силы
. В соответствии с определением проекции силы 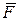 и скалярного произведения векторов можно записать
и скалярного произведения векторов можно записать
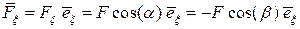
Вернемся к вопросу о разложении силы и рассмотрим эту процедуру в пространственном случае. Часто встречаются два варианта разложения: в первом случае (рис.2.13 а) ориентация вектора в пространстве задана двумя углами 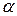 — между осью
— между осью 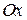 и направлением составляющей силы
и направлением составляющей силы 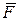 , лежащей в плоскости
, лежащей в плоскости 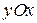 . и углом
. и углом 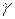 — между вектором
— между вектором 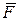 и его составляющей вдоль оси
и его составляющей вдоль оси 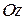 ; во втором случае (рис.2.13 б) положение вектора
; во втором случае (рис.2.13 б) положение вектора 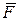 определяется тремя углами между направлением вектора
определяется тремя углами между направлением вектора 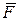 и положительными направлениями соответствующих осей:
и положительными направлениями соответствующих осей: 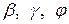 .
.

Рис.2.13 Проекции силы впространстве
Вначале разложим вектор 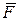 по двум направлениям
по двум направлениям 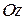 и
и 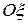 . Ось
. Ось 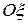 расположена в плоскости, проходящей через вектор силы
расположена в плоскости, проходящей через вектор силы 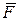 и ось Oz:
и ось Oz:
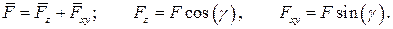
Вектор 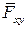 раскладывается по горизонтальным осям
раскладывается по горизонтальным осям 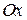 и
и 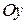 .
.
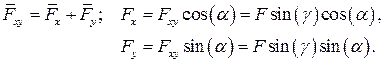
| Окончательно: | 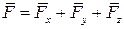
|
Последняя формула будет справедлива и при втором способе задания ориентации вектора 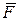 . В этом случае известны углы между вектором
. В этом случае известны углы между вектором 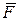 и направлением осей
и направлением осей 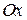 ;
; 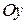 и
и 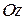 :
: 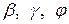 . По определению проекции силы на ось имеем
. По определению проекции силы на ось имеем
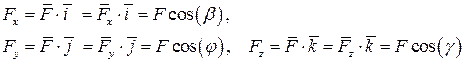
Введённые понятия позволяют перейти к условиям равновесия системы сходящихся сил.