
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Работа 3.
|
|
ОПРЕДЕЛЕНИЕ ДИСПЕРСИИ ДВУЛУЧЕПРЕЛОМЛЕНИЯ НЕМАТИЧЕСКОГО МОНОКРИСТАЛЛА.
Двулучепреломление кристаллических пластин, вырезанных вдоль оптической оси, обычно определяют с помощью компенсаторов, если ∆ п достаточно мало. Величину ∆ n можно определить способом канавчатого спектра, если дисперсия двулучепреломления ∆ n(λ) не слишком велика. В нематическом кристалле ∆ n(λ)=0, 2-0, 3 и ∆ n(λ) показывает сильную дисперсию. Поэтому для измерения ∆ n(λ) будем использовать метод канавчатого спектра со специальным способом расчёта ∆ п.
Нематический монокристалл получают натёртым в одном направлении стёклами ячейки. Оптическая ось совпадает с направлением директора n направлением натирания.
Метод канавчатого спектра основан на формуле пропускания (при скрещенных поляроидах):

Если оптическая ось образца повёрнута под углом 450 к направлению поляризации света, то
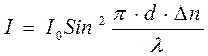
Ясно, что интенсивность пропущенного сквозь образец и скрещенные поляроиды света будет равна нулю при 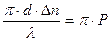 , где P=0, 1, 2, 3…
, где P=0, 1, 2, 3…
Образец является погашенным для длины волны λ, удовлетворяющем этому условию. Например, для изотропной среды или для одноосного кристалла, вырезанного перпендикулярно оптической -∆ n=0, и образец погашен при любых длинах волн.
Нематический кристалл, описанный ранее, гасится при строго
определенных длинах волн. Раскладывая белый свет, прошедший сквозь образец, в спектр, можно определить линии погасания.
Целью работы является определение длины волны по полосчатому спектру и расчёт дисперсии двулучепреломления ∆ n(λ) нематическог кристалла МББА. Спектр наблюдается с помощью спектральной насадки монохроматора УМ-2 (рис.1)
Зная градуировочную кривую монохроматора λ (N), можно получить зависимость m(λ), где m-номер линии погасания, начиная с первого в красной области спектра. График зависимости m(λ) используется для проверки точности измерения. Его точки должны лежать на гладкой кривой. Тангенс угла наклона кривой m(1/λ) даёт значения ∆ n для каждой пары точек.
Действительно,

Таким образом, полагая для каждой пары точек постоянным, получим ∆ n(λ i)d(1/λ i+1-1/λ)=1.
Тогда ∆ n(λ i) можно определить непосредственным расчётом
∆ n(λ i)=d-1(1/λ i+1-1/λ)-1.
| Номер лини m | λ | λ | 1/λ i+1-1/λ | ∆ n(λ i) |
| i=m |
Зависимость ∆ n(λ), полученная таким способом, даёт завышенные значения ∆ n. Это связано с большой дисперсией ∆ n(λ), особенно в области коротких длин волн, где нарушается условие ∆ n=const для соседних длин волн погасания. Более точные результаты можно получить следующим образом.
Предположим, что для участка с минимальной дисперсией (дальний “красный” участок спектра) величины ∆ n действительно не зависит от λ. Тогда можно определить ∆ n1 для двух соседних “красных” полос погасания по формуле:
(1/λ 2-1/λ 1) ∆ n1d=1
Зная ∆ n1, определим истинный номер линии погасания P1=∆ n1d/λ 1, отбрасывая десятые и сотые, составляя целую часть периода. Последующие номера линий погасания P2=P1+1, P3=P1+2 и т.д. Величины двулучепреломления для соответствующих длин волн определяются как
∆ n2= P2 λ 2/d; ∆ n3= P3 λ 3/d и т.д.
Таким образом, строится зависимость ∆ n(λ), более близкая к истинной, чем зависимость, определяемая по”тангенсу угла наклона”.
В работе требуется определить∆ n(λ) этими двумя способами.
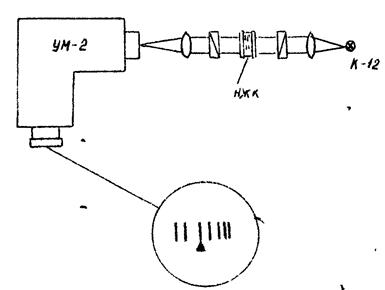
Рис.1 схема установки для получения канавчатого спектра.
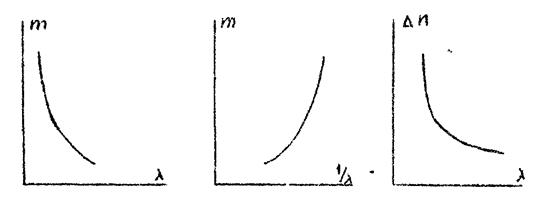
Рис.2 экспериментальные графики m(λ), m(1/λ) и ∆ n(λ).
Выполнение работы:
1.Провиреть положение поляроидов (скрещено) на установке с монохроматором УМ-2.
2. Поместить на столик образец с планарной текстурой (d=25мкм) МББА. Оптическая ось находится под углом 450 по отношению к направлениям поляризации.
3. 3. Получить канавчатый спектр поглощения. По шкале барабана монохроматора определить значения длин волн λ для полос погасания, начиная о красной части спектра. Градуировочный график монохроматора прилагается.
4.построить зависимости, описанные в работе ∆ n(λ) двумя методами расчёта: по тангенсу угла наклона, по “истинному” номеру линии погасания.
Вопросы:
1. Напишите формулу пропускания и определите условия погасания.
2. Опишите метод канавчатого спектра.
5. Почему второй способ расчёта даёт более точные значения ∆ n(λ).