Основные виды алгоритмов

Очевидно, что в зависимости от условий задач и исходных данных к ним алгоритмы решения этих задач будут различны. Однако можно выделить основные виды алгоритмов, используемых для решения простых задач. Эти простые алгоритмы и используются при составлении алгоритмов решения сложных задач. Основные виды простых алгоритмов будут пояснены ниже на соответствующих блок-схемах.

Линейный алгоритм

Алгоритм, в котором действия совершаются строго одно вслед за другим, называется ЛИНЕЙНЫМ.

Такими, например, будут алгоритмы вычислений по простейшим формулам: площадь круга, длина окружности, квадрат гипотенузы и т.д.

Для описания алгоритмов используют определенную форму записи - алгоритмический язык. Запись алгоритма должна оформляться по следующим правилам.

На первой строке записывается слово алгоритм или его трехбуквенное сокращение алг. Далее за этим словом записывается название алгоритма.

На второй строке записывается слово начало или его сокращение нач.

Далее в столбик записываются действия, составляющие алгоритм. Последней строкой описания алгоритма должно быть слово конец или кон. в той же позиции, что и слово начало. Общая форма записи:

алг. < название алгоритма>

нач. < составные команды>

действия

кон. < конец>

В алгоритмической форме можно записывать не только алгоритмы для вычислительных машин, но и различные инструкции, предписания и рекомендации для людей.

Например: инструкция по кипячению чайника в виде алгоритма, записанного на алгоритмическом языке и в виде блок-схем:

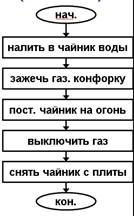
алг. < Кипячение чайника. >

нач.

налить в чайник воды

зажечь газовую конфорку

поставить чайник на огонь

когда чайник закипит, выключить газ

снять чайник с плиты

кон.

Следующий пример линейного алгоритма:

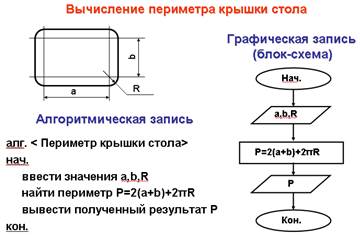
Алгоритмическая структура «ветвление»

Легко и просто было бы жить, если бы удалось раз и навсегда расписать какие поступки, и в какой последовательности совершать. На самом деле нам постоянно приходится принимать решения в зависимости от создавшейся ситуации. Если идет дождь, то мы берем зонт. Если жарко, то идем купаться. Разумеется, встречаются более сложные ситуации, когда надо делать выбор.

Логику принятия любого решения можно описать тремя ключевыми словами:

ЕСЛИ < условие> ТО < действия 1> ИНАЧЕ < действия2> - полная форма

Иногда < действия 2> могут отсутствовать:

ЕСЛИ < условие> ТО < действия 1> - неполная форма

Например:

ЕСЛИ хочешь быть здоров, ТО закаляйся, ИНАЧЕ валяйся весь день на диване

ЕСЛИ низко ласточки летают, ТО будет дождь, ИНАЧЕ дождя не будет

ЕСЛИ назвался груздем, ТО полезай в кузов.

Форма организации алгоритма действий, при которой в зависимости от выполнения некоторого условия совершается та или иная последовательность действий, называется ветвлением .

Для обозначений ветвлений на блок-схемах используются ромбы, называемые блоками проверки условия.

Рассмотрим два примера.

1. Алгоритм покупки билетов в кино может выглядеть так:

1) подойти к кассе

2) если билеты на сеанс 18.00 имеются, то купить билеты

3) отойти от кассы

2. Алгоритм вечера выходного дня. Тогда:

1) если уроки выучены, то иди гулять,

2) иначе учи уроки.

Мы видим, что при выполнении каждого из этих алгоритмов наступает такой момент, когда появляется несколько направлений для продолжения.

Алгоритм как бы раздваивается, разветвляется. В этом случае говорят, что алгоритм содержит ветвление.

Алгоритмическая запись ветвления:

Ветвление в неполной форме: Ветвление в полной форме:

если < условие> если < условие>

то серия 1 то серия 1

все иначе серия 2

все

Графическая форма записи (блок-схемы ветвления):

 

 

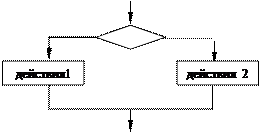Циклические алгоритмы

Вы легко заметите, что алгоритмы, которые мы составляли на предыдущих занятиях, обладают одним общим свойством: при их выполнении каждое действие совершается один раз или вообще не совершается. Однако человек постоянно встречается с ситуациями, для решения которых требуется многократно повторять одни и те же действия до тех пор, пока соблюдается некоторое заранее установленное условие. Используя только ветвление, такие алгоритмы не запишешь. Для этого нужна новая форма организации действий.

Предположим, нам необходимо письменно перевести английский текст на русский язык. Возможный алгоритм действий:

1) открыть текст;

2) прочесть предложение;

3) перевести это предложение на русский язык;

4) записать перевод в тетрадь;

{прочесть предложение; }

{перевести это предложение на русский язык; }

{записать перевод в тетрадь; }

5) если в тексте остались предложения, не переведенные на русский язык, то перейти к 1, в противном случае – завершить работу.

Ясно, что если мы соберемся писать этот алгоритм до конца, перевод придется отложить надолго.

Циклом (повтором) называется такая форма организации действий в алгоритме, при которой выполнение одной и той же последовательности команд повторяется до тех пор, пока истинно некоторое логическое выражение.

Циклический алгоритм – алгоритм, содержащий циклы.

Для организации цикла необходимо выполнить следующие действия:

· перед началом цикла задать начальное значение параметра;

· внутри цикла изменять параметр цикла с помощью оператора присваивания;

· проверять условие повторения или окончания цикла;

· управлять циклом, т.е. переходить к его началу, если он не закончен, или выходить из цикла в противном случае.

Ситуация, при которой выполнение цикла никогда не заканчивается, называется зацикливанием. Следует разрабатывать алгоритмы, не допускающие таких ситуаций.

Команда исполнителю многократно повторить указанную последовательность действий (тело цикла) называется командой повторения.

Различают следующие виды циклов:

Цикл с предусловием (цикл-пока), цикл с постусловием (цикл-до), цикл с параметром (цикл-для)

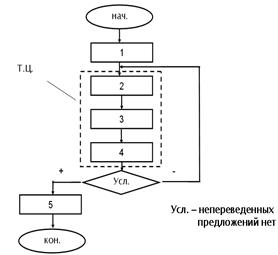
Составим блок-схему рассмотренного алгоритма: выделим последовательность действий, которые многократно повторяются при выполнении данного алгоритма. Очевидно, что это действия 2, 3 и 4. Последовательность этих действий называют телом цикла.

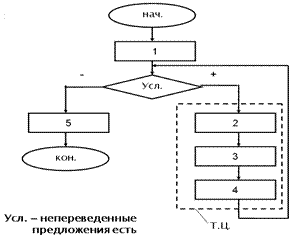
Проанализируем схему слева. Исполнитель сначала проверяет, выполняется ли условие. Если - да, то выполняется тело цикла, после чего условие проверяется снова, и т.д. Если же условие не выполняется, то исполнитель по ветви «нет» переходит к действию за пределом цикла.

Может случиться так, что условие не выполняется с самого начала (нет текста). Тогда действия, составляющие тело цикла, не совершаются ни разу.

Ту же самую работу можно описать и с помощью другого алгоритма. Набор действий будет тот же, однако порядок их выполнения будет иной.

Отличие данного алгоритма в том, что действия, составляющие тело цикла, сначала выполняются, и только потом проверяется условие. Оба эти алгоритма равноправны, но второй алгоритм имеет одно существенное отличие. При его выполнении, даже если условие сразу же не выполняется, тело цикла будет выполнено по крайне мере один раз. Это несущественное, на первый взгляд, отличие может иногда приводить к серьезным ошибкам. Предположим, что перевод текста будет поручена автомату, запрограммированному на выполнение второго алгоритма. Если окажется, что условие сразу не выполняется, то такой алгоритм не может быть исполнен, однако он предписывает перевести хотя бы одно предложение несуществующего текста: вряд ли автомат справится с решением этой простой задачи!

Для дальнейшей работы нам потребуется, чтобы выход из второго цикла осуществлялся по выходу «да».

Для этого, очевидно, проверяемое условие потребуется заменить на противоположное. Если в первом случае проверялось условие «непереведенные предложения есть?», то во втором случае проверяемое условие будет «непереведенных предложений нет?», или, в общем случае, если условие обозначим через P, то противоположное ему условие будет условие HE P. Кроме того, серию действий, составляющих тело цикла, обозначили в виде одного блока - т.ц. С учетом сказанного оба алгоритма (точнее, их циклическая часть), будут выглядеть следующим образом.

Алг.1 называется циклом с пред-условием (условие проверяется перед началом цикла) или циклом-пока.

Алг.2 называется циклом с пост-условием (условие проверяется после выполнения тела цикла) или циклом-до. В цикле-пока проверяемое условие является условием продолжения цикла. В цикле-до проверяемое условие есть условие выхода из цикла.

Задание на выполнение работы по переводу текста можно сформулировать и по-другому: перевести пять предложений, начиная с первого. В этом случае заранее известно число повторений. Такой цикл называют циклом-для, циклом с параметром, циклом со счетчиком.

Переменная k называется параметром (или счетчиком) цикла. Такой цикл оказывается весьма полезным при решении многих задач, поэтому важно рассмотреть его сокращенную форму записи:   ПЦ – параметр цикла НЗ – начальное значение параметра (1) КЗ – конечное значение параметра (5) Ш – шаг (1)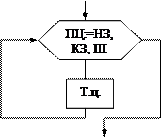

К циклическим алгоритмам сводится решение многих задач, как вычислительного, так и чисто практического характера. В качестве примеров рассмотрим задачи по сортировке шаров по цвету, на нахождение НОД двух чисел, а также нахождение суммы заданного числа первых членов числовой последовательности.

ПРИМЕР 1. В урне хранится некоторое количество черных и белых шаров. Требуется сделать запись алгоритма рассортировки этих шаров по двум корзинам (черного и белого цвета) так, чтобы в результате выполнения алгоритма белые шары оказались в белой корзине, черные – в черной.

Составим сначала схему алгоритма выполнения этой работы. Очевидно, что для рассортировки шаров по корзинам с каждым шаром должны быть проделаны следующие действия: вынуть шар из урны (в соответствии с условием задачи предполагаем, что урна с самого начала не пуста), определить цвет вынутого шара и опустить его в соответствующую корзину. Если после этого в урне еще остаются шары, описанные выше действия повторить еще раз и т.д. Схема искомого алгоритма изображена на рисунке. Можно заметить, что группа повторяющихся в цикле блоков образует довольно-таки сложную конструкцию, так как включает разветвление.

Пользуясь схемой, легко составить словесную запись этого алгоритма:

1. вынуть из урны один шар

2. если шар белый, идти к 4

3. опустить шар в черную корзину; идти к 5

4. опустить шар в белую корзину

5. если урна не пуста, идти к 1

6. конец.

ПРИМЕР 2. Составить алгоритм вычисления суммы первых 20 членов последовательности с общим членом a =k/(k² +1). Для циклического накопления сумм при составлении соответствующих алгоритмов используется предписание стандартного вида: сумма: =сумма+слагаемое.

Если повторить такое предписание требуемое количество раз, изменяя соответствующим образом слагаемое, то и будет получена искомая сумма. Понятно, что сумма перед началом работы цикла должна иметь нулевое значение. В схеме, изображенной на рисунке, роль суммы выполняет переменная S, а роль слагаемого - формула общего члена последовательности. Изменение слагаемого достигается увеличением в каждом обороте цикла номера члена k на единицу. Словесная запись этого алгоритма:

1.k: =1; S: =0

2.S: =S+k/(k^2+1)

В этом циклическом алгоритме управление окончанием цикла осуществляется проверкой условия k< =20, и производится эта проверка всегда после выполнения рабочей части цикла (см.рис.). Такие циклы называют циклами с пост-условием. Этот же алгоритм можно организовать иначе: поставить проверку окончания перед рабочей частью цикла. Такие циклы называют циклами с пред-условием. Ниже приведена словесная запись алгоритма, соответствующего схеме, изображенной на рисунке. При составлении предписания условного перехода оказалось удобнее взять не условие k< =20, а его отрицание k> 20.

В рамках рассмотренной задачи нахождения суммы 20 членов последовательности оба приведенных алгоритма равносильны в том смысле, что они дадут одинаковый результат. Впрочем, нужно отдавать себе отчет в том, что одинаковые по смыслу алгоритмы, составленные с пред-условием и пост-условием, все-таки различны. Очевидно, что рабочая часть (тело) циклов, построенных по схеме, всегда выполнится по меньшей мере один раз независимо от результатов проверки условия. В то же время тело цикла с пред-условием в определенной ситуации может не выполниться ни разу. Если допустить, что в задачах, подобно рассмотренной выше, верхняя граница параметра k заранее не известна и определяется, скажем, в результате предыдущего счета, то может оказаться, что алгоритм с пост-условием в этой ситуации даст нелепый результат. Действительно, если окажется, например, что заданная граница значения параметра k не положительна, то последовательность становится неопределенной. А алгоритм с пост-условием в этом случае выдаст в качестве значения суммы последовательности ее первый член.

Подобные ситуации требуют особого внимания при составлении программ, суммирующих последовательность.