Фільтри Баттерворта

Передавальна функція фільтра нижніх частот Баттерворта н-го порядку характеризується виразом фільтри Баттерворта

Передавальна функція фільтра нижніх частот Баттерворта н-го порядку характеризується виразом 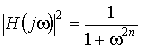. (7.1)

Амплітудно-частотна характеристика фільтра Баттерворта має такі властивості:

1. При будь-якому порядку n значення АЧХ .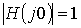

2. На частоті зрізу. .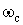

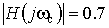АЧХ фільтра монотонно убуває з ростом частоти. З цієї причини фільтри Баттерворта називають фільтрами з максимально плоскими характеристиками. На рис. 15.4 показані графіки амплітудно-частотних характеристик фільтрів Баттерворта 3 і 5 порядків. Очевидно, що чим більше порядок фільтра, тим точніше апроксимується АЧХ ідеального фільтра нижніх частот.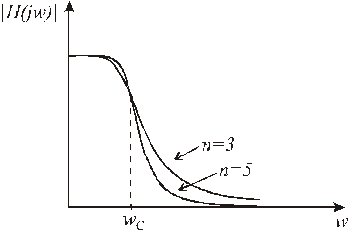

Рис. 7.1

Порядок передавальної функції п вибирають з умови забезпечення необхідного загасання в смузі затримання на частоті 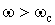. Модуль передавальної функції в смузі затримування

.

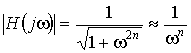Порядок передавальної функції визначається наближеною формулою 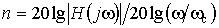. (7.2)

Тут 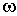– частота в смузі затримання, на якій задана величина загасання. Значення n, отримане за допомогою формули (15.5), округлюється до найближчого цілого, більшого n.

Приклад 7.1. Визначити порядок фільтра Баттерворта, у якого значення АЧХ на частоті,

рівної 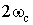, не перевищує 0.01.

Ріщення. В відповідн з (7.2) 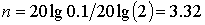. Округляючи до найближчого більшого цілого, отримуємо, що таке ослаблення в смузі затримання забезпечує фільтр Баттерворта четвертого порядку.

Визначаємо координати полюсів фільтра Баттерворта, вважаючи в (15.4) :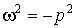

.

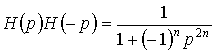Прирівнявши поліном знаменника нулю, знайдемо, що полюси фільтра Баттерворта з частотою зрізу 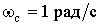розташовані на колі одиничного радіуса на однаковому кутовому відстані один від одного:

.

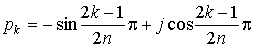Кожна пара комплексних спряжених полюсів утворює множник .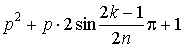

Фільтри Чебишева

Квадрат модуля передавальної функції фільтра Чебишева визначається виразом

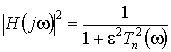. (7.3)

Тут 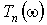- поліном Чебишева. Модуль передавальної функції фільтра Чебишева дорівнює одиниці на тих частотах, де 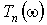звертається в нуль. Графік амплітудно-частотної характеристики фільтра Чебишева п'ятого порядку показаний на рис. 7.3.

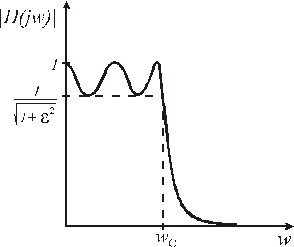
Рис. 7.3

Перерахуємо властивості частотних характеристик фільтрів Чебишева: В полосе пропускания АЧХ 1. 1. имеет равноволновой характер. На интервале 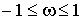имеется n точек, в которых функция 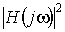достигает максимального значения, равного 1, или минимального значения, равного 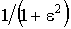. Если n нечетно, 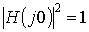, если n четно, .

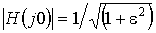2.Значение АЧХ фильтра Чебышева на частоте среза равно

.

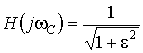3.При 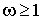функция 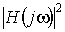монотонно убывает и стремится к нулю.

4, Параметр 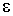определяет неравномерность АЧХ фильтра Чебышева в полосе пропускания:

.
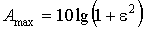