Краткое теоретическое введение

1. Индуктивность контура. Явление самоиндукции

Вокруг любого проводника с током I существует магнитное поле.

Собственное магнитное поле контура с током создает собственный магнитный поток 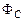через воображаемую поверхность S, ограниченную этим контуром,

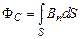, (15.1)

где 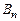– проекция вектора индукции 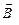магнитного поля тока I на нормаль к элементу поверхности dS.

Из закона Био–Савара–Лапласа и принципа суперпозиции следует, что эта проекция при постоянном значении магнитной проницаемос-
ти m равна

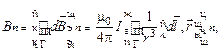
где 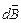– вектор индукции магнитного поля, созданного элементом замкнутого контура Гс током I в точке, местоположение которой относительно определяется радиус – вектором .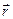

Подставляя выражение для 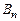в формулу (15.1) и вынося из-под знака интеграла постоянные, получаем

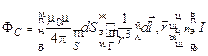(15.2)

или

.

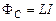Коэффициент пропорциональности между собственным потоком вектора магнитной индукции 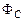через поверхность, ограниченную контуром, и силой тока в этом контуре называется индуктивностью контура (коэффициентом самоиндукции).

Из формулы (15.2) следует, что индуктивность контура зависит только от геометрических размеров, формы контура и магнитной проницаемости 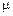той среды, в которой он находится.

Единица индуктивности в СИ называется Генри (Г):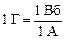

Для достаточно длинного соленоида, витки которого плотно прилегают друг к другу и сделаны из проводника с очень малым поперечным сечением, индуктивность выражается следующей формулой:

, (15.3)

где 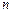– плотность намотки витков соленоида; 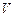– объем соленоида;
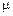– магнитная проницаемость вещества сердечника.

Если сила тока, протекающего по контуру, изменяется со временем, то в соответствии с законом Фарадея в контуре наводится ЭДС самоиндукции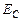

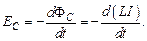
Если контур с током не деформируется и магнитная проницаемость среды 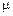не изменяется (нет ферромагнетиков в магнитном поле контура), то и

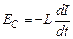. (15.4)

По правилу Ленца, ЭДС самоиндукции противодействует изменению тока в контуре, замедляя как его возрастание, так и убывание.

2. Закон изменения тока в цепи при подключении

и отключении источника.

Применение закона для определения индуктивности

Найдем изменение тока в цепи, состоящей из последовательно соединенных соленоида, индуктивность которой равна , и резистора, активное сопротивление которого .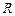

Если внешнее магнитное поле отсутствует или постоянно, а контур неподвижен, то индукционные явления обусловлены только самоиндукцией.

Из закона Ома для замкнутой цепи, в которой действует источник ЭДС , а общее активное сопротивление 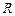, сила тока равна

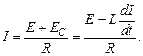
Для нахождения зависимости силы тока от времени разделим переменные

.

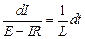Полагая постоянными и интегрируя, получаем

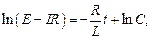
где 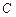– постоянная интегрирования, значение которой определяется начальными условиями решаемой задачи.

Пусть в момент времени 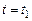сила тока 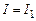. Тогда

Выразив силу тока, получим

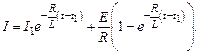(15.5)

Из этой общей формулы можно получить зависимость силы тока от времени при замыкании цепи. В этом случае начальный ток равен нулю 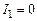и выражение (15.5) приобретает вид

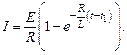(15.6)

Из этой формулы видно, что сила тока при замыкании цепи постепенно увеличивается, стремясь к 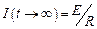, соответствующей величине постоянного тока (рис. 15.1). Нарастание тока происходит тем медленнее, чем меньше отношение 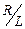в показателе степени экспоненты или больше обратное отношение , физический смысл которого обсуждается ниже.

Если же в момент времени 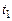при силе тока 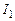источник ЭДС отключить (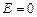), сохранив замкнутость цепи, то из формулы (15.5), получим следующую зависимость силы тока от времени:

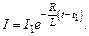(15.7)

В этом случае сила тока в цепи постепенно уменьшается от начального значения 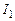, стремясь к нулю. При этом за время (время релаксации) сила тока изменяется в 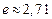раза.

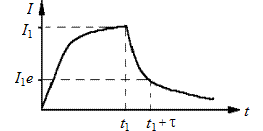
Рис. 15.1

Следует заметить, что в опыте удобнее снимать вместо зависимости силы тока в цепи от времени 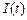зависимость напряжения на некотором известном активном сопротивлении , последовательно включенном в цепь, от времени . Напряжение в этом случае будет пропорционально силе тока.

Из сказанного ясно, что, измерив силу токов (или напряжения) в некоторые моменты времени 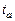, и зная, кроме того, величину общего активного сопротивления контура 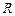, можно с помощью зависимостей (15.6) или (15.7) определить индуктивность контура .

Особенно просто, зная активное сопротивление цепи 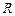, определить её индуктивность, измерив время релаксации,

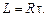(15.8)

3. Вынужденные электромагнитные колебания в контуре,

их применение для измерения индуктивности

Рассмотрим контур, состоящий из последовательно соединенных конденсатора емкостью 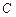, активного сопротивления 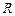и соленоида индуктивностью .

Для получения незатухающих электромагнитных колебаний необходимо включить в контур источник тока с периодически изменяющейся ЭДС (рис. 15.2).

Рис. 15.2

В этом случае колебания в контуре являются вынужденными.

Пусть внешняя ЭДС изменяется по гармоническому закону

.

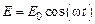Тогда, используя закон Ома, можно получить следующее дифференциальное уравнение вынужденных электромагнитных колебаний

и, решив это уравнение, найти для установившихся вынужденных колебаний связь амплитудных значений силы тока и внешней ЭДС

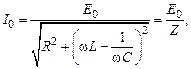(15.9)

где величина называется полным сопротивлением электрической цепи переменного тока.

В нее входят активное сопротивление 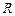контура, емкостное сопротивление и индуктивное сопротивление .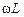

Если электрическая емкость контура стремится к бесконечности 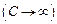, то есть емкостное сопротивление к нулю, то формула (15.9) упрощается

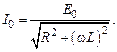(15.10)

Используя это выражение, получаем рабочую формулу для экспериментального определения индуктивности соленоида. При этом учтем, что амплитуда падения напряжения на активном сопротивлении R связана с амплитудой силы тока в цепи формулой

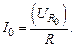(15.11)

Из выражений (15.10) и (15.11) получим

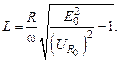(15.12)