Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Плотность распределения вероятностей. Интегральная функция распределения НСВХ.
|
|
ЛЕКЦИЯ 12
ТЕМА: НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
Плотность распределения вероятностей. Интегральная функция распределения НСВХ.
Напомним определение непрерывной случайной величины:
Непрерывной случайной величиной (НСВ) называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Множество возможных значений непрерывной случайной величины бесконечно и несчетно.
Диаметр изготавливаемой детали на станке - непрерывная случайная величина, т.к. возможны отклонения из-за возникающих погрешностей ввиду температурных изменений, силы трения, неоднородности материала и т.д., а диаметр может принять любое значение из промежутка (c, d).
Непрерывную случайную величину, так же как и ДСВ, можно задать с помощью функции распределения, которая равна вероятности того, что СВХ приняла значение меньшее заданного х. Для вывода формулы функции распределения НСВХ познакомимся сначала с плотностью распределения вероятностей НСВХ.
Введем ограничение: рассмотрим только такие СВХ, для которых вероятность попадания в интервал (х; х+Dх), где Dх> 0 и Dх®0, пропорциональна длине интервала Dх, т.е. Р(х, х+Dх)» р(х)Dх, где р(х)- коэффициент пропорциональности, р(х) Dх- элемент вероятности. Выясним его смысл с помощью полученного приближенного равенства:

Следовательно, р(х) - есть вероятность, которая приходится на единицу длины, рассматриваемого участка и равна производной интегральной функции распределения. Поэтому р(х) называют плотностью распределения вероятностей или дифференциальной функцией распределения.
Если все значения НСВХ принадлежат некоторому интервалу (а; в), то интегральная функция распределения имеет вид:
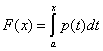
Если НСВХ может принять любое действительное значение, то функция имеет вид:
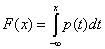
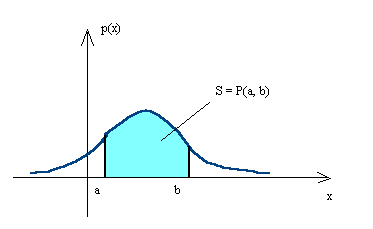
Вероятность попадания НСВХ в некоторый интервал (a, b) равна:
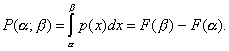
Из геометрического смысла определенного интеграла следует, что вероятность попадания НСВХ в заданный интервал равна площади криволинейной трапеции, ограниченной осью абсцисс, прямыми х=а и х=b графиком функции р(х), который называется кривой распределения вероятностей.
Т.к. в результате опыта случайная величина обязательно примет какое-либо из возможных значений, то:
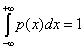
или