
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Онтогенетические колебания биологического времени растений: яровые и озимые формы
|
|
На основе теории колебаний предложена единая динамическая модель роста общей сухой биомассы, процессов фотосинтеза и дыхания растений для озимых и яровых форм. Учитываются критические температуры вымерзания озимых, минимальные, оптимальные и максимальные значения факторов внешней среды: прихода ФАР, температуры воздуха, влажности почвы. Основное различие яровых и озимых форм растений обеспечивается начальной фазой колебаний устойчивой составляющей логистической кривой роста общей сухой биомассы растений в онтогенезе.
Ключевые слова: рост, развитие, фотосинтез, дыхание, логистическая кривая, время, онтогенез, перезимовка, факторы среды.
Введение. Вопрос о перезимовке озимых культурных растений и их контроль (пшеницы, рожь, ячмень) разрабатывался агрометеорологами [1 - 10], физиологами растений [11], морфофизиологами [12, 13]. Такие исследования, начатые в XX веке [5], продолжаются до настоящего времени [7, 8, 9, 10]. В первую очередь были собраны данные, характеризующие состояние условий внешней среды (агрометеорологические факторы) и состояние зимующих растений, как на момент зимнего периода, так и на момент завершения зимнего периода – состояние озимых культур на начало весеннего периода жизни в зависимости от агрометеорологических условий перезимовки. При этом, в литературе, рассматриваются условия осеннего периода вегетации и их состояние в период перезимовки. Прежде всего, рассматриваются условия закалки растений, их жизнестойкость к неблагоприятным факторам внешней среды. Рассматриваются вопросы о величине накопления сахаров в озимом растении к моменту ухода в зиму и требования озимых к минимальному состоянию факторов внешней среды, прежде всего к минимальной температуре почвы на глубине узла кущения, которую способна выдержать озимая культура в период зимы. Согласно новейшим исследованиям В.С. Антоненко [7, 8, 9, 10] предложены динамические модели роста, развития и формирования урожая озимой пшеницы и в том числе динамический блок модели «перезимовка», в котором рассматривается динамический процесс накопления сахаров, их расход, и состояние зимующих растений в зимний период в зависимости от состояния агрометеорологических факторов внешней среды. При этом, весь онтогенез озимых форм культурных растений (на примере озимой пшеницы) разбивается на следующие отдельные периоды [7]: 1. Период прорастания семян; 2. Период осенней вегетации; 3. Период перезимовки; 4. Период весенне-летней вегетации. Как мы понимаем, для каждого периода, в неявной форме (моделируемой – расчетной) существует своя логистическая кривая. В то же время цельной логистической кривой для озимых культур нет. Предложены лишь логистические кривые для теплого времени года – весенне-летнего периода вегетации, или что, то же, для яровых культур [14]. Отметим так же и то, что Д.А. Сабинин, по данным [14], уделял большое внимание поиску определенного вида логистической кривой роста растений. Кроме того, как для озимых, так и для яровых физиологические процессы идут на протяжении всего онтогенеза. В данной работе мы рассмотрим вопрос о различии видов логистической кривой для яровых и озимых форм на основе теории колебаний биологического времени растений в онтогенезе [15, 16]. В основе такой теории лежат три уравнения:
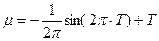 ; (1)
; (1)
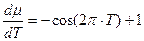 ; (2)
; (2)
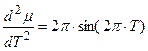 , (3)
, (3)
где заключительное дифференциальное уравнение колебаний имеет вид
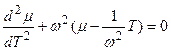 , (4)
, (4)
где μ – устойчивая составляющая роста растений – нормированная логистическая кривая, изменяется от 0 до 1; Т – весь онтогенез роста растений, нормированная временная величина, изменяется от 0 до 1; ω – период колебаний нормированной сухой биомассы всего организма растения в онтогенезе. Уравнения (1 – 4) выражают колебательный характер движений нормированной сухой биомассы растений в течение онтогенеза, то есть за период ω. Мы считаем, что, и биологическое время растений так же имеет колебательный характер движения в онтогенезе (см. так же [17, 18, 19])
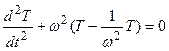 , (5)
, (5)
где t – календарное или физическое время.
Материалы и методы исследования. Согласно теории колебаний [17, 18, 19], запишем уравнения колебаний (1 – 3) с необходимой начальной фазой колебаний Q 0
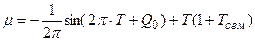 ; (6)
; (6)
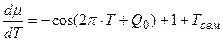 ; (7)
; (7)
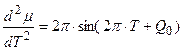 , (8)
, (8)
где Q 0 – начальная фаза колебаний биологического времени в онтогенезе растений, изменяется в радианах от начального значения до 2π, константа; Тсем – биологическое время семян, отн. ед., константа.
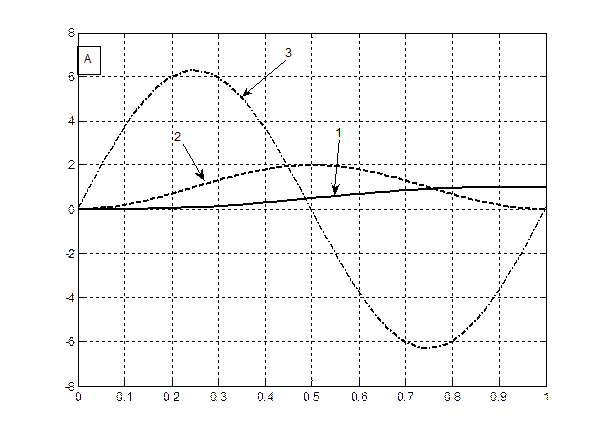
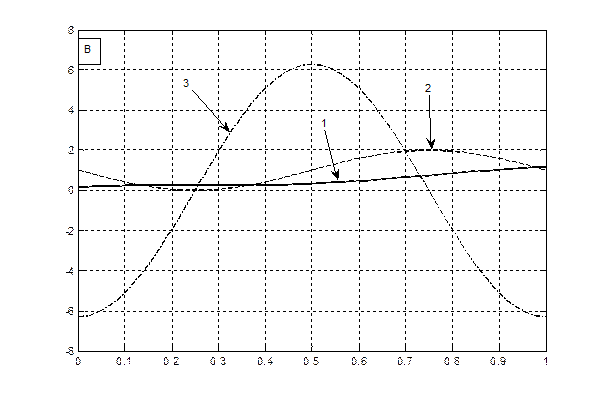
Теперь нам осталось построить графики всех трех уравнений (6 – 8) на одном и том же рисунке для их сопоставления, для яровых (рис. 1 – А) и озимых форм (рис. 1 – B). При чтении рисунков необходимо отметить, что уравнение (6) – это устойчивая составляющая нормированной сухой биомассы роста растения, поэтому единицы измерения этого уравнения – нормированные граммы сухого вещества общей биомассы растения. Уравнение (7) – это скорость нормированного значения процесса фотосинтеза всего организма растения, согласно известному уравнению Давидсона и Филиппа [20], то есть скорость газообмена растения. Единицы измерения этого уравнения – нормированные граммы сухого вещества в единицу времени. Что касается уравнения (8), то это уравнение выражает характеристику процесса дыхания всего организма растения в онтогенезе. При этом, как мы видим, это не первая, как в уравнении процесса фотосинтеза (7), а вторая производная по переменной времени. В то же время, существующие методы измерения дыхания растения или его отдельных органов характеризуют этот процесс в единицах измерения грамм сухого вещества в единицу времени [21, 22]. То есть, получается, что мы вторую производную (дыхание)
μ, dμ /dT, d2μ /dT2
Т
Рис. 1 – Характеристики устойчивых составляющих процессов: роста – 1, фотосинтеза – 2, дыхания – 3, для яровых (А) и озимых форм (B) согласно теории колебаний (Q 0 = 0.01 π – график А; Q 0 = 1.501 π – график B).
измеряем интегральным показателем. Поэтому здесь, впервые получена дифференциальная оценка процесса дыхания, его устойчивая составляющая в онтогенезе растения, не зависящая от агрометеорологических условий.
Теперь рассмотрим графики яровых, рис. 1 А, и озимых форм, рис. 1 B. Как видно из данных, представленных на рис. 1 А, дифференциальная характеристика дыхания в нулевой точке онтогенеза (Т =0) отлична от нуля. То есть семена растений всегда дышат. Это зафиксировано в экспериментальных наблюдениях. В то же время, на рис. 1 А и рис. 1 B наблюдается сдвиг начальной фазы движения (колебания) дифференциальных процессов дыхания для яровых - рис. 1 А, и озимых форм - рис. 1 B. Кроме того, для процесса фотосинтеза, кривые 2 на рис. 1, мы видим, что для яровых форм культурных растений скорость процесса фотосинтеза постепенно увеличивается, доходит до максимума и, затем снижается, в силу процессов старения организма растения. Точнее процессы старения организма растения для яровых форм культурных растений, очевидно, вызваны общим процессом колебаний биологического времени в онтогенезе, когда отталкиваясь от центрального процесса в растении – цветения, происходят колебания биологического времени: от состояния равновесия -«семена до посева», затем в момент цветения – максимальная скорость онтогенетического движения биологического времени и заканчивается такое колебание опять состоянием равновесия – «созревшие семена». В целом мы видим, что интегральный процесс – устойчивая составляющая роста μ (уравнение (6)) подчиняется сигмоидному закону роста, как для яровых, так и для озимых форм растений [23].
Отметим так же и то, что дифференциальная характеристика процесса дыхания в онтогенезе, как для яровых, так и для озимых форм культурных растений никогда не бывает постоянной величиной – она всегда изменяется по отношению к оси времени. То есть процесс дыхания происходит в растении как в весеннее-летний период, так и в период перезимовки. То же самое можно отметить и для процесса фотосинтеза, только следует учитывать его скорость прохождения или интенсивность. Так, в период перезимовки, скорость процесса фотосинтеза является минимальной. Этот анализ целиком и полностью касается устойчивых составляющих роста, фотосинтеза и дыхания растений, не зависящих от погодных, агрометеорологических условий.
Результаты исследования и их анализ. Теперь представим динамическую модель роста общей биомассы культурных растений, как яровых, так и озимых форм. Отличие яровых от озимых характеризуется только лишь параметрами такой модели.
Развитие. Для начала расчетов необходимо определить биологическую ось времени, которая бы выражала возраст растений и по отношению к которой, мы могли бы определять интересующие нас процессы, проходящие в онтогенезе растений. Для этого мы воспользуемся следующим уравнением [24, 25], состоящим из двух кусков:
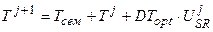 , Тсем < T ≤ 0.5; (9)
, Тсем < T ≤ 0.5; (9)
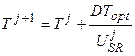 , 0.5 ≤ T ≤ 1, (10)
, 0.5 ≤ T ≤ 1, (10)
где Т – биологическая ось времени, изменяется от некоторого Тсем до 1, отн. ед. биологического времени, где весь онтогенез составляет одну единицу биологического времени; Тсем – биологическое время семян, отн. ед. биологического времени; DТopt – константа, максимальная скорость развития, отн. ед. биологического времени∙ сут-1; USR – уровень напряженности факторов внешней среды, изменяется от нуля (нулевая биологическая активность) до единицы (оптимальная биологическая активность), отн. ед.; j – номер суток расчетного периода.
Определив, таким образом, биологическую ось времени, мы теперь можем по отношению к ней рассматривать процессы роста растений.
Рост растений. Для описания роста общей сухой биомассы растений в зависимости от агрометеорологических условий в качестве основы, мы будем использовать устойчивую составляющую скорости процесса фотосинтеза растений (уравнение (7))
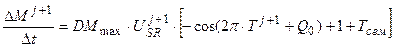 , (11)
, (11)
где Δ M/Δ t – реальная скорость роста общей, сухой биомассы посева растений, гс.в.·м-2·сут-1; DMmax – максимальная скорость роста общей, сухой биомассы посева растений в оптимальных условиях внешней среды, гс.в.·м-2·сут-1.
Уровень напряженности агрометеорологических факторов. В первом приближении, мы будем рассматривать факторы света, тепла и влаги. При этом, при построении взаимосвязей мы воспользуемся фундаментальным принципом Либиха-Блекмана, который говорит о том, что фактор находящийся в минимуме определяет продуктивность роста растений:
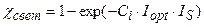 ; (12)
; (12)
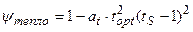 ; (13)
; (13)
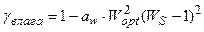 , (14)
, (14)
где χ свет – нормированная световая кривая скорости фотосинтеза культуры, отн. ед; Iopt – оптимальный поток ФАР на верхней границе посева для прохождения процесса фотосинтеза с максимальной скоростью, Вт·м-2; IS – нормированный, реальный поток ФАР на верхней границе посева, отн. ед; Ci – параметр световой кривой, вместе с величиной Iopt определяет степень изгиба световой кривой, м-2·Вт-1; ψ тепло – нормированная температурная кривая фотосинтеза культуры, отн. ед; topt – оптимальная температура воздуха для прохождения процесса фотосинтеза культуры, оС; tS – нормированная, реальная температура воздуха внутри посева, отн. ед; at – параметр температурной кривой, наряду с величиной topt определяет критические точки прохождения процесса фотосинтеза: минимальную (критическую температуру вымерзания озимых), оптимальную и максимальную температуру воздуха для фотосинтеза, оС-2; γ влага – нормированная влажностная кривая фотосинтеза культуры, отн. ед; Wopt – оптимальные запасы продуктивной влаги в корнеобитаемом слое почвы для прохождения процесса фотосинтеза, мм; WS – нормированные, реальные запасы продуктивной влаги в корнеобитаемом слое почвы, отн. ед; aw – параметр влажностной кривой фотосинтеза культуры, наряду с величиной Wopt определяет критические точки прохождения процесса фотосинтеза: минимальные, оптимальные и максимальные запасы продуктивной влаги в почве, мм-2.
Для расчета потока ФАР на верхней границе посева используется стандартное уравнение С.И. Сивкова [26, 27]
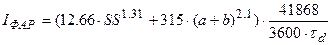 , (15)
, (15)
где IФАР – поток ФАР на верхней границе посева, Вт·м-2; SS – продолжительность солнечного сияния в сутки, ч; a+b = sinh 0 – где: h 0 – полуденная высота Солнца; τ d – длина светлого времени суток, ч.
Нам остается найти реальные, нормированные значения потока ФАР, температуры воздуха и запасов продуктивной влаги в корнеобитаемом слое почвы:
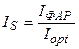 ;
; 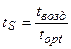 ;
; 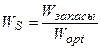 . (16)
. (16)
где tвозд – текущая температура воздуха, оС; Wзапасы – текущие запасы продуктивной влаги в корнеобитаемом слое почвы, мм.
Окончательно, уровень напряженности факторов внешней среды находится мультипликативным образом, где учтено влияние каждого фактора на скорость прохождения процесса фотосинтеза культуры
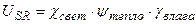 . (17)
. (17)
Параметры модели для озимых и яровых форм растений. Мы рассмотрим различие параметров представленной модели на примере ярового ячменя (сорт «Одесский 115») и озимой пшеницы (сорт «Мироновская 61»), выращиваемых в условиях Киевской области ст. Мироновка в агрометеорологических условиях вегетации 1993 года. Посев ярового ячменя был произведен 22.04.1993 г., всходы появились 02.05.1993 г., цветение ярового ячменя наблюдалось 06.07.1993 г., полное созревание наблюдалось 02.08.1993 г. Весь вегетационный период (онтогенез), от посева до полного созревания ярового ячменя составил 102 суток вегетации. Посев озимой пшеницы был произведен 24.09.1992 г., всходы озимой пшеницы появились 08.10.1992 г., прекращение осенней вегетации наблюдалось 21.11.1992 г., возобновление вегетации наблюдалось 28.04.1993 г., цветение озимой пшеницы наблюдалось 18.06.1993 г., полная спелость наблюдалась 26.07.1993 г. Весь вегетационный период озимой пшеницы (онтогенез), от посева до полной спелости (включая перезимовку), составил 305 суток. Параметры динамической модели накопления общей сухой биомассы таких двух культур, как яровой ячмень и озимая пшеница представлены в табл. 1.
Таблица 1 – Параметры динамической модели роста общей сухой биомассы посева, для озимых и яровых форм культурных растений на примере ярового ячменя и озимой пшеницы
| Культура | DTopt | DMmax | Q0 | Ci | at | aw | Iopt | topt | Wopt |
| Озимая пшеница | 0.0044 | 4.70 | 1.51π | 0.01 | 0.00077 | 0.000031 | 18.0 | ||
| Яровой ячмень | 0.0098 | 7.50 | 0.01π | 0.01 | 0.00175 | 0.000040 | 18.0 |
Примечание к таблице: DТopt – константа, максимальная скорость развития, отн. ед. биологического времени∙ сут-1; DMmax – максимальная скорость роста общей, сухой биомассы посева растений в оптимальных условиях внешней среды, гс.в.·м-2·сут-1; Q0 – начальная фаза колебаний биологического времени в онтогенезе растений, изменяется в радианах от начального значения до 2π, константа; Ci – параметр световой кривой, вместе с величиной Iopt определяет степень изгиба световой кривой, м-2·Вт-1; at – параметр температурной кривой, наряду с величиной topt определяет критические точки прохождения процесса фотосинтеза: минимальную (критическую температуру вымерзания озимых), оптимальную и максимальную температуру воздуха для фотосинтеза, оС-2; aw – параметр влажностной кривой фотосинтеза культуры, наряду с величиной Wopt определяет критические точки прохождения процесса фотосинтеза: минимальные, оптимальные и максимальные запасы продуктивной влаги в почве, мм-2; Iopt – оптимальный поток ФАР на верхней границе посева для прохождения процесса фотосинтеза с максимальной скоростью, Вт·м-2; topt – оптимальная температура воздуха для прохождения процесса фотосинтеза культуры, оС; Wopt – оптимальные запасы продуктивной влаги в корнеобитаемом слое почвы для прохождения процесса фотосинтеза, мм;
Опираясь на эти параметры (табл. 1), были проведены расчеты на ЭВМ с учетом агрометеорологических данных вегетации озимой пшеницы и ярового ячменя 1993 года. При расчетах бралась среднедекадная температура воздуха, запасы продуктивной влаги в метровом слое почвы, среднедекадное число часов солнечного сияния в период онтогенеза. Результаты расчетов представлены на рис. 2 и рис. 3.
Δ М/Δ t, гс.в.·м-2·сут-1
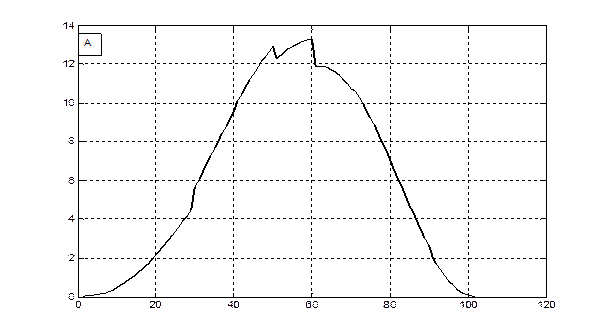
сутки от посева
М, гс.в.·м-2
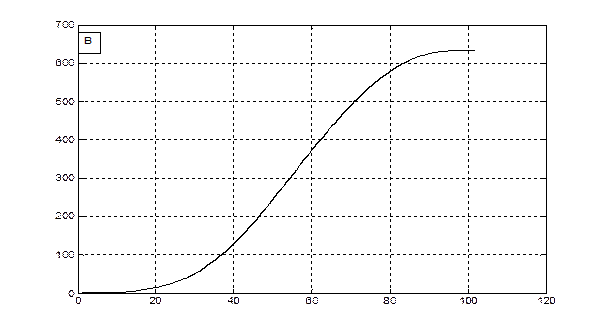
сутки от посева
Рис. 2 – Скорость фотосинтеза (А) и рост общей сухой биомассы (B) посева ярового ячменя в агрометеорологических условиях вегетации 1993 года.
Δ М/Δ t, гс.в.·м-2·сут-1
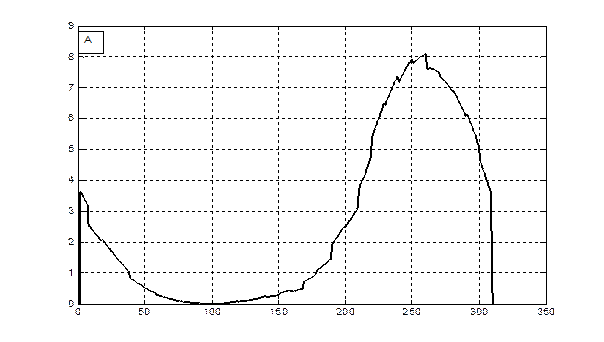
Сутки от посева
М, гс.в.·м-2
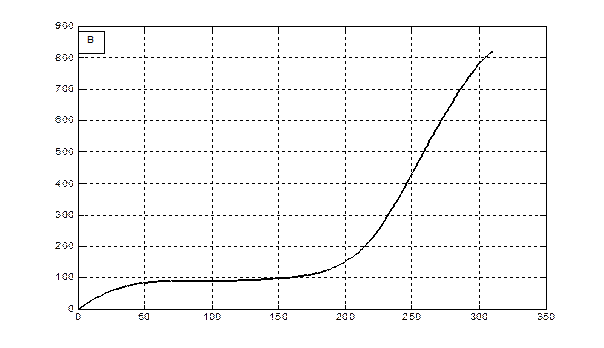
Сутки от посева
Рис. 3 - Скорость фотосинтеза (А) и рост общей сухой биомассы (B) посева озимой пшеницы в агрометеорологических условиях вегетации 1992 - 1993 года.
Отметим, что как для яровых культур, так и для озимых культур данная модель интегрирует всю сухую биомассу, которая образуется в процессе роста растений, с учетом отмирающих частей растения в процессе старения или в процессе перезимовки. Процесс старения и отмирания отдельных частей растения не рассматривается. В этом смысле мы получаем всю продуцируемую сухую биомассу, которая образуется в процессе фотосинтеза. Именно поэтому для озимых (рис. 3 В) отрастание весной, на 150-е сутки от посева, началось со значений общей сухой биомассы в 100 гс.в.· м-2.
Выводы. Таким образом, проведенные расчеты по двум культурам (яровой ячмень и озимая пшеница) убедительно показали и подтвердили правильность выбранной, устойчивой составляющей логистической кривой роста растений, где яровые и озимые формы отличаются начальной фазой колебаний во всем онтогенезе. Нормированные кривые света, тепла, влаги обеспечивают подбор параметров с учетом критических значений вымерзания озимых, минимальных, оптимальных и максимальных значений температуры воздуха, влажности почвы, прихода ФАР для прохождения процесса фотосинтеза, дыхания и общего роста растений. Дальнейшее развитие предложенного подхода к предложенным расчетам может заключаться во включении в данную модель функций распределения ассимилятов, которые позволят вести динамический расчет роста отдельных органов растений, их отмирание, включая перезимовку и учитывать повреждения растений от низких температур.
Список литературы
- Моисейчик В.А. Агрометеорологические условия и перезимовка озимых культур. – Ленинград: Гидрометеоиздат, 1975. – 295 с.
- Палагин Э.Г. Математическое моделирование агрометеорологических условий перезимовки озимых культур. – Ленинград: Гидрометеоиздат, 1981. – 191 с.
- Личикаки В.М. Перезимовка озимых культур. – Москва: «Колос», 1974. – 207 с.
- Коровин А.И. Растения и экстремальные температуры. – Ленинград: Гидрометеоиздат, 1984. – 271 с.
- Петунин И.М. К вопросу вымерзания озимых посевов пшеницы и ржи // Труды ЦИП. – 1949. - Вып. 18(45). – С. 36 – 37.
- Уланова Е.С. Агрометеорологические условия и урожайность озимой пшеницы. – Ленинград: Гидрометеоиздат, 1975. – 302 с.
- Антоненко В.С. Научно-методические основы идентификации параметров модели влияния агрометеорологических условий на рост, развитие и формирование урожая озимой пшеницы // Метеорологія, кліматологія та гідрологія. - 2001. - Вип. 43. – С. 98 – 105.
- Антоненко В.С. Моделирование влияния агрометеорологических условий на процесс закаливания и перезимовку озимой пшеницы // Український гідрометеорологічний журнал. – 2006. - №1. – С. 95 – 103.
- Антоненко В.С. Моделирование влияния агрометеорологических условий на процесс прорастания семян озимой пшеницы // Український гідрометеорологічний журнал. – 2009. - №5. – С. 158 – 162.
- Антоненко В.С. Моделирование осенней вегетации озимой пшеницы // Вісник ОДЕКУ. – 2009. – Вип. 8. – С. 133 – 139.
- Туманов И.И. Физиология закаливания и морозостойкость растений. – Москва: «Наука», 1978. – 350 с.
- Куперман Ф.М., Ржанова Е.И. Биология развития растений. – Москва: «Высшая школа», 1963. – 450 с.
- Куперман Ф.М., Моисейчик В.А. Методическое пособие. Оценка состояния озимых зерновых культур методом биологического контроля в осенний, зимний и весенний периоды. – Москва: Московское отделение Гидрометеоиздата, 1977. – 24 с.
- Обручева Н.В., Ковалёв А.Г. О физиологической интерпретации сигмоидных кривых роста органов растений // Физиология растений. – 1979. – Т. 26. – Вып. 5. – С. 1029 – 1043.
- Наумов М.М. Модель роста общей биомассы сельскохозяйственных культур, построенная на основе логистической кривой // Вісник ОДЕКУ. – 2010. – Вип. 9. – С. 63 – 72.
- Наумов М.М. Простая модель развития и роста сельскохозяйственных культур // Вестник Гидрометцентра Черного и Азовского морей. – 2009. - № 2[10], Декабрь 2009 г. – С. 218 – 227.
- Самойленко А.М., Кривошея С.А., Перестюк Н.А. Дифференциальные уравнения: примеры и задачи. – Москва: «Высшая школа», 1989. – 383 с.
- Крауфорд Ф. Волны. – Москва: «Наука», 1984. – 511 с.
- Стрелков С.П. Введение в теорию колебаний. – Москва: «Наука», 1964. – 437 с.
- Davidson J.L. Phillip J.R. Light and pasture growth // In.: Climatology and Microclimatology. - UNESCO. – 1958. – P. 181 – 187.
- Фотосинтез, продукционный процесс и продуктивность растений. – Киев: «Наукова Думка», 1989. – 152 с.
- Голик К.Н. Темновое дыхание растений. – Киев: «Наукова Думка», 1990. – 136 с.
- Синнот Э. Морфогенез растений. – Москва: Из-во иностранной литературы, 1963. – 603 с.
- Наумов М.М. Рост растений и биологическое время // Вісник ОДЕКУ. – 2005. – Вип. 1. – С. 72 – 78.
- Наумов М.М. Рост растений и биологическое время. Результаты расчетов // Вісник ОДЕКУ. – 2006. – Вип. 2. – С. 101 – 107.
- Полевой А.Н. Теория и расчет продуктивности сельскохозяйственных культур. – Ленинград: Гидрометеоиздат, 1983. – 175 с.
- Сиротенко О.Д. Математическое моделирование вводно-теплового режима и продуктивности агроэкосистем. – Ленинград: Гидрометеоиздат, 1981. – 167 с.
|