
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Распределение молекул по энергиям
|
|
| Рис. 6.5 Распределение молекул по энергии |
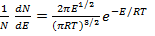 (6.7)
(6.7)
которое показывает количество молекул, обладающих энергией от Е – dE до Е + dE В графической форме это распределение показано на рис. 6.5. Уравнение 6.7. является дифференциальным. Более общий случай, для больших интервалов энергий, описывается распределением Больцмана в интегральном виде:
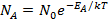 (6.7.1)
(6.7.1)
здесь NA – число молекул с энергией ЕA, N0 – общее число молекул, k = R/Na – константа Больцмана, равная отношению газовой постоянной и числа Авагадро.
На рисунке 6.5 приведены две кривые распределения, расчитанные для разных температур. Максимумы на каждой кривой соответствуют средней энергии (ось Х) и наибольшему числу молекул (ось Y). Эта средняя энергия при повышении температуры незначительно смещается в область высоких энергий, и в дальнейшем будем считать (для небольшого интервала температур) ее постоянной. Молекулы, обладающие средней энергией, при соударении не способны прореагировать друг с другом, для этого необходима более высокая энергия, которую обозначим Е*. Все частицы, имеющие энергию > Е* будут вступать в реакцию, для определения этого значения введем понятие энергии активации ЕA.