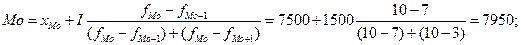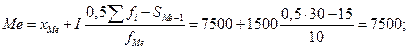Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Краткие методические указания к решению задачи 7
|
|
Величины моды  и медианы
и медианы  рассчитаем по формулам:
рассчитаем по формулам:
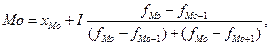 (15)
(15)
где 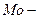 мода, наиболее часто повторяющееся значение признака;
мода, наиболее часто повторяющееся значение признака; 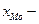 нижняя граница значения интервала, содержащего моду;
нижняя граница значения интервала, содержащего моду; 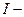 величина интервала;
величина интервала; 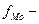 частота модального интервала;
частота модального интервала; 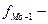 частота интервала, предшествующего модальному;
частота интервала, предшествующего модальному; 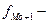 частота интервала, следующего за модельным.
частота интервала, следующего за модельным.
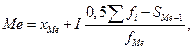 (16)
(16)
где 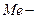 медиана, серединное значение признака;
медиана, серединное значение признака; 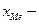 нижняя граница значения интервала, содержащего медиану;
нижняя граница значения интервала, содержащего медиану; 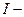 величина интервала;
величина интервала; 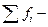 сумма частот;
сумма частот; 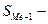 сумма накопленных частот, предшествующих медианному интервалу;
сумма накопленных частот, предшествующих медианному интервалу; 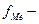 частота медианного интервала.
частота медианного интервала.
Моду и медиану можно определить графически.
Мода определяется по гистограмме распределения (Рис.4). Для этого выбирается самый высокий прямоугольник, который является модальным. Его вершины соединяются с вершинами предшествующего и последующего прямоугольников. Абсцисса точки пересечения этих прямых и будет модой распределения.
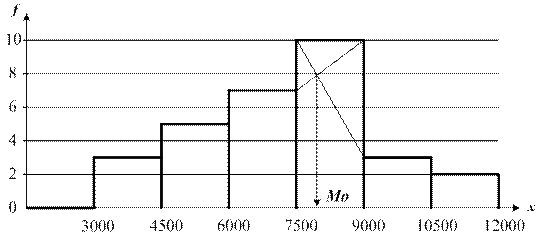
Рис.4 Графическое определение моды Мо
Медиана определяется по кумуляте. Для этого из точки на шкале частот, соответствующей 50%, проводится прямая, параллельная оси абсцисс до пересечения с кумулятой. Затем из точки пересечения опускается перпендикуляр на ось абсцисс, это значение и будет медианой.
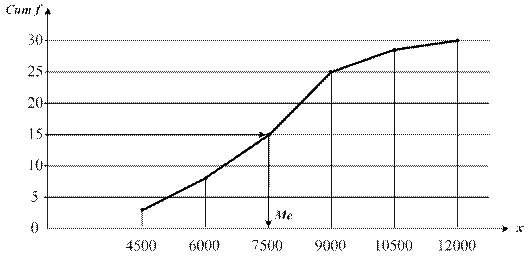
Рис.5 Графическое определение медианы Ме
Из графических построений следует, что мода составляет 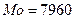 , величина медианы равна:
, величина медианы равна:  7500;
7500;
Аналитические значения моды и медианы: