Приближенный расчет потерь вызовов на участке ЦСИО

3.1.1 Выбор варианта заданий (см. таблицу 7) осуществляется по двум последним цифрам зачетной книжки студента при их сложении.

Т а б л и ц а 7 – Исходные данные

Данные	Варианты
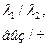
	400/	300/	250/	500/	350/	290/	180/	190/	200/
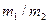
	4/7	3/5	7/9	6/9	2/6	8/10	5/8	3/9	6/10
	120/	210/	150/	180/	210/	120/	150/	120/	180/
Данные	Варианты
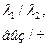
	170/	196/	290/	270/	320/	350/	360/	410/	420/
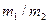
	5/9	6/11	3/7	8/14	4/16	9/15	7/9	5/12	8/13
	150/	180/	210/	120/	180/	210/	240/	210/	120/

3.1.2 Общие данные: пучок из = 30каналов поступают вызовы двух категорий, n=2.

3.1.3 Задание к работе:

- классифицировать мультимедийный трафик, проанализировать характеристики мультисервисной нагрузки, дать понятие скученности нагрузки и описать подход к параметризации мультимедийного трафика;

- определить общую интенсивность нагрузки на каналы от источников всех категорий;

- расчет дисперсии нагрузки на каналы от источников всех категорий;

- расчет коэффициента скученности нагрузки;

- расчет потерь.

3.1.4 Методические указания к выполнению работы. Для выполнения задания необходимо знать, что на полнодоступный пучок из V каналов поступает простейший поток вызовов с интенсивностью λ, причем каждый вызов требует для своего обслуживания одновременно m каналов, m < 1. Каналы занимаются на случайное время обслуживания, средняя продолжительность которого равна h, и при завершении процедуры обслуживания все каналы из группы одновременно освобождаются. Если в момент поступления вызова в пучке отсутствует необходимое число свободных каналов, то вызов теряется.

При определении вероятности потери вызова 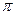для анализируемой системы, которую назовем системой S, непосредственное применение первой формулы Эрланга нельзя считать обоснованным в силу неординарного потока занятий каналов. Вместо этого исследуем модифицированную систему , состоящую из 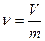комплектов, каждый из которых объединяет m каналов. Теперь отдельному поступившему вызову потребуется для обслуживания один такой комплект и, следовательно, поток занятия комплектов будет ординарным. Нагрузка в системе определяется числом занятых комплектов (а не каналов), т.е. совпадает с нагрузкой по вызовам и является пуассоновской с интенсивностью . Для расчета вероятности потерь вызова в системе можно воспользоваться первой формулой Эрланга:

(9)

С точки зрения статистических характеристик процесса обслуживания вызовов, системы S и полностью эквивалентны и очевидно, что 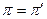. Отсюда с учетом соотношений:

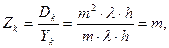(10)

и

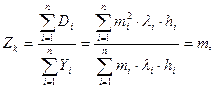(11)

следует:

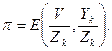(12)

В общем случае, когда мультисервисная нагрузка создается несколькими категориями источников с разной кратностью вызовов m_i, суперпозицию поступающих потоков заменяется одним потоком, который имеет такие же значения математического ожидания Y_k и дисперсии D_k нагрузки на каналы. В действительности непуассоновские потоки обладают достаточно сложными статистическим свойствами, и для полного описания таких потоков требуется использование большего числа характеристик, на практике обычно предполагают, что вероятность потери вызова слабо зависит от моментов нагрузки более высокого порядка и их можно не учитывать согласно утверждению – если известна вероятность потери вызова 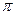в некотором пучке из V каналов при мультисервисной нагрузке с интенсивностью Y_k и коэффициентом скученности z_k, то в любом пучке с такими же параметрами V, Y_k, z_kи потери вызовов будут приближенно равны .

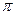Следовательно, вычислив коэффициент скученности объединенного потока вызовов по формуле (11), можно затем с помощью соотношения (12) определить вероятность потери произвольного вызова, что дает приближенную оценку средних (или общих) потерь. Между тем, для различных категорий источников нагрузки, как видно из неравенства , вызовы теряются при разных состояниях системы, и как следствие, вероятностные характеристики качества обслуживания вызовов будут отличаться. Для расчета индивидуальных потерь, т.е. вероятности потери вызова i -й категории, при i = 1, n, можно воспользоваться приближенным соотношением:

(13)

Таким образом, при обслуживании мультисервисной нагрузки, которая имеет непуассоновский характер, расчет потерь вызовов в исходной системе заменяется аналогичной задачей для эквивалентной системы, где такая задача может быть решена с использованием классических результатов теории Эрланга. Выражение (13) называют формулой Хейворда, которое является одним из наиболее простых вариантов метода эквивалентных замен. Применение формулы Хейворда предполагает наличие процедуры вычислений по первой формуле Эрланга при нецелых значениях числа линий x. Как одним из возможных вариантов, можно воспользоваться интерполяционной формулой:

(14)

где .

3.1.5 Численный пример.

Пусть на пучок из V =30 каналов поступают вызовы двух категорий, n =2 с требуемыми для обслуживания каналами 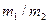(1, 4), с интенсивностью (300/100) и средней продолжительностью обслуживания 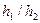(120/90). Требуется определить общие (средние) и индивидуальные потери вызовов.

Решение задачи проводится в следующей последовательности.

Определение общей интенсивности нагрузки на каналы от источников всех категорий:

(Эрл).

Вычисление дисперсии нагрузки на каналы от источников всех категорий:

(Эрл²).

Определение коэффициента скученности нагрузки:

(Эрл).

По формуле Хейворда с использованием таблиц Пальма определение средней вероятности потерь для общего потока поступающих вызовов:

.

Получение индивидуальных вероятностей потерь для вызовов 1-й и 2-й категорий:

, .
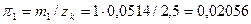