Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. На первый взгляд, следует применить формулу средней арифметической простой, но в течение рабочего дня ими было изготовлено разное число деталей.
|
|
На первый взгляд, следует применить формулу средней арифметической простой, но в течение рабочего дня ими было изготовлено разное число деталей.
Средние затраты времени на 1 деталь должны определяться по формуле

Затраты времени представляют собой произведение количества изготовленных деталей (f) и времени на изготовление одной детали (x). Поскольку затраты рабочего времени (xf) у обоих рабочих равны (рабочий день), то применим формулу средней гармонической простой.
Итак, 
 мин.
мин.
Пример 6. По имеющимся данным о ценах товара в различных фирмах города определить моду и медиану.
а) 4, 4 4, 3 4, 4 4, 5 4, 3 4, 3 4, 6 4, 2 4, 6
б) 4, 4 4, 3 4, 4 4, 5 4, 3 4, 3 4, 6 4, 2 4, 6 4, 1
Решение. В обоих случаях данные не сгруппированы.
а) в данной совокупности чаще всего повторяется значение 4, 3, поэтому Мо =4, 3
Для определения медианы надо провести ранжирование:
4, 2 4, 3 4, 3 4, 3 4, 4 4, 4 4, 5 4, 6 4, 6
В данном ряду нечетное число членов, варианта, расположенная посередине, является медианой. Ме =4, 4
б) в данной совокупности чаще всего повторяется значение 4, 3, поэтому Мо =4, 3
Для определения медианы проведем ранжирование:
4, 1 4, 2 4, 3 4, 3 4, 3 4, 4 4, 4 4, 5 4, 6 4, 6
В данном ряду четное число членов (10), поэтому медиана рассчитывается как средняя арифметическая из двух вариант, расположенных в центре ряда, т.е. Ме= (4, 3+4, 4)/2=4, 35
Пример 7. По имеющимся данным определить моду и медиану
| Количество филиалов в городе организации, х | Число банков f | Накопленные частоты S |
| 1 | ||
| 6 | ||
| 14 | ||
| Итого |
Решение. Данные представлены в виде дискретного ряда распределения.
Наибольшая частота f =8 соответствует варианте х =4, поэтому Мо = 4.
Для нахождения медианы следует рассчитать накопленные частоты. S= 14, впервые превысившая 10 (половину общей суммы частот), соответствует варианте х =4. Значит, Ме =4.
Пример 8. По имеющимся данным определить моду и медиану
| № группы | Размер прибыли, х | Число банков (частота) f | Накопленные частоты S | ||
| 3, 7 | - | 4, 6 | 3 | ||
| 4, 6 | - | 5, 5 | 6 | ||
| 5, 5 | - | 6, 4 | 13 | ||
| 6, 4 | - | 7, 3 | |||
| 7, 3 | - | 8, 2 | |||
| Итого |
Решение. Данные представлены в виде интервального ряда распределения ряда распределения.
Для расчета моды требуется сначала определить модальный интервал: наибольшая частота f =7 соответствует интервалу 5, 5 - 6, 4. Значит, это модальный интервал. Конкретное значение моды определяется по формуле:
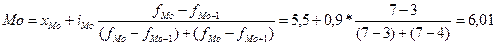
Для расчета медианы определим медианный интервал. Для этого рассчитаем накопленные частоты, пока они не превысят половину суммы частот (т.е. 10). S= 13 соответствует интервалу 5, 5-6, 4, значит, это медианный интервал. Конкретное значение медианы найдем по формуле: