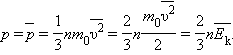Основное уравнение МКТ газов. Температура

Простейшей моделью молекулярно-кинетической теории является модель идеального газа. В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур. Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, газ, температура).

В результате каждого столкновения между молекулами и молекул со стенкой скорости молекул могут изменяться по модулю и по направлению; на интервалах между последовательными столкновениями молекулы движутся равномерно и прямолинейно. В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т. е. подчиняются законам механики Ньютона.

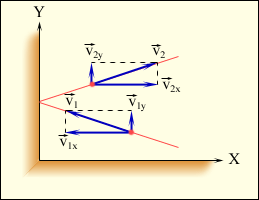
Используя модель идеального газа, вычислим давление газа на стенку сосуда. В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υ _x скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υ _y скорости, параллельная стенке, остается неизменной (рис. 3.2.1).

Рисунок 3.2.1. Упругое столкновение молекулы со стенкой.

Поэтому изменение импульса молекулы будет равно 2 m ₀υ _x, где m ₀ – масса молекулы.

Выделим на стенке некоторую площадку S (рис. 3.2.2). За время Δ t с этой площадкой столкнуться все молекулы, имеющие проекцию скорости υ _x, направленную в сторону стенки, и находящиеся в цилиндре с основанием площади S и высотой υ _xΔ t.

Рисунок 3.2.2. Определение числа столкновений молекул с площадкой S.

Пусть в единице объема сосуда содержатся n молекул; тогда число молекул в объеме цилиндра равно nS υ _xΔ t. Но из этого числа лишь половина движется в сторону стенки, а другая половина движется в противоположном направлении и со стенкой не сталкивается. Следовательно, число ударов молекул о площадку S за время Δ t равно Поскольку каждая молекула при столкновении со стенкой изменяет свой импульс на величину 2 m ₀υ _x, то полное изменение импульса всех молекул, столкнувшихся за время Δ t с площадкой S, равно 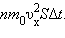По законам механики это изменение импульса всех столкнувшихся со стенкой молекул происходит под действием импульса силы F Δ t, где F – некоторая средняя сила, действующая на молекулы со стороны стенки на площадке S. Но по 3-му закону Ньютона такая же по модулю сила действует со стороны молекул на площадку S. Поэтому можно записать:

Разделив обе части на S Δ t, получим:

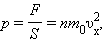
где p – давление газа на стенку сосуда.

При выводе этого соотношения предполагалось, что все n молекул, содержащихся в единице объема газа, имеют одинаковые проекции скоростей на ось X. На самом деле это не так.

В результате многочисленных соударений молекул газа между собой и со стенками в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а модули скоростей и их проекции на координатные оси подчиняются определенным закономерностям.

среднеквадратичная скорость 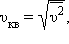где – среднее значение квадрата скорости.

Чтобы уточнить формулу для давления газа на стенку сосуда, предположим, что все молекулы, содержащиеся в единице объема, разбиты на группы, содержащие n ₁, n ₂, n ₃ и т. д. молекул с проекциями скоростей υ _x1, υ _x2, υ _x3 и т. д. соответственно. При этом 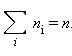Каждая группа молекул вносит свой вклад 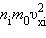в давление газа. В результате соударений со стенкой молекул с различными значениями проекций υ _xi скоростей возникает суммарное давление

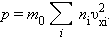
Входящая в это выражение сумма – это сумма квадратов проекций υ _x всех n молекул в единичном объеме газа. Если эту сумму разделить на n, то мы получим среднее значение 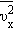квадрата проекции 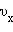скорости молекул:

Теперь формулу для давления газа можно записать в виде

Так как все направления для векторов скоростей молекул равновероятны, среднее значение квадратов их проекций на координатные оси равны между собой:

Последнее равенство вытекает из формулы:

Формула для среднего давления газа на стенку сосуда запишется в виде

Это уравнение устанавливает связь между давлением p идеального газа, массой молекулы m ₀, концентрацией молекул n, средним значением квадрата скорости и средней кинетической энергией 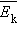поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов.

Таким образом, давление газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.

В основное уравнение молекулярно-кинетической теории газов входит произведение концентрации молекул n на среднюю кинетическую энергию 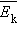поступательного движения. Если предположить, что газ находится в сосуде неизменного объема V, то 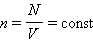(N – число молекул в сосуде). В этом случае изменение давления Δ p пропорционально изменению 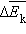средней кинетической энергии.

Возникают вопросы: каким образом можно на опыте изменять среднюю кинетическую энергию движения молекул в сосуде неизменного объема? Какую физическую величину нужно изменить, чтобы изменилась средняя кинетическая энергия 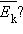Такой величиной в физике является температура.

Понятие температуры тесно связано с понятием теплового равновесия. Тела, находящиеся в контакте друг с другом, могут обмениваться энергией. Энергия, передаваемая одним телом другому при тепловом контакте, называется количеством теплоты.

Тепловое равновесие – это такое состояние системы тел, находящихся в тепловом контакте, при котором не происходит теплопередачи от одного тела к другому, и все макроскопические параметры тел остаются неизменными. Температура – это физический параметр, одинаковый для всех тел, находящихся в тепловом равновесии. Возможность введения понятия температуры следует из опыта и носит название нулевого закона термодинамики.

Для измерения температуры используются физические приборы – термометры, в которых о величине температуры судят по изменению какого-либо физического параметра. Для создания термометра необходимо выбрать термометрическое вещество (например, ртуть, спирт) и термометрическую величину, характеризующую свойство вещества (например, длина ртутного или спиртового столбика). В различных конструкциях термометров используются разнообразные физические свойства вещества (например, изменение линейных размеров твердых тел или изменение электрического сопротивления проводников при нагревании).

Термометры должны быть откалиброваны. Для этого их приводят в тепловой контакт с телами, температуры которых считаются заданными. Чаще всего используют простые природные системы, в которых температура остается неизменной, несмотря на теплообмен с окружающей средой – это смесь льда и воды и смесь воды и пара при кипении при нормальном атмосферном давлении. По температурной шкале Цельсия точке плавления льда приписывается температура 0 °С, а точке кипения воды – 100 °С. Изменение длины столба жидкости в капиллярах термометра на одну сотую длины между отметками 0 °С и 100 °С принимается равным 1 °С. В ряде стран (США) широко используется шкала Фаренгейта (T _F), в которой температура замерзающей воды принимается равной 32 °F, а температура кипения воды равной 212 °F. Следовательно,

Особое место в физике занимают газовые термометры (рис. 3.2.4), в которых термометрическим веществом является разреженный газ (гелий, воздух) в сосуде неизменного объема (V = const), а термометрической величиной – давление газа p. Опыт показывает, что давление газа (при V = const) растет с ростом температуры, измеренной по шкале Цельсия.

Рисунок 3.2.4. Газовый термометр с постоянным объемом.

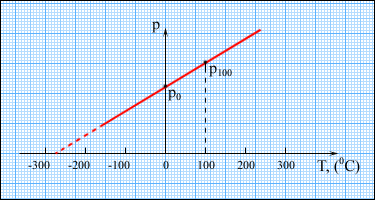
Чтобы проградуировать газовый термометр постоянного объема, можно измерить давление при двух значениях температуры (например, 0 °C и 100 °C), нанести точки p ₀ и p ₁₀₀ на график, а затем провести между ними прямую линию (рис. 3.2.5). Используя полученный таким образом калибровочный график, можно определять температуры, соответствующие другим значениям давления. Экстраполируя график в область низких давлений, можно определить некоторую «гипотетическую» температуру, при которой давление газа стало бы равным нулю. Опыт показывает, что эта температура равна –273, 15 °С и не зависит от свойств газа. Невозможно на опыте получить путем охлаждения газ в состоянии с нулевым давлением, так как при очень низких температурах все газы переходят в жидкие или твердые состояния.

Рисунок 3.2.5. Зависимость давления газа от температуры при V = const.

Английский физик У. Кельвин (Томсон) в 1848 г. предложил использовать точку нулевого давления газа для построения новой температурной шкалы (шкала Кельвина). В этой шкале единица измерения температуры такая же, как и в шкале Цельсия, но нулевая точка сдвинута:

В системе СИ принято единицу измерения температуры по шкале Кельвина называть кельвином и обозначать буквой K. Например, комнатная температура T _С = 20 °С по шкале Кельвина равна T _К = 293, 15 К.

Температурная шкала Кельвина называется абсолютной шкалой температур. Она оказывается наиболее удобной при построении физических теорий.

Нет необходимости привязывать шкалу Кельвина к двум фиксированным точкам – точке плавления льда и точке кипения воды при нормальном атмосферном давлении, как это принято в шкале Цельсия.

Кроме точки нулевого давления газа, которая называется абсолютным нулем температуры, достаточно принять еще одну фиксированную опорную точку. В шкале Кельвина в качестве такой точки используется температура тройной точки воды (0, 01° С), в которой в тепловом равновесии находятся все три фазы – лед, вода и пар. По шкале Кельвина температура тройной точки принимается равной 273, 16 К.

Газовые термометры громоздки и неудобны для практического применения: они используются в качестве прецизионного стандарта для калибровки других термометров.

Таким образом, давление разреженного газа в сосуде постоянного объема V изменяется прямо пропорционально его абсолютной температуре: p ~ T. С другой стороны, опыт показывает, что при неизменных объеме V и температуре T давление газа изменяется прямо пропорционально отношению количества вещества ν в данном сосуде к объему V сосуда

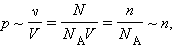
где N – число молекул в сосуде, N _A – постоянная Авогадро, n = N / V – концентрация молекул (т. е. число молекул в единице объема сосуда). Объединяя эти соотношения пропорциональности, можно записать:

где k – некоторая универсальная для всех газов постоянная величина. Ее называют постоянной Больцмана, в честь австрийского физика Л. Больцмана (1844–1906 гг.), одного из создателей молекулярно-кинетической теории. Постоянная Больцмана – одна из фундаментальных физических констант. Ее численное значение в СИ равно:

Сравнивая соотношения p = nkT с основным уравнением молекулярно-кинетической теории газов, можно получить: