
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Короткі теоретичні відомості
|
|
Цифрова обрабка сигналів в ПК виконується за обмеженної в часі реалізації аналогового сигналу s(t), квантованого по рівню и дискретизованому в часі за допомогою АЦП.
Процес формування реализації сигналу у часі може бути представлений як результат множення трьох сигналів:
- власне не обмеженного у часі аналогового сигналу s(t), характеристики якого досліджуються;
- функції часового вікна w(t), що обмежує сигнал у часі тривалістю реализації Тр;
- функції дискретизації обмеженного в часі аналогового сигналу Ш(t) (функция Шенона) із частотою дискретизації fs або часом дискретизації ∆ ts = 1/fs.
Як результат аналізується не початковий аналоговий сигнал s(t), а його дискретна реализація s(n) тривалістю Тр = Np*∆ ts, де Np – кількість виборок у реализації або об’єм реализації.
Сигнал s(t), як добуток функцій, відображається в спектральній області згорткою їх фурье-образів,
s(n) = s(t)∙ w(t)∙ Ш(t) ↔ S(ω)*W(ω)*Ш(ω) = SN(ω) (1)
що значно позначається на спектральних характеристиках сигналу й на результатах його подальшого перетворення і обробки. Зокрема, при спектральному анализі окремі гармоничні складові спектру сигналу виявляються «розмитими» й представляються декількома спектральними складовими замість однієї.
Найпростішою функцією часового вікна є прямкутна функція із одиничним амплитудним значенням й тривалістю Тр (прямоугольный импульс), яку називають природним часовим вікном або природньою ваговою функцією (П-вікном або прямокутним вікном). На рис.1 представлені графіки прямокутного вікна тривалістю Тр=1с (позначено потовшенною лінією), реалізації гармонічного сигналу частотою 5 Гц, що отриманий за допомогою цього вікна (рис.1а) та комплексний амплітудний спектр прямокутної віконної функції W(ω) (рис.1b).
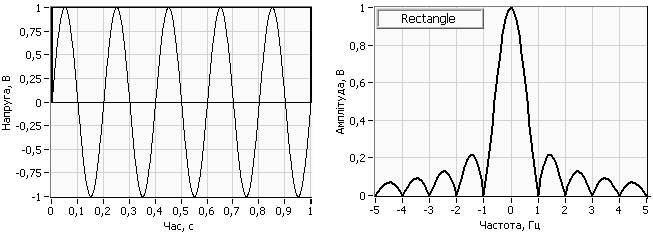
а. b.
Рис.1. Функція прямокутного вікна Rectangle та її комплексний спектр амплітуд
Множення гармонічного сигналу s(t) (гармонічних складових) на функцію вікна w(t) спотворює спектр гармонічного сигналу: відбувається перенос спектра функції вікна W(ω) (рис.1b) на частоту гармонічного сигналу S(ω) (рис.2a). Це призводить до “розмивання” спектру гармонічного сигналу по осі частот (рис.2b).
Спектральній аналіз реалізації сигналів виконується обчисленням обмеженного числа частотних складових Nf =Np/2 у точках, частоти яких кратні базовій частоті f0=1/Тр, тобто на частотах fі = і∙ f0. Таким чином спетр обмеженної в часі реалізації сигналу обчислюється як дискретний за частотою із кроком f0.
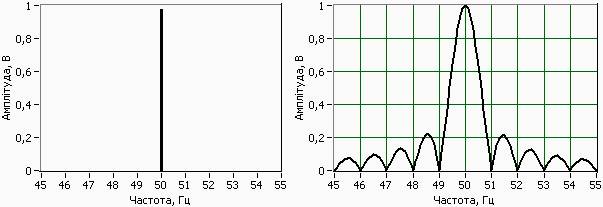 а. b.
а. b.
Рис.2. Спектр гармонічного сигналу до та після обробки віконною функцією
Якщо представити спектр реалізації гармонічного сигналу (рис.2b) окремими частотними відліками із кроком f0, то вигляд спектру буде залежати від розташування частоти гармоніки (центральної частоти спектру сигналу) відносно дискретизуючих частотних відліків. Наприклад, при тривалості реалізації Тр=1с, крок дискретизації за частотою у наведенному прикладі f0=1 Гц, а частоти у яких будуть обчислюватись спектральні складові fi=i∙ 1Гц й будуть у данному випадку цілими числами, тобто 45, 46, 47…55 Гц. Якщо частота гармонічного сигналу (або гармонічна складова) співпадає з частотою частотного відліку, як на рис.2b (fs=50 Гц), то спектральні складові в точках 45, 46…55 Гц будіть дорівнювати практично 0, крім точки 50 Гц, де амплітуда складової буде становити 1 В. В цьому випадку результуючий спектр буде таким, як на рис.2а, тобто представляти ідеальний гармонічний сигнал. При цьому кількість періодів гармонічного сигналу, що укладається у час реалізації Тр становить ціле число. Дійсно Tp/Ts=fs/f0=50. В інших випадках не кратного співвідношення періода гармоніки і тривалості реалізації обчислений спектр не буде відповідати спектру сигналу s(t). Найгірша ситуація буде у випадку, коли частота сигналу буде знаходитись посередені частотних відліків, що обчислюються, наприклад на частоті 49, 5 Гц. В цьому випадку сусідні частотні відліки, що обчислюються попадають на піки пелюстків спектру обмеженної в часі реалізації гармонічного сигналу (рис.3).

а. б.
Рис.3. Спектр гармонічного сигналу з некратним періодом
На рис.3 видно суттєве розмивання спектру гармоніки по сусідніх частотних відліках, що призводить до зниження розподільної здатності спектрального аналізу частотних компонент сигналу, що знаходяться поруч, значно відрізняються рівнем й маскуються більш “сильними” компонентами. Крім того, при необхідності вимірювання рівня гармонік по спектру сигналу виникають амплітудні похибки більше 30%.
Для зменшення розмивання спектрів гармонік та похибок вимірювання використовуються часові вікна іншої форми ніж прямокутне. На теперешній час відомо декілька десятків вагових часових функцій, які відрізняються формою, що поліпшує характеристики спектру гармонік сигналу в окремих його частинах. Вибір типу вікна залежить від типу сигналу, що досліджується, а також від того, які його характеристики досліджуються. У таблиці 1 наведені рівняння деяких віконних функцій у дискретній формі та сфери їх застосування. На рис. 4 дан приклад віконних функції Hanning, Flat Top й наведено їх спектри.
Таблиця 1. Основні часові функції
| Вікно | Рівняння | Використання |
| Rectangle | W[n] = 1, 0 | Дослідження перехідних характеристик менших за тривалість вікна, виділення окремих близьких за частотою складових з близькими амплітудами |
| Henning | W[n] = 0.5-0.5cos(2π n/Np) | Системний аналіз, аналіз випадкових процесів, дослідження перехідних характеристик більших за тривалість вікна |
| Hemming | W[n] = 0.54 – 0.46cos(2π n/Np) | Аналогічно Henning, виділення окремих близьких за частотою складових з різними по рівню амплітудами |
| Blackman | W[n] = 0.42 – 0.5cos(2π n/Np) +0.08cos(4π n/Np) | Аналогічно Henning та Hemming із зменшенням «пульсацій» |
| Flat Top | W[n]=0.21557895 -0.41663158cos(2π n/Np)+0.277263158cos(4π n/Np) -0.083578947cos(6π n/Np) +0.006947368cos(8π n/Np) | Точне вимірювання амплітуди окремої гармоніки при відсутності найближчих частотних компонент |
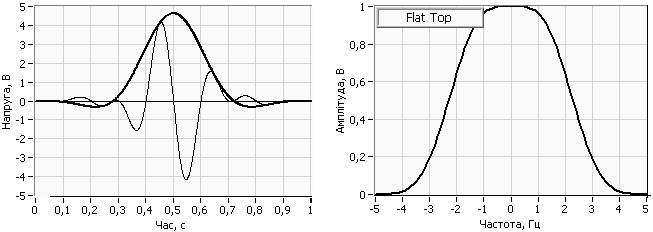
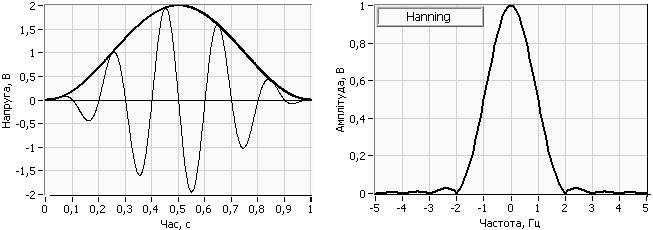
Рис.4. Віконні функції Hanning та Flat Top
Спектри віконних функцій наведенних на рис.1 та 4 відрізняються формою головного пелюстка, (його шириною, «площиною» його верхівки), рівнем бокових пелюстків і т. ін. Для порівняння віконних функцій використовують три основні крітерії порівняння:
- відношення а амплітуди найбільшого із бічних пелюстків до амплітуди головного пелюстка;
- відносна амплітудна похибка спектрального аналізу b – відношення максимального рівня головного пелюстка на центральній частоті до рівня на частоті, що відрізняється від центральної на ±0, 5∆ f0;
- ширина головного пелюстка ∆ f, що обчислюється частотною полосою на рівні -3 дБ, або 0, 707 від максимального рівня головного пелюстка на центральній частоті.
Використовуючи наведенні крітерії можна оптімально вибрати віконні функції, що до задач спектрального аналізу різних сигналів.