Виды средних величин

Формулы для расчета степенных средних можно представить в виде следующей таблицы:

Наименование	Формула	Условия применения
средняя гармоническая простая		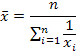(k =-1) вычисляется в тех случаях, когда приходится суммировать не сами варианты, а обратные им величины
средняя гармоническая взвешенная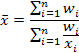
средняя геометрическая простая		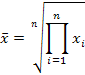(k =0) используется в тех случаях, если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин
средняя геометрическая взвешенная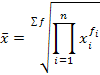
средняя арифметическая простая		(k =1) исчисляется в тех случаях, когда объем варьирующего признака для всей совокупности образуется как сумма значений признака отдельных ее единиц
средняя арифметическая взвешенная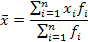
средняя квадратическся простая		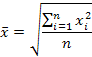(k =2) применяется в тех случаях, если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин
средняя квадратическся взвешенная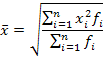

Формулы для расчета структурных средних можно представить в виде следующей таблицы:

Наименование	Формула
Мода в дискретном ряду	варианта с наибольшей частотой
Мода в интервальном ряду
Медиана в дискретном ряду	признак приходящееся на середину упорядоченной (ранжированной) совокупности
Медиана в интервальном ряду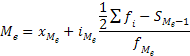
Нижний квартиль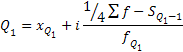
Верхний квартиль

где: - нижняя граница модального интервала;

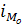- величина модального интервала;

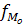- частота модального интервала;

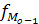- частота следующая за модальным интервалом;

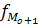- частота предшествующая модальному интервалу;

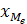- начальное значение медианного интервала;

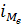- величина модального интервала;

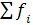- сумма частот ряда;

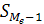- накопленная частота интервала предшествующая медианному интервалу;

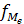- частота медианного интервала;

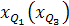- нижняя граница интервала, содержащего нижний (верхний) квартиль;

i - величина интервала;

- накопленная частота интервала, предшествующего интервалу, содержащему нижний (верхний) квартиль;

- частота интервала, содержащего нижний (верхний) квартиль.