I. Задача безусловной оптимизации

Лабораторная работа №1

1. ЗАДАЧА БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Задача оптимизации формулируется следующим образом:

заданы множество Х (допустимое множество задачи) и функция f(x) (целевая функция), определенная на Х; требуется найти точки минимума или максимума функции f на Х. Задача оптимизации, в которой целевая функция подлежит минимизации, имеет вид

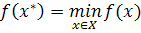
В курсе рассматриваются задачи, допустимое множество которых лежит в евклидовом пространстве Rⁿ.

Точка x^∗ ∈ X называется точкой глобального минимума f(x) на множестве X, или глобальным решением задачи оптимизации, если

f(x*) ≤ f(x) при всех х∈ Х

Точка x^∗ ∈ X называется точкой локального минимума f(x) на множестве X, или локальным решением задачи оптимизации, если

f(x*) ≤ f(x) при всех х∈ Х∩ Vε (x*)

где Vε (x*= { х∈ Хⁿ: ║ x- x*║ ≤ ε } − шар радиуса ε > 0 с центром в точке x* (ε - окрестность точки x*).

Ясно, что глобальное решение является и локальным; обратное неверно.

ФУНКЦИЯ ОДНОЙ ПЕРЕМЕННОЙ

Для функции одной переменной условия оптимальности формулируются следующим образом.

Необходимое условие локальной оптимальности. Пусть f(x) дифференцируема в точке x^∗ ∈ R¹ Если x^∗ − точка локального оптимума (экстремума), то.

f′ (x*)=0

Точки, удовлетворяющие данному условию, называются стационарными. Стационарные точки могут быть и точками локального минимума, и точками локального максимума, и точками перегиба. Для определения характера стационарных точек используется достаточное условие локальной оптимальности.

Достаточное условие локальной оптимальности. Пусть f(x) k раз, k> 1, дифференцируема в точке x^∗ ∈ R¹, причем

f′ (x*)=f ′ ′ (x*)=…= f^{′ (k-1)}(x*)=0, f^{′ (k)}(x*) ≠ 0

Тогда, если k − четное число, то x* − точка локального минимума (максимума) при f^{′ (k)}(x*) > 0) (при f^{′ (k)}(x*) < 0). Если k − нечетное число, то x^∗ − точка перегиба.

Используя необходимое и достаточное условия оптимальности, находятся точки локальных экстремумов. Для определения точек глобальных экстремумов вычисляются предельные (при x → ∞ и x → − ∞) значения f(x). Если

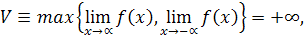
то f(x) не имеет конечного глобального максимума. Если

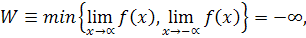
то f(x) не имеет конечного глобального минимума.

Если f(x) имеет конечный глобальный максимум и (или) конечный глобальный минимум, то для их определения вычисляются также значения f(x) на множестве точек локальных экстремумов. Наименьшее из полученных значений, т.е. значений f(x) в точках локальных экстремумов и предельных значений f(x), определяет точку глобального минимума, наибольшее из полученных значений − точку глобального максимума f(x).

Алгоритм определения точек экстремумов функции одной переменной

1. Находится f ′ (x).

2. Вычисляются корни уравнения f ′ (x) =0 – стационарные точки

x_{(i )}, i∈ I={1, 2, …, N}, где N − число стационарных точек. Полагается k =2..

3. Находится f^(k)(x)

4. Вычисляются значения f^(k)(x_(i)) для всех. i∈ I

Если f^(k)(x_(i)) ≠ 0, то определяется тип стационарной точки x_{(i )}, и ее номер исключается из множества I.

5. Проверяется условие определения типа всех стационарных точек

I=∅.

Если оно выполняется, то осуществляется переход к п.6. Если условие не выполняется, то полагается k=k+1 и осуществляется переход к п.3.

6. Вычисляются предельные (при x → ∞ и x → − ∞) значения f(x). Если f(x) не имеет конечных глобальных экстремумов, то вычисления прекращаются. В противном случае осуществляется переход к п.7.

7. Вычисляются значения f(x) на множестве точек локальных экстремумов. По наименьшему из полученных значений f определяется точка глобального минимума, по наибольшему из полученных значений f − точка глобального максимума.

1. Определить точки локальных и глобальных экстремумов функции

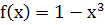
2. Определить точки локальных и глобальных экстремумов функции

3.Определить точки локальных и глобальных экстремумов функции

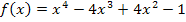
4. Определить точки локальных экстремумов функции

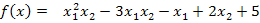
5. Определить точки локальных экстремумов функции

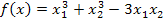
6. Проверить, что точки x₍₁₎ =(0, 3, 1), x₍₂₎=(0, 1, -1) и x₍₃₎=(1, 2, 0) являются стационарными точками функции

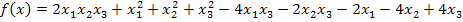
Определить, какие из приведенных точек являются точками экстремумов данной функции.

7. Определить, являются ли точки x₍₁₎ =(0, 1), x₍₂₎=(2, 1) точками экстремумов функции
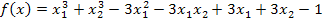