
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Измерение активности источников бета-частиц
|
|
Общие замечания. Способы регистрации α - и β -частиц во многом аналогичны. Однако существенные различия в поведении этих частиц при их прохождении через вещество накладывают некоторые особенности на конструкцию детекторов.

Рис. 10.4. Устройство для измерений с торцевым счетчиком:
1 — источник β - частиц; 2 — свинцовая защита; 3 — стойка из плексигласа; 4 — торцевой β -счетчик.

Рис. 10.5. Схема пропорционального 4π — β -счетчика:
1 — нити счетчика; 2 — источник; 3 — корпус
С одной стороны, значительно большие пробеги β -частиц позволяют изготавливать детекторы с гораздо более толстыми стенками. С другой стороны, сильное рассеяние β -частиц и меньшая ионизирующая способность затрудняют их регистрацию, тогда как регистрация α -частицы, попавшей в рабочее тело детектора, происходит практически со 100 %-ной вероятностью.
Измерения с малыми телесными углами. В качестве детекторов при измерениях этого типа используют обычно торцевые счетчики Гейгера — Мюллера (рис. 10.4). Из-за отмеченных выше особенностей взаимодействия β -частиц с веществом определить эффективность установки сложнее, чем при регистрации α -частиц. В общем виде:
ε = ε дGfиfpfo, (10.18)
где fо — коэффициент, учитывающий поглощение и рассеяние β -частиц в окне счетчика и в воздушной прослойке между счетчиком и источником. Остальные коэффициенты те же, что и для α -частиц но определяют их значения несколько иначе.
Геометрический фактор для точечного источника:
 (10.19)
(10.19)
(рис. 10.4). Для неточечного источника радиус которого г много меньше расстояния между источником и детектором d,
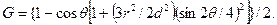 (10.20)
(10.20)
Чтобы получить правильные результаты с помощью этих формул, необходимо учесть возможные искажения электрического поля вблизи окна счетчика и необходимость прохождения электроном в газе счетчика некоторого минимального отрезка пути для появления электрического импульса. Оба эти фактора* учитываются при определении угла 6: берется не истинное окно счетчика, а сечение счетчика, отстоящее на 4-5 мм от окна.
Так же как и для α -частиц, в большинстве случаев ε д=1. Однако из-за меньшей плотности ионизации некоторые β -частицы, пробегающие в чувствительном объеме счетчика малые отрезки пути, имеют заметную вероятность не создать ни одной пары ионов. В счетчиках с пониженным давлением газовой смеси этот эффект особенно заметен. Поэтому в общем случае при прецизионных измерениях приходится на основании данных о плотности ионизации оценивать значение ε д, которое несколько меньше 1.
При определении коэффициента fи приходится учитывать не только поглощение, но и рассеяние β -частиц в источнике. Эти два фактора действуют по-разному: поглощение в источнике уменьшает число отсчетов счетчика, а рассеяние электронов увеличивает, так как рассеиваются в основном электроны, летящие вдоль слоя. В тонких слоях эффект рассеяния компенсирует или может даже превышать эффект поглощения, однако с увеличением толщины источника поглощение становится доминирующим. Величина fи зависит от толщины источника, энергия β -частиц и атомного номера вещества источника Z. Для средних значений Z и толщины источника порядка 1/20 пробега коэффициент fи очень близок к 1. В остальных случаях значение коэффициента fи лучше всего находить экспериментально, приготавливая источники разной толщины и экстраполируя к нулевой толщине измеряемые удельные скорости счета, т. е. скорости счета, отнесенные к толщине слоя (в мг/см2). Однако из-за немонотонного характера зависимости fH от толщины слоя надежность этой процедуры не очень высока и возникающие погрешности могут достигать 20% вносимой поправки, т.е. отличия fи от 1.
Коэффициент fр, равный отношению количеств регистрируемых импульсов с подложкой и без нее, может иметь значения от 1 до 2 в зависимости от толщины и атомного номера материала подложки. Проще всего его определить экспериментально, меняя материал подложки и ее толщину. Использование толстых подложек из тяжелых материалов может привести к увеличению скорости счета на 50–60%, тогда как применение материалов с малым Z при толщине подложки меньше Vs пробега электрона с максимальной энергией приводит к гораздо меньшим поправкам, поэтому более предпочтительно. Исходя из этих соображений, источник не следует класть на дно защитного «домика», а располагать его на расстоянии нескольких сантиметров от поверхности свинца.
Рассеяние электронов от дна и стенок защитного домика можно сделать пренебрежимо малым, если покрыть внутри домика все
детали слоем вещества с малым Z и расположить их подальше от траекторий электронов, летящих из источника в счетчик.
Коэффициент fo в (10.18) находят обычно также экспериментально: между источником и счетчиком помещают алюминиевые фольги различной толщины (алюминий, слюда и воздух имеют примерно одинаковые массовые коэффициенты поглощения β - частиц), снимают зависимость числа отсчетов счетчика от общей толщины материала (мг/см2), а затем экстраполируют полученные результаты к нулевой толщине. Значение f о очень сильно зависит от энергии β - частиц. Так, окошко из слюды толщиной 3 мг/см2 поглощает около 7 % частиц при максимальной энергии β - спектра 1 МэВ и 30 % при энергии 0, 5 МэВ. Если поправка на поглощение очень большая, то определение значений fo методом экстраполяции ненадежно. Рассеяние в воздухе при расстояниях между источником и окном счетчика порядка нескольких сантиметров и при малой энергии β - частиц может увеличивать число отсчетов до 5%.
Соответствующую поправку можно найти, откачивая воздух из домика или изменяя расстояние между счетчиком и источником.
Типичное значение е при регистрации β - частиц в геометрии с малым телесным углом с учетом всех перечисленных выше факторов порядка 0, 03. Из-за большого числа поправок, многие из которых находятся с недостаточно высокой точностью, суммарная погрешность получается довольно большой, достигая 5–10 %, и лишь в отдельных наиболее благоприятных случаях ее удается снизить до 2–3 %. Поэтому метод малого телесного угла чаще используют для относительных измерений.
4π – β -счетчики. Для измерений активности β - источников метод 4π -геометрии особенно эффективен, так как он позволяет исключить необходимость внесения большинства трудно определяемых поправок. 4я-геометрия реализуется расположением β - источника между двумя пропорциональными, сцинтилляционными или полупроводниковыми счетчиками (рис. 10.5). Источник и подложка, на которую он нанесен, должны быть достаточно тонкими, чтобы поправочные коэффициенты fи и fр на поглощение β -частиц в них были невелики (рассеяние β -частиц в материале источника и в подложке в 4π – β - счетчике несущественно). Кроме того, нет необходимости точно вычислять фактор G, который равен примерно 1, а также находить коэффициент fo. В результате формула для определения ε существенно упрощается:
ε = ε Д fиfp, (10.21)
а входящие в нее величины находятся гораздо проще и с большей точностью, чем в предыдущем случае. В целом е весьма близка к 1. Погрешности при определении активности связаны, в основном, со статистической неопределенностью в числе зарегистрированных импульсов, с исключением фона, с поправками на мертвое время, атакже с погрешностями при определении коэффициентов fи и fp. В целом погрешность можно снизить до 0, 3—0, 5 %.
Следует отметить, что при измерениях в 4π -геометрии применение сцинтилляционных счетчиков вместо пропорциональных часта более удобно по конструктивным соображениям, однако из-за высокого энергетического порога таких счетчиков значение ε д для β -частиц малых энергий может снижаться вплоть до 0.
Введение β -излучателя в рабочее тело детектора. Если радиоактивное вещество находится в каком-либо газе, например в воздухе,, то его активность проще всего определить, введя этот газ прямо в ионизационную камеру. Таким образом измеряют, в частности, содержание радиоактивного изотопа 14С в углекислом газе. Аналогичный прием используют в дозиметрии для непрерывного контроля содержания радиоактивных веществ в воздухе рабочих помещений. Особенно эффективен этот метод для регистрации β - излучения с малой -энергией. Типичным излучателем β - частиц малой энергии является тритий, у которого верхняя граница β - спектра лежит при энергии 18, 5 кэВ. Этой энергии соответствует пробег электронов в слюде, равный всего 0, 7 мг/см2, тогда как толщина окошка стандартных бета-счетчиков 2–3 мг/см2. Очевидно, что β - частицы состоль малой энергией можно регистрировать, только при условии введения β - излучателя в рабочий объем камеры или счетчика (обычно проточного). Зато при столь малой энергии нетрудно создать условия, при которых весь пробег электрона укладывается в газе счетчика, что позволяет измерить энергию β - частиц по амплитуде электрических импульсов.
При введении β - излучателя в газовую среду детектора можно считать, что в (10.6) все коэффициенты равны 1, кроме поправочных множителей на эффективный рабочий объем счетчика и на стеночный эффект. Если β - излучатель вводится в виде раствора в жидкий сцинтиллятор, то и эти множители обращаются в 1, зато появляются поправки на просчеты электронов малых энергий и на адсорбцию введенного вещества на стенках. Последнюю из них можно существенно снизить сильным разбавлением вводимого вещества растворителем. В целом погрешность подобных измерений порядка 1—2 %.
Метод β -γ - совпадений. Этот метод можно использовать, если β -распад сопровождается испусканием фотонов. Для определения активности формула (10.11) непосредственно применима лишь при простой схеме β - распада (рис. 10.6, а). В других случаях в нее приходится вводить поправки. Рассмотрим в качестве примера β - распад по двум ветвям β 1 и β 2 (рис. 10.6, 6) с относительными вероятностями w1 и w2 (w1+w2=1). При этом
aβ = (w1ε β 1+ w2ε β 2) A; (10.22)
aγ = w2ε γ A; (10.23)
aβ γ = w2ε β 2ε γ A; (10.24)
aβ aγ / aβ γ =(w1ε β 1/ ε β 2+w2)A. (10.25)
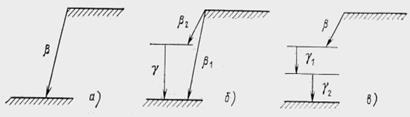
Рис. 10.6. Различные схемы β -распада:
а — распад по одной ветви; б — распад по двум ветвям; в — распады «I испусканием двух фотонов

Рис. 10.7. Зависимость эффективности счетчика ε Д от энергии γ - излучения для трех материалов катода; пунктир — расчетная кривая
При оценке абсолютных значений эффективностей ε β 1 и ε β 2 могут возникнуть, как было показано выше, существенные погрешности. Поэтому целесообразно применять для регистрации β -частиц 4л— β -счетчик. В этом случае ε β 1 = ε β 2 = 1 и (10.25) превращается в гораздо более простую формулу (10.11). Аналогичным образом можно рассчитать поправки и для других схем распада, а также поправки на конечные размеры источника, причем всегда применение 4π – β - счетчика для регистрации β - частиц позволяет получить наиболее простую расчетную формулу и наиболее достоверные результаты. Общая погрешность при измерении активности β - источников методом 4π β — γ -совпадений обычно составляет 0, 2—0, 5 %.