
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Непрерывные случайные величины. Если рассматривать случайную величину Х, значения которой заполняют интервал (a,b) и составить перечень всех возможных её значений невозможно
|
|
Если рассматривать случайную величину Х, значения которой заполняют интервал (a, b) и составить перечень всех возможных её значений невозможно, то она называется непрерывной. В результате этого появилась необходимость дать общий способ задания любых типов случайных величин. Для этого вводится функция распределения вероятностей случайной величины. Функция распределения F(х) для непрерывной случайной величины имеет вид
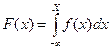
Функция f(х) называется плотностью вероятности:
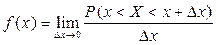
Непрерывная случайная величина задается либо функцией распределения F(х) (интегральным законом распределения), либо плотностью вероятности f(х) (дифференциальным законом распределения).
Cвойства функции распределения F(х):
1. Значения функции распределения F(х) принадлежат отрезку [0, 1]:
0 £ F(x) £ 1.
2. F(х) – неубывающая функция: F(x2) ³ F(x1), если x2 > x1.
Следствие_1. Вероятность того, что случайная величина примет значение, заключенное в интервале [ a, b ] равна приращению функции распределения на этом интервале P(a £ X < b)=F(b)-F(a).
3. Если возможные значения случайной величины принадлежат интервалу [ a, b ], то: F(x) =0 при x £ a; F(x) =1 при x ³ b. Геометрически это означает, что полная площадь, ограниченная кривой распределения и осью абсцисс равна единице.
Cвойства плотности вероятности f(х):
1. Плотность вероятности не может быть отрицательной функцией. f(x)³ 0.
2. Несобственный интеграл от плотности распределения в пределах
от – ¥ до + ¥ равен единице.
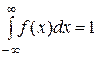
Основные характеристики непрерывной случайной величины:
I. Математическое ожидание непрерывной случайной величины Х определяется по формуле:
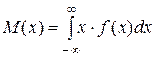
f(х) – плотность вероятности распределения случайной величины Х.
II. Дисперсия непрерывной случайной величины Х может быть вычислена по формулам:
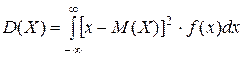
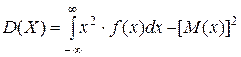
III. Среднее квадратическое отклонение определяется формулой 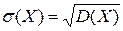 .
.
Если математическое ожидание случайной величины даёт «ее среднее значение» или точку на координатной прямой, «вокруг которой разбросаны» значения рассматриваемой случайной величины, то дисперсия характеризует «степень разброса» значений случайной величины около её среднего.