
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Структурные средние величины (мода и медиана)
|
|
Для определения структуры совокупности используют особые средние показатели, к которым относятся медиана и мода или так называемые структурные средние. Если средняя арифметическая рассчитывается на основе использования всех вариантов значений признака, то медиана и мода характеризуют величину того варианта, который занимает определенное среднее положение в ранжированном вариационном ряду
Мода — наиболее типичное, чаще всего встречаемое значение признака. Для дискретного ряда модой будет являться вариант с наибольшей частотой. Для определения моды интервального ряда сначала определяют модальный интервал (интервал, имеющий наибольшую частоту). Затем в пределах этого интервала находят то значение признака, которое может являться модой.
Чтобы найти конкретное значение моды интервального ряда, необходимо использовать формулу (3.2)
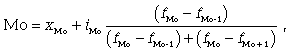 (3.2)
(3.2)
где ХМо - нижняя граница модального интервала; iМо - величина модального интервала; fМо - частота модального интервала; fМо-1 - частота интервала, предшествующего модальному; fМо+1 - частота интервала, следующего за модальным.
Мода имеет широкое распространение в маркетинговой деятельности при изучении покупательского спроса, особенно при определении пользующихся наибольшим спросом размеров одежды и обуви, при регулировании ценовой политики.
Медиана — значение варьирующего признака, приходящееся на середину ранжированной совокупности. Для ранжированного ряда с нечетным числом индивидуальных величин (например, 1, 2, 3, 6, 7, 9, 10) медианой будет величина, которая расположена в центре ряда, т.е. четвёртая величина - 6. Для ранжированного ряда с четным числом индивидуальных величин (например, 1, 5, 7, 10, 11, 14) медианой будет средняя арифметическая величина, которая рассчитывается из двух смежных величин. Для нашего случая медиана равна (7+10)/2= 8, 5.
Т. о., для нахождения медианы сначала необходимо определить ее порядковый номер (ее положение в ранжированном ряду) по формулам (3.3):
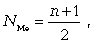 (если частот нет)
(если частот нет)
N Me = 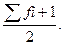 (если частоты есть) (3.3)
(если частоты есть) (3.3)
где n - число единиц в совокупности.
Численное значение медианы интервального ряда определяют по накопленным частотам в дискретном вариационном ряду. Для этого сначала следует указать интервал нахождения медианы в интервальном ряду распределения. Медианным называют первый интервал, где сумма накопленных частот превышает половину наблюдений от общего числа всех наблюдений.
Численное значение медианы обычно определяют по формуле (3.4)
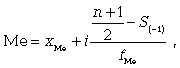 (3.4)
(3.4)
где xМе - нижняя граница медианного интервала; iМе - величина интервала; SМе-1 - накопленная частота интервала, которая предшествует медианному; fМе - частота медианного интервала.
Внутри найденного интервала расчет медианы производится также по формуле Ме = xl е, где второй множитель в правой части равенства показывает расположение медианы внутри медианного интервала, а х — длина этого интервала. Медиана делит вариационный ряд пополам по частотам. Определяют еще квартили, которые делят вариационный ряд на 4 равновеликие по вероятности части, и децили, делящие ряд на 10 равновеликих частей.