
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Типовые структуры алгоритмов
|
|
Типовой (или базовой) структурой называют определенный набор блоков и стандартных способов их соединения для выполнения типичных последовательностей действий. В структурном программировании различают три типовых структуры: 1) линейную, 2) разветвляющуюся, 3) циклическую.
1. Линейная структура алгоритма, называемая также последовательной, предполагает, что действия (блоки) выполняются последовательно друг за другом в порядке их записи (следования). В блок-схеме алгоритма линейной структуры могут использоваться только блоки двух типов (не считая блоков начала и конца, которые должны быть у любого алгоритма): блоки расчета и блоки ввода/вывода (рис. 2).
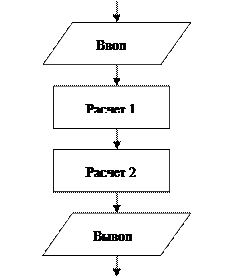
Рис.2. Пример блок-схемы алгоритма линейной структуры
2. Разветвляющаяся структура алгоритма предполагает использование логического блока (блока принятия решения), в котором записывается некоторое условие для проверки. Данный блок имеет два выхода, один из которых помечается словом «Да» (или знаком «+»), другой – словом «Нет» (или знаком «–»).
Условие должно являться выражением логического типа, которое может принимать только одно из двух значений: истина или ложь (true или false). Если при проверке условия оно оказалось истинным, то далее выполнение алгоритма осуществляется по ветке «Да». В противном случае (если условие ложно) выполнение алгоритма происходит по ветке «Нет» (рис.3). Кроме обычного разветвления может использоваться его частный случай, называемый «обход», когда никаких действий на ветку «Нет» не задано (рис.4).

Рис.3. Разветвление Рис.4. Обход
3. Циклическая структура алгоритма предполагает многократное повторение некоторой последовательности действий («цикл» означает «повтор»). Однако «многократно» не значит «бесконечно». Организация цикла, никогда не приводящего к остановке выполнения алгоритма, является нарушением требования его результативности – получения результата за конечное число шагов (см. свойства алгоритма в пункте 2.2).
Любой цикл состоит из двух компонент: 1) условия цикла, которое должно проверяться на каждом шаге цикла и определять момент завершения работы цикла (т.е. выход из цикла), 2) тела цикла, представляющего собой последовательность действий, подлежащих многократному повторению. В зависимости от порядка записи этих компонент различают 2 типа циклов: 1) цикл «с предусловием» (рис. 5), 2) цикл «с постусловием» (рис. 6).
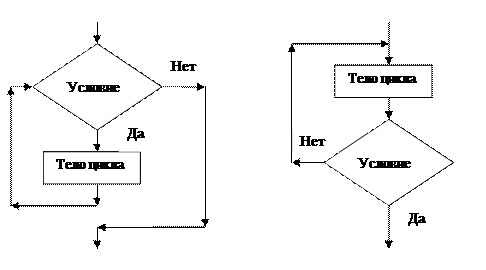
Рис.5. Цикл «с предусловием» Рис.6. Цикл «с постусловием»
По количеству повторений тела цикла различают также 2 типа циклов: 1) цикл с незаданным числом шагов (повторений), 2) цикл с заданным числом шагов.
Особенность цикла с заданным числом шагов в том, что условие цикла в нем не задается в явном виде, а как бы подразумевается. Управление цикла осуществляется через специальную управляющую переменную (как правило, целого типа). В заголовке цикла вместо условия записываются параметры этой управляющей переменной: ее начальное и конечное значения, а также шаг изменения (по умолчанию используется шаг равный 1). Таким образом, уже в заголовке цикла задается определенное количество повторений тела цикла.
Для оформления цикла с заданным числом повторений в блок-схеме используется специальный блок модификации (см. таблицу 2). Для записи такого цикла в программе на языках Бейсик и Паскаль используется оператор For.
В рассмотренном ниже примере (рис. 7) изображен цикл, который всегда (т.е. независимо от действий, заданных до цикла, исходных параметров задачи и содержания тела цикла) будет работать 50 раз. На первом шаге цикла тело выполнится при i=1, на втором шаге – при i=3, на третьем шаге – при i=5 и т.д. Последний раз тело цикла будет выполнено при i=99.
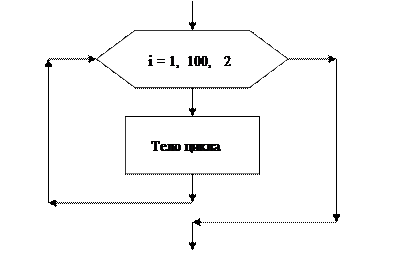
Рис.7. Пример блок-схемы цикла с заданным число повторений
где i – управляющая переменная, 1 – ее начальное значение,
100 – конечное значение, 2 – шаг изменения значения i.