
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Законы излучения
|
|
Рассмотрим две непрерывные поверхности, расстояние между которыми мало по сравнению с их размерами (рис.). Поглощательную способность поверхности 1 обозначим а1, а поглощательную способность абсолютно черной поверхности (0) через а0 =1. Поместим между поверхностями абсолютно прозрачный экран лишь для лучей длиной волны λ. Остальное излучение экран полностью отражает. Температуры экрана и поверхностей равномерны и одинаковы, т.е. они находятся в температурном равновесии.
Плотность излучения от поверхности 0 → 1 обусловлено только собственным излучением поверхности 0 и равно Еλ о. Плотность излучения от поверхности 1 → 0 складывается из собственного излучения поверхности 1 и отраженного ею излучения поверхности 0 и равно Еλ 1+(1 – аλ ) Еλ о. Поскольку система находится в тепловом равновесии, то
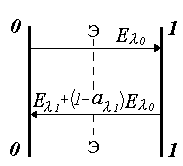
Еλ о= Еλ 1+(1 – аλ ) Еλ о.
Из уравнения  , или
, или  .
.
Отношение плотности излучения тела к его поглощательной способности при данной температуре и длине волны есть величина постоянная.
Следствия из закона Кирхгофа:
§ Так как длина волны была выбрана произвольно и поглощательная способность тела не может быть больше единицы, то при любой длине волны плотность излучения абсолютно черного тела больше, чем любого другого, находящегося при этой же температуре.
§ Так как свойства поверхности 1 не оговаривались, то равенство (3.19) справедливо для всех других поверхностей с той же температурой:
 .
.
Законы Планка и Вина
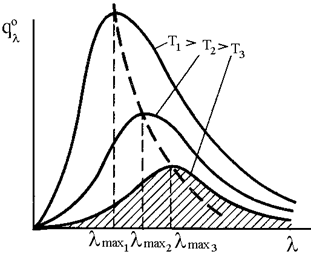
Спектральное распределение плотности потока (Вт/м3) полусферического излучения абсолютно черного тела определяется законом Планка:  , где с1 и с2 – константы. На рис. представлено спектральное распределение плотности потока полусферического излучения абсолютно черного тела при фиксированных температурах.
, где с1 и с2 – константы. На рис. представлено спектральное распределение плотности потока полусферического излучения абсолютно черного тела при фиксированных температурах.
Как видно из графика, с увеличением температуры абсолютно черного тела максимум излучаемой энергии смещается в область более коротких длин волн. Штриховая линия, проходящая через точки максимумов изотерм, соответствует закону смещения Вина, согласно которому
λ maxT = 2897, 8 мкм ·K.
Закон Стефана–Больцмана
Зависимость интегральной сферической плотности излучения абсолютно черного тела от температуры была получена экспериментально И. Стефаном (1879 г.) и на основании термодинамики Л. Больцманом (1884 г.).
 ,
,
где σ о = 5.7 · 10-8 Вт/м2·К4 – коэффициент излучения абсолютно черного тела.
Эта формула является основной при всех расчетах лучистого теплообмена. Поскольку величина σ о мала, а Т4 высока, используют формулу:
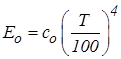 ,
,
где со = 5.7 Вт/м2·К4 – приведенный коэффициент излучения абсолютно черного тела.
Излучение реальных тел. Серое тело
Коэффициент поглощения реальных тел зависит от их природы и состояния поверхности: степени шероховатости, наличия окисных пленок, загрязнений и др. Монохроматический коэффициент поглощения всех реальных тел (твердых, жидких, газообразных) неодинаков для волн различных длин.
Если поглощательная способность aα является величиной переменной, то в соответствии с законом Кирхгофа степень черноты el также изменяется с изменением длины волны l.
Излучение тела, степень черноты которого изменяется в зависимости от длины волны, называется селективным. Наибольшей селективностью обладают газы, наименьшей – твердые диэлектрики с шероховатой поверхностью.
Излучение реальных тел не является идеально диффузным, поэтому яркость лучей, уходящих с поверхности под большими углами к нормали, не остается постоянной (рис.).
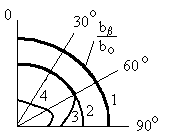
bb – b = f(b), где b – яркость, bо – яркость излучения абсолютно черного тела.
Чтобы облегчить технические расчеты, вводят понятие о сером теле.
Серым называется такое тело, яркость которого одинакова во всех направлениях, а степень черноты постоянна.
 .
.
Реальные тела в технических расчетах рассматриваются как серые. В этом случае можно считать, что поглощательная способность тела равна его степени черноты (а = e).
Теплообмен между серыми телами в лучепрозрачной среде
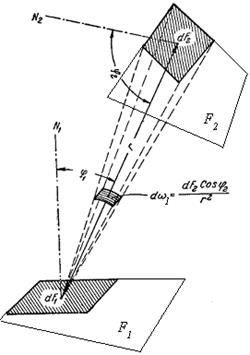
Простейший случай – теплообмен между двумя параллельными абсолютно черными поверхностями. Расстояние между пластинами мало по сравнению с их размерами.
Все излучение одной поверхности полностью поглощается второй, т.к. ао=1. Результирующий поток, уходящий через более холодную поверхность, равен:
 .
.
При теплообмене серых поверхностей, произвольно расположенных в пространстве, задача осложняется тем, что:
1) не все излучение одной из поверхностей может попадать на вторую;
2) не все излучение, попавшее на поверхность, ею поглощается.
Определим, какая доля лучистого потока, уходящего с поверхности F1, попадает на поверхность F2. Согласно закону Ламберта, лучистый поток
 .
.
Так как пространственный угол
 , то
, то
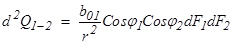 .
.
Чтобы найти лучистый поток Q1-2 , последнее выражение проинтегрируем:

Полный полусферический поток с поверхности F1 на поверхность F2, в соответствии с формулой
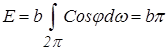 , будет
, будет
 .
.
Разделим выражение (3.20) на (3.21), получим
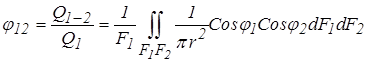 .
.
Величина j12 показывает, какая часть лучистого полусферического потока, уходящего с поверхности F1, попадает на поверхность F2 и называется угловым коэффициентом. Это чисто геометрическая характеристика. Аналогично
 .
.
Вычисление j12 и j21 по этим формулам для многих практических задач представляет большие математические трудности, поэтому во многих случаях j находят методом Г. Л. Поляка, основанном на их некоторых свойствах:
§ свойство взаимности
Сравнивая последние выражения, получим 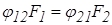 .
.
§ свойство замыкаемости
Рассмотрим замкнутую систему абсолютно черных тел (рис.).

Рассмотрим замкнутую систему абсолютно черных тел.
С поверхности 1 излучение попадает на окружающие поверхности 2–4 и частично на самое себя (если 1 вогнутое), поэтому
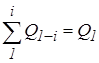 .
.
Разделим на Q1, получим
 .
.
Свойство замыкаемости: сумма угловых коэффициентов для замкнутой системы равна единице.
Определим угловые коэффициенты для некоторых случаев, возможных на практике. Системы двух тел изображены на рис.
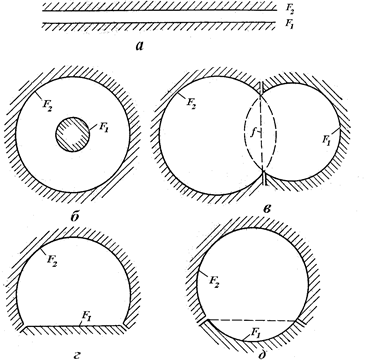
Как видно, таких систем имеется несколько:
а) две большие плоские поверхности, расположенные на небольшом расстоянии одна от другой, 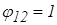 и
и 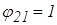 ;
;
б) две концентрические сферические поверхности или два круглых коаксиальных бесконечно длинных цилиндра (тело 1 внутри тела 2):
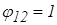 и
и 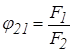 ;
;
в) внутренние поверхности двух полых сфер, пересекающихся между собой:
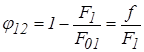
и
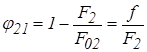 ,
,
где F1 и F2 – поверхности, находящиеся в состоянии лучистого теплообмена;
F01 и F02 – полные поверхности пересекающихся сфер;
f – площадь круга, краями которого является линия пересечения поверхностей F01 и F02;
г) внутренняя поверхность шарового сегмента и плоская круглая поверхность, являющаяся основанием сегмента (F1 – плоская поверхность, а F2 – вогнутая),
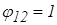 и
и 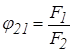 .
.
Этот случай получается из предыдущего при F1 = f;
д) две поверхности, составляющие вместе сферическую полость, контуры их могут быть произвольной формы:
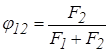 и
и  .
.
Замкнутая система из двух серых тел. Понятие эффективного теплового потока
Рассмотрим теплообмен в замкнутых системах. На тело падает лучистый поток Qпад, который исходит от другого тела, а если тело имеет вогнутости, то и от него самого

Поверхность тела из падающего на нее лучистого потока поглощает тепло Qпогл = а · Qпад, а остальной поток тепла отражает обратно Qотр = Qпад – Qпогл.
Результирующий тепловой поток окончательно ушедший в тепло равен:
 . (3.24)
. (3.24)
Для непрозрачной поверхности, а+r =1, поэтому
 .
.
После подстановки в уравнение 3.24 получим  или
или  . Сумму отраженного лучистого потока и собственного излучения называют эффективным излучением и обозначают
. Сумму отраженного лучистого потока и собственного излучения называют эффективным излучением и обозначают 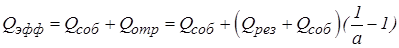 . Учитывая, что для серой поверхности
. Учитывая, что для серой поверхности  , e = а, получим
, e = а, получим
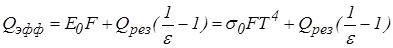 .
.
Если собственное излучение больше поглощенного, то результирующий тепловой поток будет отрицателен.
Рассмотрим теплообмен между двумя произвольными серыми поверхностями 1 и 2, образующими замкнутую систему. Т1 > Т2 – температуры равномерные. Найдем Qрез1-2 .
Поскольку система замкнута, весь эффективный лучистый поток, уходящий с поверхности 1, распределяется между поверхностями 1 и 2. Часть, падающая на поверхность 2, определяется угловым коэффициентом j12, а на поверхность 1 – j21. Следовательно, результирующий поток равен:
 ,
,
или
 . (3.25)
. (3.25)
Из закона сохранения энергии 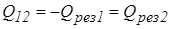 , а вследствие свойства взаимности
, а вследствие свойства взаимности 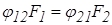 . Алгебраически преобразовав уравнение (3.25), получим
. Алгебраически преобразовав уравнение (3.25), получим

или
 ,
,
где e12 – приведенная степень черноты,
s12 – приведенный коэффициент излучения.
Для схемы, приведенной на рис. 3.19 (а), 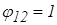 и
и 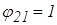 ; F1 = F2;
; F1 = F2;
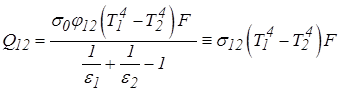 .
.
Для схемы, приведенной на рис. 3.19 (б), 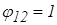 и
и 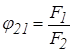 ,
,
 .
.
Излучение газов и паров
Все газы и пары обладают способностью поглощать и излучать лучистую энергию. Излучательная способность двухатомных газов незначительна – их принимают лучепрозрачными. Трехатомные (и более) газы обладают значительной селективной поглощательной и излучательной способностью (рис.).
Наибольший интерес представляют СО2 и Н2О -пар, входящие в состав продуктов сгорания топлива (дым). Энергия излучения СО2 и Н2О зависит от парциального давления газа (р, Па), толщины газового слоя (S, м) и температуры:
 , Вт/м2;
, Вт/м2;
 , Вт/м2.
, Вт/м2.

Для технических расчетов эта формула неудобна, поэтому используют формулы, в которых температура в четвертой степени. Необходимая поправка вводится в общую степень черноты газа – e, которая также учитывает зависимость интенсивности излучения от длины волны  .
.
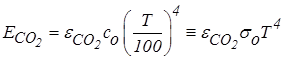 ;
;
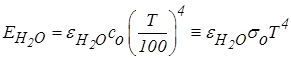 .
.
Излучательная способность газа (ЕГ), содержащего СО2 и Н2О, определяется по формуле:
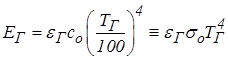 ;
;
 ,
,
где ξ – поправочный коэффициент, который находят из графика 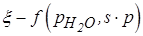 , р – парциальное давление, s – толщина слоя;
, р – парциальное давление, s – толщина слоя;
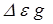 – поправка, учитывающая наложение полос излучения СО2 и Н2О при их совместном пребывании в излучающем пространстве, определяется из графика.
– поправка, учитывающая наложение полос излучения СО2 и Н2О при их совместном пребывании в излучающем пространстве, определяется из графика.
При обычных соотношениях компонентов, которые наблюдаются в дымовых газах, 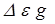 ~ 2÷ 4 %. Ее нужно учитывать при очень точных расчетах и при больших значениях Ро ·S,
~ 2÷ 4 %. Ее нужно учитывать при очень точных расчетах и при больших значениях Ро ·S,
где Ро – общее давление газа;
S – эффективная длина луча,  ;
;
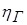 – коэффициент эффективности газового излучения, характеризующий долю излучения, достигающую стенок;
– коэффициент эффективности газового излучения, характеризующий долю излучения, достигающую стенок;
V – объем, заполненный газом;
F –площадь всех стенок, ограничивающих этот объем.
Теплообмен в системе «серый газ – замкнутая серая оболочка»
Рассмотрим замкнутую серую оболочку с равномерной температурой Т1 и степенью черноты e1. Площадь внутренней поверхности оболочки – F1. Внутри оболочки находится серый газ с равномерной температурой ТГ и степенью черноты – eГ. Найдем тепловой поток от газа к оболочке QГ-1 .
Все эффективное излучение оболочки попадает в газ, но только часть его, пропорциональная его поглощательной способности аГ, поглощается. Так как для серого газа аГ = eГ, то, в соответствии с формулой 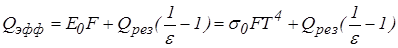 , получим
, получим
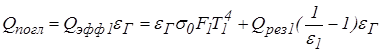 .
.
Результирующий поток, отдаваемый газом оболочке, равен разности между собственным и поглощенным излучением:
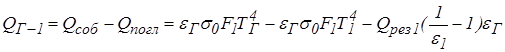 .
.
Учитывая, что результирующий поток, отдаваемый газом, равен результирующему потоку, проходящему через оболочку (QГ-1 = Qрез1), и, проведя простые преобразования формулы (3.28), получим
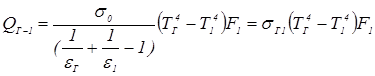 .
.
Это формула Нуссельта. Её применяют для расчета лучистого потока от газа к рекуперативным трубам и регенеративной насадке.
Серый газ в замкнутой системе, состоящей из двух поверхностей
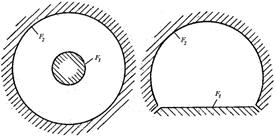
| Две серые поверхности, из которых 1 не вогнутая (рис.), а 2 – вогнутая и адиабатная, образуют замкнутую систему, заполненную серым газом. Температуры газа и поверхности 1 известны. Определим тепловой поток от газа к серой оболочке 1 (QГ-1 -?). |
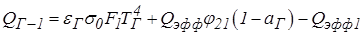 ;
;
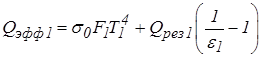 .
.
Qэфф2 определить нельзя, т. к. неизвестна Т2.
Воспользуемся тем, что поверхность 2 адиабатная и ее эффективное излучение равно излучению падающего потока, т.е. Qэфф2 = Qпад2.
 ,
,
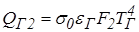 ,
,
 .
.
Из уравнения 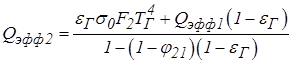 .
.
Подставляя значения Qэфф1 и Qэфф2 в уравнение (3.29), получим:
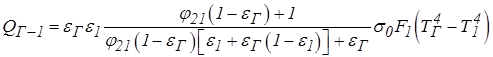 ,
,
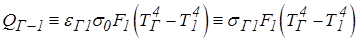 .
.
где sГ1=sпр=sГКМ – приведенный коэффициент излучения газа, кладки на металл, 1 – нагреваемый металл, 2 – кладка печи.
Это формула Тимофеева. Её применяют для расчета теплообмена в промышленных печах и топках котлов.
Коэффициент развития кладки w = 1/j21.
|